Добавить материал

и получить 10 документов
и свидетельство СМИ

Изображение пользователя Рыбинок Екатерина Валерьевна Рыбинок Екатерина Валерьевна

2-сабак Сан тiзбегi. Мат индукция әдісі

  • docx
  • 12.05.2020
Публикация в СМИ для учителей

Публикация в СМИ для учителей

Бесплатное участие. Свидетельство СМИ сразу.
Мгновенные 10 документов в портфолио.

Добавить материал
Иконка файла материала 2-сабак Сан тiзбегi. Мат индукция әдісі.docx

Ұзақмерзімдіжоспарбөлімі: Тізбектер

Мектеп:

Күні:

Мұғалімнің аты-жөні:

Сынып:9

Қатысқандарсаны:

Қатыспағандар саны:

Сабақтақырыбы

Сандар тізбегі, оның берілу тәсілдері және қасиеттері

Осысабақтақолжеткізілетіноқумақсаттары (оқубағдарламасынасілтеме)

9.2.3.1сандар тізбегі туралы түсінік болу;

9.2.3.2тізбектің n-ші мүшесін табу, мысалы:;

9.2.3.3математикалық индукция әдісін білу және қолдану

Сабақмақсаттары

Оқушылар білетін болады:

·                    негізгі ұғымдарды  («тізбек», «тізбектің n-мүшесі», индукция және дедукция, индукция базасы);

·                    тізбек элементтерін оның n-мүшесі формуласының көмегімен табуды және керісінше, берілген формула бойынша тізбектің n-мүшесін анықтауды;

·                    математикалық индукция әдісін;

·                    алған білімдерін есеп шығаруда қолдануды.

Жетістіккритерийлері

Оқушы:

·                    сандық тізбек анықтамасы мен оның берілу тәсілдерін біледі;

·                    тізбекті аналитикалық түрде, яғни формуламен бере алады;

·                    аналитикалық түрде берілген тізбектің кез келген мүшесін таба алады;

·                    математикалық индукция әдісінің мәнін түсінеді және оны тізбектер үшін қолданады.

Тілдікмақсаттар

Оқушылар:

- теориялық материалды ауызша қайталауда сөйлемдерді толықтырады;

- индукция түрлері туралы талқылау жүргізеді.

Пәнгетән лексика мен терминология:

Тізбек, натурал жиында анықталған функция, тізбектің бірінші мүшесі және n-ші мүшесі, тізбектің берілу тәсілдері, аналитикалық, сөзбен және рекурренттік тәсілдер, заңдылық; индукция базасы, математикалық индукция әдісі.

Диалог пен жазу үшін пайдалы сөздер мен тіркестер:

- Тізбек ... түрде беріледі.

- Математикалық индукция принципі ...

Құндылықтардыдарыту

Оқи алу дағдысы, өздігімен ақпарат іздестіру, жағдайды талдау, жаңа жағдайларға бейімделу, мәселелерді қоя және оларды шеше білу, топта, жұпта жұмыс жасау, өз уақытын тиімді ұйымдастыра білу, өз жұмысының сапасына жауап беру.

Аталған құндылықтар сабақта жоспарланған жұмыстар арқылы орындалады.

Пәнаралықбайланыстар

Жаратылыстану ғылымдары. Фибоначчи сандары.

Бастапқы білім

Функция, анықталу облысы, мәндер облысы, функцияның берілу тәсілдері,  тізбек, тізбектердің берілу түрлері.

Сабақбарысы

Сабақтыңжоспарланғанкезеңдері

Сабақтағыжоспарланғаніс-әрекет

 

Ресурстар

Сабақ

басы

0-8 мин

 

1. Ұйымдастыру кезеңі. Оқуға ынталандыру.

Оқушыларға төмендегі сұрақтарды негізге ала отырып, өткен сабақтағы негізгі ұғымдарды жұптарда қайталауға ұсыныс жасаңыз:

- Сандық тізбек дегеніміз не?

- Сандық тізбек қалай беріледі?

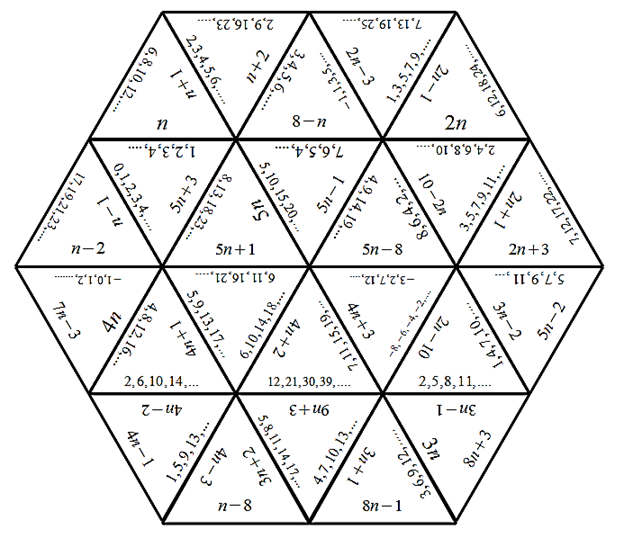
- Сандық тізбекті  формуласымен құрастыру үшін не белгілі болуы қажет? Мұндай берілу тәсілі қалай аталады?

Ширату. «Тарсия».

Оқушыларға 4 оқушыдан құралатын топтарға бірігіп, тізбектің n-мүшесінің формуласы мен оның элементтерін сәйкестендіруге арналған «Тарсияны» шешу жұмысын тапсырыңыз.

 

 

 

 

 

 

 

 

 

 

 

 

Қосымша 1

 

Ортасы

9 – 18 мин

 

 

 

 

 

 

 

 

 

 

 

 

 

 

19- 26 мин

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

27 - 31 мин

 

 

 

 

 

 

 

 

32 - 38 мин

Қайталау. Өздік жұмыс. Сараланған тапсырмалар. 

Тапсырма оқып-үйренген ұғымдарды нақтылап, бекітуге бағытталған.

Оқушыларға «өспелі/кемімелі тізбек», «тізбектің ең үлкен/ең кіші мүшесі» мағыналарын түсінуге бағытталған тапсырмалар топтамасынөздігімен шешу ұсынылады. Сонымен қатар, оқушылар бұл тізбектерді оқып-үйрене отырып, жаңіа терминдер туралы қорытынды жасаулары керек. Мұғалім оқушыларға дұрыс бағыт-бағдар көрсетіп, қажет болған жағдайда жеке көмек көрсетеді.

Сонымен қатар оқушылар тізбектің алғашқы мүшелері белгілі болғанда n-мүшесінің формуласын табуға бағытталған тапсырмалар орындайды. Осыдан кейін мұғалім шешімдерін тексеру үшін оқушыларды қиындық деңгейіне байланысты топтарға біріктіруді ұйымдастырады.

 

Жаңа тақырып. Математикалық индукция әдісі. Жалпы сыныппен жұмыс.

Теориялық материал мен сызбаға сүйене отырып жаңа ұғымдарды енгізу:

Оқушылармен бірігіп математикалық индукция әдісінің алгоритмін талқылау. Мысалды толығымен қарастыру.

 

Тәжірибелік жұмыс.

Оқушыларға 4-қосымшаның жеткіліксіз пунктілерін толтыруды ұсыныңыз. Оқушылар нұсқаулар көмегімен тұжырымдаманы математикалық индукция көмегімен дәлелдеп, оның мағынасы мен іс-әрекет алгоритмін бекітеді.

 

 

 

 

Жаттығу тапсырмалары. Жұптардағы жұмыс.

Оқушыларды жұптарға біріктіріңіз. 5-қосымшаның тапсырмаларын алдымен өздігімен орындап, одан кейін серігімен салыстыруды ұсыныңыз.

Уақытпен шектеңіз. Қиындық туғызған тапсырмаларды оқушылармен бірігіп талқылаңыздар.

 

 

 

Қосымша 2

 

 

А.Е.Абылкасымова и др. Алгебра. Учебник для 9 класса общеобр.школ. Алматы:Мектеп,2019г

 

 

 

 

Қосымша 3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Қосымша 4

М.Л. Галицкий, А.М. Гольдман, Л.И.Звавич,  «Сборник задач по алгебре 8-9» М.:Просвещение 2001г.

 

 

Қосымша 5

Сабақтың соңы

39 - 40 мин

Сабақ соңында оқушылар келесі сұрақтарға жауап беру арқылы ауызшарефлексия жүргізеді:

- не білдім, не үйрендім?

- не түсініксіз болып қалды?

- немен жұмыс жасау керек?

 

Мұғалім үй тапсырмасын орындау бойынша нұсқаулар береді.

 

 

 

 

 

 

Қосымша 6

Саралау –оқушыларғақалайкөбірекқолдаукөрсетудіжоспарлайсыз? Қабілетіжоғарыоқушыларғақандайміндетқоюдыжоспарлапотырсыз?

Бағалау – оқушылардыңматериалдымеңгерудеңгейінқалайтексерудіжоспарлайсыз?

Денсаулықжәнеқауіпсіздіктехникасыныңсақталуы

Мұғалім оқушыларға есеп шығару барысында жеке көмек көрсетеді. Тапсырмалар қиындық деңгейінің өсу ретімен таңдалған.

1. Жалпы сыныппен әңгімелесу кезінде мұғалім оқушылардың жаңа терминдер мен ұғымдарды түсінуін, жаңа материалды саналы түрде ұғынуын бақылайды;

2. Жұптарда өзара бағалау жүзеге асады;

3. Сабақ соңында оқушылар сабақ мақсаттарына жету бойынша рефлексия жасайды (ауызша).

Үзіліс уақытында оқу кабинетін желдетіп алу керек. Парталар мен орындықтардың дұрыс орналасуына назар  аудару керек.

 

 

 

1-қосымша. Ширату

2-қосымша.

А деңгейі

№12.4.Келесі алғашқы мүшелері белгілі (an)тізбегінің n-мүшесінің формуласын табыңыз:

1)      2; 4; 6; 8; 10; 12; 14;

2)     

3)      1; 2; 4; 8; 16; 32;

4)     

5)     

№12.7.Келесі тізбектердің қайсысы:

а) өспелі;    б) кемімелі;   в) өспелі де, кемімелі де емес:

1)    -1; -5; -9; -13; -17;

2) 

3)  

Жауаптары: №12.4.  1) 2n; 2) ; 3) ; 4) . №12.7.1) кемімелі; 2) мен 3) өспелі.

 

В деңгейі

№12.9. n-мүшесінің қай формулалары: а) өспелі; б) кемімелі сан тізбегін береді:

1)     

2)     

3)     

№ 12.15.  Төмендегі формуламен берілген (an) сандық тізбегінің кемімелі екендігін дәлелдеңіз:

1)

2)

3)

№ 12.17. n-мүшесінің формуласымен берілген тізбектің ең кіші мүшесін табыңыз:

1)

2)

3)

Жауаптары: №12.9. 1) өспелі; 2) кемімелі;  3) өспелі.  № 12.17.  1) -36;  2) -40;  3) 4.   

С деңгейі

№ 12.18. Сан тізбегінің, мүмкін болса, ең кіші және ең үлкен мүшесін табыңыз:

1)

2)

№ 12.19. (an) сандық тізбегінің n-ші мүшесінің формуласын табыңыз, егер оның келесідей алғашқы мүшелері белгілі болса:

1)        0; 7; 26; 63; 124; 215;

2)        1; 7; 31; 127; 511;

3)       

№ 12.20. Сан тізбегін шектелгендікке зерттеңіз:

1)     

2)     

Жауаптары:№ 12.18. 1) ең үлкені с1=-1,5;  2) ең үлкеніс1=6 . № 12.19. 1) ; 2) ; 3)  .

 

3-қосымша. Математикалық индукция әдісі. Теория.

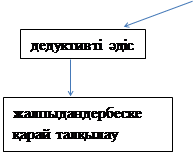
Дедуктивті және индуктивті әдіс

Кез келген математикалық зерттеудің негізінде дедуктивті және индуктивті әдістер жатады. Пайымдаулардың дедуктивті әдісі – бұл жалпыдан дербеске қарай пайымдау, яғни бастапқыдағы жалпы нәтижеден соңындағы дербес нәтижеге қол жеткізетін пайымдау түрі.

Индукция сөзі жетелеу деген мағынаны білдіреді, ал индуктивті деп, қадағалаунәтижесін, тәжірибені негізге ала отырып жасалған, яғни дербестен жалпыға қарай тұжырымдау жолымен алынған қорытындыларды айтады.

Толық және толық емес индукция

Математикалық индукция әдісін ілгерілеумен салыстыруға болады. Біз төменнен бастаймыз, логикалық ойлау нәтижесінде жоғарыға келеміз. Адам әрқашанда ілгерілеуге, өз ойын логикалық тұрғыдан дамытуға ұмтылған, демек, табиғаттың өзі оған индуктивті дамуды жазып қойған.

Толық индукция

4≤n≤20 аралығындағы әрбірn жұп натурал санын екі жай санның қосындысы түрінде  жазуға болатынын көрсету керек болсын. Ол үшін сондай барлық сандарды алып, сәйкес жіктеулерді жазып шығамыз:

                  4=2+2; 6=3+3; 8=5+3; 10=7+3; 12=7+5;

                  14=7+7; 16=11+5; 18=13+5; 20=13+7.

Бізді қызықтыратын әрбір санекі жай санның қосындысы түрінде  жазылады.

Толық индукцияның мәнісі, ол жалпы тұжырым шектеулі мүмкін жағдайлардың әрбірі үшін жеке дәлелденетінінде.

Толық емес индукция

Кейде жалпы нәтижені барлық жағдайларды қарастырмай-ақ, өте көп дербес жағдайларды қарастырғаннан кейін болжау мүмкін болады (толық емес индукция десе де болады). Алайда, толық емес индукциямен алынған нәтиже барлық дербес жағдайларды қамтитын дәл математикалық тұжырымдар көмегімен дәлелденбегенше, тек гипотеза болып қалады.

Математикалық индукция әдісі

Кез келген натурал n саны үшін қандай да бір тұжырымның ақиқаттығын дәлелдеу керек болсын. Бұл тұжырымды n–нің әрбір мәні үшін тікелей тексеру мүмкін емес, өйткені натурал сандар жиыны шексіз. Бұл тұжырымды дәлелдеу үшін:

  1. оның n=1 үшін ақиқаттығын тексеру керек.
  2. k-ның кез келген натурал мәнінде тұжырымның дұрыстығын болжайды.
  3. n=k+1 үшін тұжырымның ақиқаттығын дәлелдейді.
  4. Text Box: Математикалық зерттеу сонда тұжырым барлық n үшін ақиқат деп саналады.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


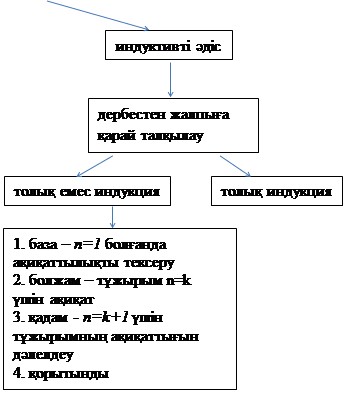Мысал: Тепе-теңдікті дәлелдеңіз:

.

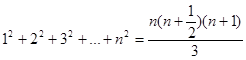1.      [ИНДУКЦИЯ БАЗАСЫ]n=1 үшін бұл орындалуын тексерейік:

 

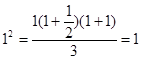
n=2 үшін:

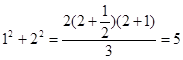
2.[БОЛЖАМ] Тепе-теңдікn=k үшін ақиқат деп болжайық, яғни

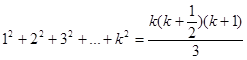
3.[ҚАДАМ] Индукция қадамы осы тепе-теңдікті n=k+1 үшін тексергенге сәйкес келеді, яғни келесіні дәлелдеу керек

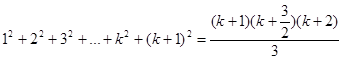
4.[ҚОРЫТЫНДЫ] Тепе-теңдік кез келген n үшін ақиқат.

 

4-қосымша.

Тәжірибелік жұмыс

Тапсырма: Алғашқы n натурал сандардың кубтарының қосындысы  тең екенін дәлелдеңіз.

  1. n=1 үшін ақиқаттықты тексереміз:

n=2 үшін:

…………………………………………………………………………………..

  1. k-ның кез келген натурал мәні үшін тұжырым ақиқат деп болжайық, яғни келесі ақиқат:

  1. n=k+1 үшін тұжырымның ақиқаттығын дәлелдейміз:

 

…………………………………………………………………………………..

…………………………………………………………………………………..

  1. Демек, тұжырым барлық n үшін ақиқат.

5-қосымша.

№18.5. Келесі теңдіктің барлық натурал сандар үшін ақиқаттығын математикалық индукцияәдісімен дәлелдеңіз:

1)      ;

2)      .

№18.7. Барлық натурал сандар үшін математикалық индукцияәдісімен дәлелдеңіз:

1)      өрнегінің 5-ке бөлінетіндігін;

2)      өрнегінің7-ге бөлінетіндігін.

 

6-қосымша. Үй тапсырмасы.

№ 1.  Келесі формуламен берілген (an) сандық тізбегінің өспелі болатындығын дәлелдеңіз:

1)

2)

3)

№2. Тұжырымды математикалық индукция әдісімен дәлелдеңіз:

 түріндегі алғашқы n сандардың қосындысы  тең екендігін дәлелдеңіз.

 

Тізбектер Мектеп: Ширату. «Тарсия». Оқушыларға 4 оқушыдан құралатын топтарға бірігіп, тізбектің n-мүшесінің формуласы мен оның элементтерін сәйкестендіруге арналған «Тарсияны» шешу жұмысын тапсырыңыз Ортасы 9 – 1 8 мин 1 9 - 2 6 мин 2 7 - 31 мин 32 - 38 мин Қайталау Ширату 2 -қосымша . А деңгейі №12 Жауаптары : №12.4. 1) 2 n ; 2) ; 3) ; 4) Сан тізбегін шектелгендікке зерттеңіз : 1) 2) Толық емес индукция Кейде жалпы нәтижені барлық жағдайларды қарастырмай-ақ, өте көп дербес жағдайларды қарастырғаннан кейін болжау мүмкін болады (толық емес индукция десе де болады) ИНДУКЦИ Я БАЗАСЫ ] n =1 үшін бұл орындалуын тексерейік : n =2 үшін : 2 Демек , тұжырым барлық n үшін ақиқат

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также