2.11 Признаки равенства прямоугольных треугольников

Признаки равенства прямоугольных треугольников.

Повторяем теорию.

Признаки равенства прямоугольных треугольников:

1.            (по двум катетам) Если катеты одного прямоугольного треугольника соответственно равны катетам другого треугольника, то такие треугольники равны.

2.            (по катету и прилежащему к нему острому углу) Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого треугольника, то такие треугольники равны.

3.            (по катету и противолежащему углу) Если катет и противолежащий ему угол одного прямоугольного треугольника соответственно равны катету и противолежащему углу другого треугольника, то такие треугольники равны.

4.            (по гипотенузе и острому углу) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие треугольники равны.

5.            (по гипотенузе и катету) Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны.

Проверяем себя.

Т1. Вставьте пропущенное слово:

а) Если катеты одного прямоугольного треугольника соответственно равны                         другого треугольника, то такие треугольники равны.

б)    Если    катет    и    прилежащий    к    нему                               одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.

в)   Если   гипотенуза   и соответственно равны гипотенузе и равны.

одного  прямоугольного  треугольника другого, то такие треугольники

г)   Если   гипотенуза   и   катет   одного   прямоугольного   треугольника

                       гипотенузе и катету другого, то такие треугольники равны.

Ответ: а) катетам; б) острый угол; в) острый угол; острому углу; г) соответственно равны.

Т2. Выберите верное утверждение

а) Прямоугольные треугольники равны, если гипотенуза и угол одного треугольника равны гипотенузе и углу другого треугольника.

б) Прямоугольные треугольники равны, если два угла одного треугольника равны двум углам другого треугольника.

в) Прямоугольные треугольники равны, если гипотенуза и катет одного треугольника равны гипотенузе и катету другого треугольника.

г)   Прямоугольные  треугольники   равны,  если   катет   и   угол   одного треугольника равны катету и углу другого треугольника.

Ответ: в)

Т3. Выберите верное утверждение

1)   Если две стороны одного прямоугольного треугольника соответственно равны двум сторонам другого прямоугольного треугольника, то такие треугольники равны.

2)   В равнобедренном прямоугольном треугольнике медиана, проведенная из вершины прямого угла, образует два равных прямоугольных треугольника.

3)        Если острые углы одного прямоугольного треугольника равны соответственно острым углам другого прямоугольного треугольника, то такие треугольники равны

4)    Если прямоугольные треугольники имеют равные гипотенузы, то они равны.

Ответ: 2.

Решаем задачи.

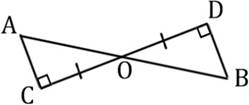
1.     а) Отрезок АВ пересекает отрезок СD в его середине точке О. АС⊥СD, ВD⊥СD, СD=8,2 см, АВ=11,6 см. Найдите ВО.

Ответ: 5,8

б) Отрезок АВ пересекает отрезок СD в

его середине точке О. АС⊥СD, ВD⊥СD, СD=6,6 см, АВ=9,4 см. Найдите ВО.

Ответ: 4,7

в) Отрезок АВ пересекает отрезок СD в его середине точке О. АС⊥СD, ВD⊥СD, СD=8 см, АВ=10 см. Найдите ВО.

Ответ: 5

2. 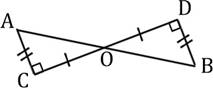    а) В треугольнике АОС, изображенном на рисунке, АС=3, СО=4. Найдите DО.

Ответ: 4

б) В треугольнике АОС, изображенном на рисунке, АС=5, СО=12. Найдите BD.

Ответ: 5

в) В треугольнике АОС, изображенном на рисунке, АС=10, СО=24.

Найдите DО.

Ответ: 24.

3.             а) В треугольнике АВС с прямым углом А и углом В, равным 30°, ВС=10, а в прямоугольном треугольнике КMN гипотенуза КМ=10, прилежащий к ней угол М равен 60°. Найдите МN.

Ответ: 5

б) В треугольнике АВС с прямым углом А и углом В, равным 30°, ВС=16, а в прямоугольном треугольнике КMN гипотенуза КМ=16, прилежащий к ней угол М равен 60°. Найдите МN.

Ответ: 8

в) В треугольнике АВС с прямым углом А и углом В, равным 30°, ВС=12, а в прямоугольном треугольнике КMN гипотенуза КМ=12, прилежащий к ней угол М равен 60°. Найдите МN.

Ответ: 6.

4.                а) Из точки D, лежащей на биссектрисе угла ВАС, опущены перпендикуляры к сторонам АВ и АС. Расстояние от точки D до прямой АС равно 7,4 см, АС=18,6. Найдите длину перпендикуляра, проведенного к стороне АВ.

Ответ: 7,4

б) Из точки D, лежащей на биссектрисе угла ВАС, опущены перпендикуляры к сторонам АВ и АС. Расстояние от точки D до прямой АС равно 3,4 см, АС=8,6. Найдите длину перпендикуляра, проведенного к стороне АВ.

Ответ: 3,4

в) Из точки D, лежащей на биссектрисе угла ВАС, опущены перпендикуляры к сторонам АВ и АС. Расстояние от точки D до прямой АС равно 5,1 см, АС=20,2. Найдите длину перпендикуляра, проведенного к стороне АВ.

Ответ: 5,1

5.            а) ∠АВС=∠АСВ, АК=8 см, МВ=2 см, ВС=6 см. Найдите периметр треугольника АВС.

Ответ: 26

б) ∠АВС=∠АСВ, АК=6 см, МВ=3 см, ВС=5 см.

Найдите периметр треугольника АВС.

Ответ: 23

в) ∠АВС=∠АСВ, АК=10 см, МВ=3 см, ВС=8 см.

Найдите периметр треугольника АВС.

Ответ: 34

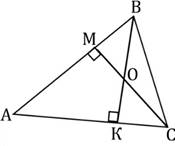
6.              а) По изображению на рисунке найдите СВ, если АВ=10.

Ответ: 10

б) По изображению на рисунке найдите СВ, если АВ=17.

Ответ: 17

в) По изображению на рисунке найдите СВ, если АВ=13.

Ответ: 13

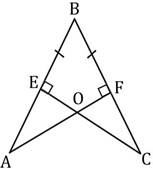
7.  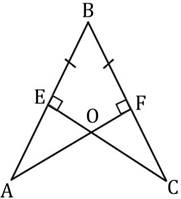          а) По изображению на рисунке найдите СF, если АЕ=4.

Ответ: 4

б) По изображению на рисунке найдите СF, если АЕ=9,5.

Ответ: 9,5

в) По изображению на рисунке найдите СF, если АЕ=14.

Ответ: 14.

Задачи с развернутым ответом.

1.    Биссектриса, проведенная из вершины равнобедренного треугольника, равна 5. Периметр одного из образованных треугольников равен 30. Найдите периметр данного равнобедренного треугольника.

Ответ: 50

Докажите, что если середина высоты треугольника равноудалена от концов стороны, к которой она проведена, то треугольник равнобедренный