2.12 Диагонали и высоты в параллелограмме, ромбе, прямоугольнике, квадрате, трапеции

Диагонали и высоты в параллелограмме, ромбе, прямоугольнике, квадрате, трапеции.

Повторяем теорию

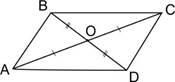Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

AC ⋂ BD = O ,

AO = OC, BO = OD.

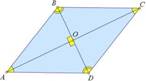Диагонали ромба пересекаются и в точке пересечения делятся пополам.

Диагонали ромба взаимно перпендикулярны. Диагонали ромба являются биссектрисами его углов. AC ⋂ BD = O , AO = OC, BO = OD

𝐴𝐶 ⊥ 𝐵𝐷

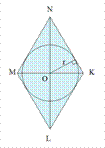AC и BD – биссектрисы.

Точка               пересечения  диагоналей  ромба  является  центром вписанной окружности.

Диагонали               прямоугольника  пересекаются   и   точкой пересечения делятся пополам.

Диагонали прямоугольника равны. AC ⋂ BD = O , AC = BD ,

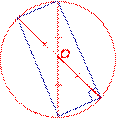AO = OC = BO = OD.

Точка пересечения диагоналей прямоугольника является центром описанной окружности.

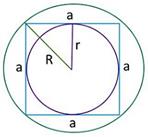Диагонали                  квадрата     пересекаются      и      точкой пересечения делятся пополам.

Диагонали квадрата равны.

Диагонали квадрата взаимно перпендикулярны.

Диагонали               квадрата   являются   биссектрисами   его углов.

Точка пересечения диагоналей квадрата является центром вписанной и описанной окружности.

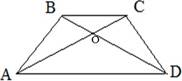
Диагонали трапеции пересекаются. AC ⋂ BD = O.

Если трапеция равнобокая, то ее диагонали равны.

Высота параллелограмма – это перпендикуляр, проведенный из любой точки одной из стороны параллелограмма к прямой, содержащей противоположную сторону.

Из каждой вершины параллелограмма можно провести две высоты.

Высота, проведенная к большей стороне,

имеет меньшую длину, а высота, проведенная к меньшей стороне, имеет большую длину.

Высота                ромба   –    это    перпендикуляр,                 D                                 C

проведенный из любой точки одной из стороны

ромба               к           прямой,          содержащей противоположную сторону.

Из                 каждой    вершины    ромба    можно провести две высоты.                                     A

Высоты ромба равны (DH=DK).

В прямоугольнике каждая сторона является его высотой. В квадрате каждая сторона является его высотой.

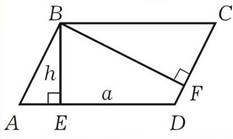
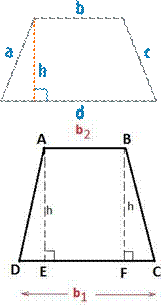
Высотой трапеции называется перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание.

Если трапеция равнобокая, то высоты, проведенные из вершин меньшего основания, отсекают равные прямоугольные треугольники.

∆ ADE = ∆ BCF.

Если в равнобедренной трапеции диагонали перпендикулярны, то высота трапеции равна длине ее средней линии.

Проверяем себя.

Т1. Вставьте пропущенное слово:

а) Диагонали ромба взаимно        . б) Диагонали прямоугольника                                                            . в) Диагонали                                трапеции равны.

г) В ромбе все высоты                                         .

Ответ: а) перпендикулярны; б) равны; в) равнобокой; г) равны.

Т2. Выберите верное утверждение

а) Диагонали параллелограмма являются биссектрисами его углов. б) Диагонали ромба равны.

в) Диагонали параллелограмма точкой пересечения делятся пополам. г) Диагонали трапеции взаимно перпендикулярны.

Ответ: в).

Т3. Выберите верные утверждения:

а) Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

б) Если в выпуклом четырехугольнике диагональ делит его на два равных треугольника, то он является параллелограммом.

в) В трапеции диагональ делит её на два равных треугольника.

г) Четырехугольник, у которого диагонали взаимно перпендикулярны и точкой пересечения делятся пополам, является ромбом.

Ответ: а), г).

Решаем задачи.

1.     а) Биссектриса одного из углов прямоугольника делит сторону прямоугольника пополам. Найдите периметр прямоугольника, если его меньшая сторона равна 12.

Ответ: 72

б) Биссектриса одного из углов прямоугольника делит сторону прямоугольника пополам. Найдите периметр прямоугольника, если его меньшая сторона равна 15.

Ответ: 90

в) Биссектриса одного из углов прямоугольника делит сторону прямоугольника пополам. Найдите периметр прямоугольника, если его меньшая сторона равна 22.

Ответ: 132

2.     а) В прямоугольнике точка пересечения диагоналей отстоит от меньшей стороны на 12, а от большей стороны на 15. Найдите периметр прямоугольника.

Ответ: 108

б) В прямоугольнике точка пересечения диагоналей отстоит от меньшей стороны на 7, а от большей стороны на 10. Найдите периметр прямоугольника.

Ответ: 68

в) В прямоугольнике точка пересечения диагоналей отстоит от меньшей стороны на 3, а от большей стороны на 9. Найдите периметр прямоугольника.

Ответ: 48

3.                 а) Основания трапеции равны 11 и 18. Диагональ трапеции делит среднюю линию на два отрезка. Найдите длину большего из них.

Ответ: 9

б) Основания трапеции равны 4 и 10. Диагональ трапеции делит среднюю линию на два отрезка. Найдите длину большего из них.

Ответ: 5

в) Основания трапеции равны 6 и 12. Диагональ трапеции делит среднюю линию на два отрезка. Найдите длину большего из них.

Ответ: 6

4.               а) Найдите периметр квадрата, если расстояние от точки пересечения диагоналей квадрата до его стороны 12.

Ответ: 96

б) Найдите периметр квадрата, если расстояние от точки пересечения диагоналей квадрата до его стороны 10.

Ответ: 80

в) Найдите периметр квадрата, если расстояние от точки пересечения диагоналей квадрата до его стороны 15.

Ответ: 120

5.                а) Сторона ромба равна 4, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.

Ответ: 2

б) Сторона ромба равна 7, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.

Ответ: 3,5

в) Сторона ромба равна 12, а один из углов этого ромба равен 150°.

Найдите высоту этого ромба.

Ответ: 6

6.                а) Сторона ромба равна 28, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?

Ответ: 14; 14

б) Сторона ромба равна 34, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?

Ответ: 17; 17

в) Сторона ромба равна 40, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?

Ответ: 20; 20

7.                  а) В равнобедренной трапеции диагональ является биссектрисой острого угла. Периметр трапеции равен 14 см, а большее основание - 5 см. Найдите меньшее основание.

Ответ: 3

б) В равнобедренной трапеции диагональ является биссектрисой острого угла. Периметр трапеции равен 23 см, а большее основание - 8 см. Найдите меньшее основание.

Ответ: 5.

в) В равнобедренной трапеции диагональ является биссектрисой острого угла. Периметр трапеции равен 36 см, а большее основание – 12 см. Найдите меньшее основание.

Ответ: 8

Задачи с развернутым ответом.

1.     В трапеции ABCD боковые сторон AB и CD равны, CH – высота, проведенная к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.

Ответ: 12

2.     Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба 76. Найдите все углы ромба.

Ответ: 60°,60°,120°,120°