2.14 ПР Углы. Линии в треугольнике, четырехугольнике и окружности

Проверочная работа по теме «Углы. Линии в треугольнике, четырехугольнике и окружности».

В каждом варианте предлагаются по 3 теоретических вопроса и 7 задач базового уровня сложности, по типу предлагаемых на ОГЭ по математике. Также представлены 2 дополнительные, более сложные задачи.

Тренировочный вариант.

1.      Вставьте пропущенное слово:

а) Два угла называются                                , если стороны одного угла являются продолжениями сторон другого.

б) В равнобедренном треугольнике углы                                     равны. в) Биссектрисы смежных углов взаимно                                          .

г) Если две параллельные прямые пересечены секущей, то                    углы равны,                                                         углы равны, а сумма                                       углов равна 180°.

Ответ: а) вертикальными; б) при основании; в) перпендикулярны; г) накрест лежащие, соответственные; односторонних.

2.      Выберите верное утверждение:

а) Если два угла равны, то они вертикальные.

б)    Любой      вписанный      угол     окружности       равен     половине      любого      её центрального угла.

в) Все углы ромба- острые.

г) Внешний угол треугольника равен сумме двух углов, не смежных с ним.

Ответ: г)

3.      Выберите верное утверждение:

1)  Медиана всегда делит пополам один из углов треугольника.

2)  Высота треугольника может находиться вне треугольника.

3)  Существует треугольник, стороны которого равны 1, 2, 3.

4)  Любой равнобедренный треугольник является равносторонним.

Ответ: 2.

4.      Один из углов, образованных при пересечении двух прямых в 4 раза больше другого. Найдите эти углы. Ответ дайте в градусах. Ответ: 36 и 144

5. 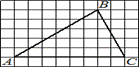     В треугольнике ABC угол C равен 101°. Найдите внешний угол при вершине C. Ответ дайте в градусах . Ответ. 79.

6.   На клетчатой бумаге размером клетки 1x1 изображен треугольник ABC. Найдите длину средней линии треугольника, параллельной стороне AC. Ответ: 4.

7.   Две прямые пересечены третьей. Один из накрест лежащих углов равен 61°, другой-59°. На сколько градусов нужно увеличить меньший угол, чтобы прямые стали параллельными? Ответ: 2

8.   В прямоугольном треугольнике один из острых углов равен 37°. Найдите больший из углов, на которые высота, проведенная к гипотенузе, делит прямой угол. Ответ: 53

9. 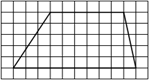  В треугольнике АВС провели среднюю линию DЕ, параллельную стороне АВ. Периметр треугольника СDЕ равен 27. Найдите периметр треугольника АВС. Ответ: 54.

10.        На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите длину ее средней линии. Ответ:8

Вариант 1

1.    Какое из следующих утверждений верно?

1)    В равностороннем треугольнике все медианы равны.

2)    Смежные углы всегда равны.

3)    Боковые стороны любой трапеции равны.

2.     Какое из следующих утверждений верно?

1)   Если в параллелограмме диагонали равны и перпендикулярны, то он является квадратом.

2)   В параллелограмме смежные стороны равны.

3)   Средняя линия трапеции равна полусумме ее оснований.

1.   Какое из следующих утверждений верно?

1)  Все              углы      равнобедренного треугольника равны между собой.

2)  Диагонали ромба пересекаются под прямым углом.

3)  В            прямоугольном      треугольнике длина гипотенузы равна сумме длин катетов.

4.              Один из углов, образованных при пересечении двух прямых в 2 раза больше другого. Найдите меньший угол. Ответ дайте в градусах.

5. 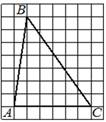   В треугольнике ABC угол C равен 159°. Найдите внешний угол при вершине C. Ответ дайте в градусах.

6.              На клетчатой бумаге размером клетки 1x1 изображен треугольник ABC. Найдите длину средней линии треугольника параллельной стороне AC.

7.              Две      прямые           пересечены     третьей. Один из накрест лежащих углов равен 67°, другой-55°.          На       сколько           градусов         нужно увеличить        меньший угол, чтобы   прямые стали параллельными?

8.              В прямоугольном треугольнике один из острых углов равен 48°. Найдите больший из углов, на которые высота, проведенная к гипотенузе, делит прямой угол.

9.              В треугольнике АВС провели среднюю линию КМ, параллельную стороне АВ. Периметр треугольника СКМ равен 17. Найдите периметр треугольника АВС

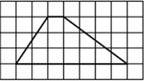
10.          На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите длину ее средней линии.

Вариант 2

1.       Какое из следующих утверждений верно?

1)        Сумма углов любого треугольника 180°.

2)   Если угол острый, то смежный с ним угол тоже острый.

3)   Любые две прямые имеют ровно одну общую точку.

2.         Какое из следующих утверждений верно?

1)   Вертикальные углы равны.

2)   Каждая из биссектрис равнобедренного треугольника являются высотой.

3)   Диагонали трапеции пересекаются и делятся точкой пересечения пополам.

3.         Какое из следующих утверждений верно?

1)  Если в ромбе один из углов равен 90°, то этот ромб является квадратом.

2)  В равностороннем треугольнике каждая биссектриса делит противоположную сторону пополам.

3)  Все углы ромба равны.

4.    Один из углов, образованных при пересечении двух прямых в 3 раза больше другого. Найдите меньший угол. Ответ дайте в градусах.

5.    В треугольнике ABC угол C равен 168°. Найдите внешний угол при вершине C. Ответ дайте в градусах.

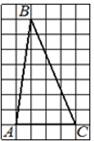
6.    На клетчатой бумаге размером клетки 1x1 изображен треугольник ABC. Найдите длину средней линии треугольника параллельной стороне AC.

7.    Две прямые           пересечены     третьей. Один из накрест лежащих углов равен 85°, другой-71°.  На       сколько           градусов         нужно увеличить        меньший угол, чтобы   прямые стали параллельными?

8.    В прямоугольном треугольнике один из острых углов равен 25°. Найдите больший из углов, на которые высота, проведенная к гипотенузе, делит прямой угол.

9.    В треугольнике АВС провели среднюю линию DМ, параллельную стороне АВ. Периметр треугольника СDМ равен 16. Найдите периметр треугольника АВС

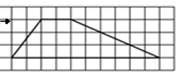
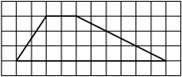
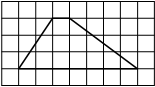
10. На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите длину ее средней линии.

Дополнительные задачи.

1.     Периметр равнобедренного треугольника в пять раз больше основания и на 9 см больше боковой стороны. Найдите боковую сторону треугольника.

2.     В треугольнике АВС угол А меньше угла В на 100°, а внешний угол при вершине А больше внешнего угла при вершине В в три раза. Найдите наибольшую разность двух внешних углов треугольника АВС.

Ответы.

Ответы на дополнительные задачи.

1.    6 см

2.    110°