2.15 Многоугольник. Сумма углов выпуклого мнеогоугольника

Многоугольник. Сумма углов выпуклого многоугольника.

Повторяем теорию

Произвольный многоугольник – объединение замкнутой ломаной и ее внутренней области.

Саму ломаную называют границей многоугольника, а ее внутреннюю область -

внутренней областью многоугольника.

Звенья границы многоугольника называются сторонами многоугольника, а вершины - вершинами многоугольника.

Отрезок, соединяющий две противолежащие вершины многоугольника, называют его диагональю.

Правильный многоугольник – это многоугольник, у которого все стороны равны и все углы равны.

Произвольный четырехугольник – это фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.

Соседние вершины — вершины четырехугольника, являющиеся концами одной из                                                      его                                                          сторон. Противолежащие вершины — не соседние вершины.

Соседние  стороны  —  стороны,  выходящие  из  одной  вершины.

Противолежащие стороны — не соседние стороны.

Диагональ четырехугольника — отрезок, соединяющий противолежащие вершины четырехугольника.

Периметр четырехугольника — сумма длин всех сторон.

Выпуклый четырёхугольник — четырехугольник, лежащий в одной полуплоскости относительно прямой, содержащей его сторону.

Внешний угол четырехугольника — угол, смежный с углом четырехугольника.

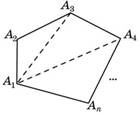Произвольный многоугольник Сумма     внутренних      углов                 n- угольника равна 180⁰∙(n-2)

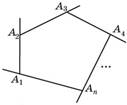Сумма внешних углов n-угольника равна 360⁰

Проверяем себя.

Т1. Вставьте пропущенное слово

а)   Простая   замкнутая  ломаная  называется                                         ,   если      ее соседние звенья не лежат на одной прямой.

б) Выпуклый многоугольник называется                                        , если у него все стороны и все углы равны.

в)             Сумма            длин             всех             сторон                четырехугольника называется                                                       четырехугольника.

г)    Отрезок,    соединяющий    противолежащие    вершины       четырехугольника, называется                                              .

д)      Стороны      четырехугольника,      исходящие      из      одной         вершины, называют                         сторонами.

Ответ: а) многоугольником; б) правильным; в) периметром; г) диагоналями; д) соседними

Т2. Выбери верное утверждение

а) Сумма углов выпуклого четырёхугольника равна:

а)180⁰; б) 360⁰; в)90⁰

Ответ: б)360

Т3. Выбери верное утверждение

В n-угольнике сумма внешних углов равна сумме внутренних углов. Этот многоугольник имеет сторон: а) 4; б) 6; в) 8.

Ответ: а)4

Решаем задачи

1.     Найдите сумму внутренних углов выпуклого: а) четырехугольника, б) шестиугольника, в) одиннадцатиугольника

Ответ: а)360, б)720, в)1620

2.     Сколько сторон имеет n-угольник, если сумма его внутренних углов равна: а)540⁰, б)1440⁰, в) 1080⁰

Ответ: а)5, б)10, в)8

3.     Найдите углы выпуклого четырехугольника, если их градусные меры пропорциональны числам: а) 2, 4 ,4, 8; б) 3, 6, 6, 9; в) 0,5; 1; 1; 2

Ответ: а) 40,80,80,160, б) 45,90,90,135, в) 40,80,80,160

4.          Найдите углы А, В, С выпуклого четырехугольника ABCD, если:

а) ∠A=∠B=∠C, а ∠D=60⁰ б) ∠A=∠B=∠C, а ∠D=135⁰ в) ∠A=∠B=∠C, а ∠D=30⁰

Ответ: а) 100, б) 75, в) 110.

5.     Три угла  четырехугольника             равны:   а)   45⁰,105⁰,120⁰;   б)30⁰,80⁰,140⁰;       в) 93⁰,160⁰,77⁰. Найдите его четвертый угол.

Ответ: а)90, б) 110 в)30

6.     Внутри         угла   А   взята   точка,   из   которой   опущены   на   его       стороны перпендикуляры. Найдите углы получившегося четырехугольника, если:

а) ∠A=75⁰; б) ∠A=54⁰; в) ∠A=103⁰

Ответ: а) 105, б) 126, в) 77

7.     Сумма углов n-угольника равна: а)360⁰; б)720⁰; в) 1440⁰. Найдите n. Ответ: а) 4, б) 6, в)10.

Самостоятельнаяработа

Вариант 1

1. Найдите сумму внутренних углов выпуклого двадцатиугольника.

2. Сколько        сторон   имеет   n-угольник,   если   сумма   его   внутренних      углов равна1800⁰?

3. Три угла четырехугольника равны: а) 40⁰, 110⁰, 120⁰. Найдите его четвертый угол.

Ответы: 1)3240, 2)12, 3)90.

Вариант 2

1. Найдите      углы   выпуклого   четырехугольника,   если    их   градусные   меры пропорциональны числам 4 ,8, 8, 16

2. Найдите углы А, В, С выпуклого четырехугольника ABCD, если: а) ∠A=∠B=∠C, а ∠D=27⁰.

3. Внутри угла А взята точка, из которой опущены на его стороны перпендикуляры. Найдите углы получившегося четырехугольника, если ∠A=175⁰. Ответы: 1)40,80,80,160, 2)111, 3)5.