2.15 Отрезки, связанные с окружностью.

Отрезки, связанные с окружностью.

Хорда, диаметр, радиус.

Повторяем теорию.

Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, - радиусом окружности.

У любой окружности бесконечно много радиусов и все они имеют одинаковую длину.

Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется ее диаметром. У любой окружности бесконечно много диаметров.

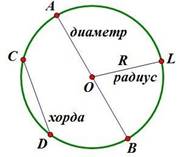
O – центр окружности

OA = OB = OL = R – радиусы окружности CD – хорда

AB – диаметр

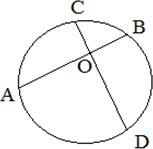Свойство пересекающихся хорд. Если две хорды пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

АO · OB = CO · OD

Проверяем себя.

Т1. Вставьте пропущенное слово:

а)   Отрезок,   соединяющий   центр   окружности   с   какой-либо   точкой окружности, называется                  окружности.

б) Хорда – отрезок, соединяющий                      окружности. в) Расстояния от центра окружности до равных хорд            .

г) Центр окружности является                          любого диаметра.

Ответ: а) радиусом; б) две точки; в) равны; г) серединой.

Т2. Выберете верное утверждение:

а) Все хорды окружности равны между собой.

б) Все диаметры окружности равны между собой.

в) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.

г) Равные хорды параллельны.

Ответ: б).

Т3. Выберете верное утверждение:

а)   Если   концы  хорды  соединить   с   центром  окружности,  получится равносторонний треугольник.

б) Параллельные хорды равны.

в) Диаметром называется отрезок, проходящий через центр окружности.

г) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.

Ответ: г

Решаем задачи.

1.     а) Точки А и К лежат на окружности с центром в точке О и радиусом 3 см. ∠АОК=60°. Найдите длину хорды АК.

Ответ: 3

б) Точки А и К лежат на окружности с центром в точке О и радиусом 5 см.

∠АОК=60°. Найдите длину хорды АК.

Ответ: 5

в) Точки А и К лежат на окружности с центром в точке О и радиусом 7 см.

∠АОК=60°. Найдите длину хорды АК.

Ответ: 7.

2.     а) Диаметр АВ окружности радиусом 6 см образует с хордой АК угол 45°. Найдите расстояние от точки К до прямой АВ.

Ответ: 6

б) Диаметр АВ окружности радиусом 16 см образует с хордой АК угол 45°.

Найдите расстояние от точки К до прямой АВ.

Ответ: 16

в) Диаметр АВ окружности радиусом 9 см образует с хордой АК угол 45°.

Найдите расстояние от точки К до прямой АВ.

Ответ: 9.

3.                а) Хорда АВ равна 18 см. ОА и ОВ – радиусы окружности, причем угол АОВ равен 90°. Найдите расстояние от точки О до хорды АВ.

Ответ: 9.

б) Хорда АВ равна 14 см. ОА и ОВ – радиусы окружности, причем угол АОВ равен 90°. Найдите расстояние от точки О до хорды АВ.

Ответ: 7.

в) Хорда АВ равна 13 см. ОА и ОВ – радиусы окружности, причем угол АОВ равен 90°. Найдите расстояние от точки О до хорды АВ.

Ответ: 6,5.

4.              а) Хорды АВ и СD окружности пересекаются в точке М. Найдите МА, если МВ=3 см, МС=4 см, МD=9 см.

Ответ: 12.

б) Хорды АВ и СD окружности пересекаются в точке М. Найдите МА, если МВ=8 см, МС=6 см, МD=4 см.

Ответ: 3.

в) Хорды АВ и СD окружности пересекаются в точке М. Найдите МА, если МВ=3 см, МС=6 см, МD=8 см.

Ответ: 16.

5.              а) Найдите расстояние от центра окружности, радиус которой равен 13 см, до её хорды, длина которой равна 10 см.

Ответ: 12.

б) Найдите расстояние от центра окружности, радиус которой равен 15 см, до её хорды, длина которой равна 18 см.

Ответ: 12.

в) Найдите расстояние от центра окружности, радиус которой равен 26 см, до её хорды, длина которой равна 48 см.

Ответ: 10.

6.               а) Расстояние от центра окружности, радиус которой равен 29 см, до её хорды равно 21 см. Найдите длину хорды.

Ответ:40.

б) Расстояние от центра окружности, радиус которой равен 20 см, до её хорды равно 16 см. Найдите длину хорды.

Ответ: 24.

в) Расстояние от центра окружности, радиус которой равен 26 см, до её хорды равно 10 см. Найдите длину хорды.

Ответ: 48.

7.                а) Отрезки АВ и СD являются хордами окружности. Найдите длину хорды СD, если АВ=16, а расстояния от центра окружности до хорд АВ и СD равны 15 и 8 соответственно.

Ответ: 30.

б) Отрезки АВ и СD являются хордами окружности. Найдите расстояние до центра окружности до хорды СD, если АВ=30, СD=40, а расстояние от центра окружности до хорды АВ равно 20.

Ответ:15

в) Отрезки АВ и СD являются хордами окружности. Найдите расстояние до центра окружности до хорды СD, если АВ=6, СD=8, а расстояние от центра окружности до хорды АВ равно 4.

Ответ: 3.

Задачи с развернутым ответом.

1.        Окружность радиуса 12 см касается внешним образом второй окружности в точке С. Прямая, проходящая через точку С, пересекает первую окружность в точке А, а вторую окружность – в точке В. Найдите радиус второй окружности, если АС=6 см, ВС=7 см.

Ответ: 14.

2.    Расстояние между центрами двух пересекающихся окружностей равно 44 см. Радиусы окружностей равны 17 см и 39 см. Найдите длину общей хорды окружностей.

Ответ:30.