2.16 Прямые, связанные с окружностью. Касательная, секущая.

Прямые, связанные с окружностью. Касательная, секущая.

Повторяем теорию

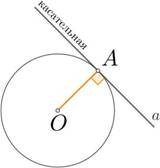
Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

A – точка касания

Свойство касательной: касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. A ⊥ a

Признак касательной: если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.

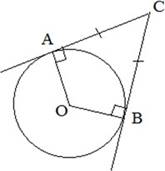
Отрезки AB и AC называются отрезками касательных, проведенных из точки A.

Свойство отрезков касательных.

Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

AC = CB, ∠ACO = ∠BCO.

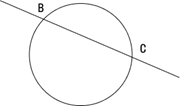Секущая                 к     окружности    –     это     прямая, пересекающая окружность в двух точках.

BC – секущая

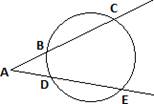Свойство: если через точку, лежащую вне окружности, проведены две секущие, то произведение одной секущей на ее внешнюю часть равно произведению другой секущей на ее внешнюю часть.

AС × AB = AE × AD

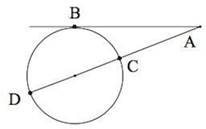Свойство секущей и касательной:

если через точку, лежащую вне окружности, проведены касательная и секущая, то квадрат отрезка касательной равен произведению секущей на ее внешнюю часть.

AB² = AС × AD

Проверяем себя.

Т1. Вставьте пропущенное слово:

а) Прямая, имеющая с окружностью только одну общую точку, называется

                              к окружности.

б) Касательная к окружности                                         к радиусу, проведенному в точку касания.

в) Отрезки касательных к окружности, проведенные из одной точки, и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

г) Если через точку, лежащую вне окружности, проведены две секущие, то произведение одной секущей на ее                              равно произведению другой секущей на ее                            .

Ответ: а) касательной; б) перпендикулярна; в) равны; г) внешнюю часть; внешнюю часть.

Т2. Выберите верное утверждение

а) Касательная к окружности параллельна радиусу, проведенному в точку касания.

б) Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.

в) Если через точку, лежащую вне окружности, проведены две секущие, то произведение отрезков одной секущей равно произведению отрезков другой секущей.

г) Радиус перпендикулярен касательной окружности

Ответ: б)

Т3. Выберите верное утверждение

а) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.

б) Если угол между радиусом и прямой, проведенной через его конец, лежащий на окружности, тупой, то прямая не пересекает окружность.

в) Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к радиусу, то она является секущей.

г) Касательной называется прямая, имеющая с окружностью общую точку.

Ответ: а)

Решаем задачи.

1.     а) Через точку А окружности с центром О проведена касательная АВ. Найдите радиус окружности, если ОВ=6 см, ∠АОВ=60°.

Ответ: 3

б) Через точку А окружности с центром О проведена касательная АВ. Найдите радиус окружности, если ОВ=16 см, ∠АОВ=60°.

Ответ: 8

в) Через точку А окружности с центром О проведена касательная АВ. Найдите радиус окружности, если ОВ=14 см, ∠АОВ=60°.

Ответ: 7.

2.     а) Отрезки касательных АВ и ВС, проведенных из точки В к окружности с центром в точке О, образуют угол, равный 60°, ОВ=28 см. Найдите длину отрезка АО.

Ответ: 14

б) Отрезки касательных АВ и ВС, проведенных из точки В к окружности с центром в точке О, образуют угол, равный 60°, ОВ=20 см. Найдите длину отрезка АО.

Ответ: 10

в) Отрезки касательных АВ и ВС, проведенных из точки В к окружности с центром в точке О, образуют угол, равный 60°, ОВ=18 см. Найдите длину отрезка АО.

Ответ: 9.

3.                    а) Прямая СВ касается окружности с центром в точке А и радиусом 4 см в точке В. Найдите расстояние АС, если ВС=3 см.

Ответ: 5

б) Прямая СВ касается окружности с центром в точке А и радиусом 5 см в точке В. Найдите расстояние АС, если ВС=12 см.

Ответ: 13

в) Прямая СВ касается окружности с центром в точке А и радиусом 6 см в точке В. Найдите расстояние АС, если ВС=8 см.

Ответ: 10.

4.                     а) Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=4, AC=64. Найдите AK.

Ответ: 16

б) Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=6, AC=54. Найдите AK.

Ответ: 18

в) Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=2, AC=8. Найдите AK.

Ответ: 4.

5.                    а) Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=2, ВC=6. Найдите AK.

Ответ: 4.

б) Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=2, ВC=16. Найдите AK.

Ответ: 6.

в) Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=4, ВC=12. Найдите AK.

Ответ: 8.

6.                     а) Через точку A, лежащую вне окружности с центром в точке О, проведены две касательные АМ и АК. АМ=10, ∠МАО=30°. Найдите расстояние между точками М и К.

Ответ: 10.

б) Через точку A, лежащую вне окружности с центром в точке О, проведены две касательные АМ и АК. АМ=22, ∠МАО=30°. Найдите расстояние между точками М и К.

Ответ: 22.

в) Через точку A, лежащую вне окружности с центром в точке О, проведены две касательные АМ и АК. АМ=17, ∠МАО=30°. Найдите расстояние между точками М и К.

Ответ: 17.

7.                    а) Прямая АВ – касательная к окружности с центром в точке О. АВ=2 см, ∠АОВ=45°. Найдите радиус ОА.

Ответ: 2.

б) Прямая АВ – касательная к окружности с центром в точке О. АВ=15 см,

∠АОВ=45°. Найдите радиус ОА.

Ответ: 15.

в) Прямая АВ – касательная к окружности с центром в точке О. АВ=23 см,

∠АОВ=45°. Найдите радиус ОА.

Ответ: 23.

Задачи с развернутым ответом.

1.      Из одной точки проведены к окружности касательная и секущая. Секущая равна 10 см, а её внутренний отрезок больше внешнего на длину касательной. Найдите длину касательной.

Ответ: 5 см.

2.  Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В. Найдите АС, если диаметр окружности равен 15, а АВ=4.

Ответ: 16.