2.17 Вписанная в треугольник окружность.

Вписанная в треугольник окружность.

Повторяем теорию.

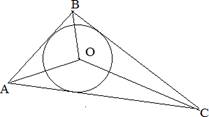Если все стороны треугольника касаются окружности, то окружность называется вписанной в треугольник, а треугольник называется описанным около этой окружности.

В любой треугольник можно вписать окружность и только одну.

Центр вписанной окружности в треугольник – это точка пересечения биссектрис треугольника.

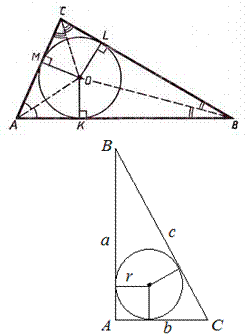O – центр окружности,

AO, BO, CO – биссектрисы улов

Площадь треугольника равна произведению его полупериметра на радиус вписанной в него окружности 𝑺 = 𝒑 · 𝒓.

Если треугольник прямоугольный, то

𝒓 = 𝒂+𝒃−𝒄 .

𝟐

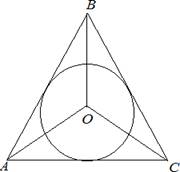
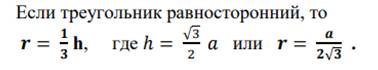
Проверяем себя.

Т1. Вставьте пропущенное слово:

а)    Если    все    стороны   треугольника                      

окружность называется вписанной в треугольник.

окружности,   то

б) Площадь треугольника равна произведению его                        на радиус вписанной в него окружности.

в) Центр вписанной окружности в треугольник – это точка пересечения

                       треугольника.

Ответ: а) касаются; б) полупериметра; в) биссектрис.

Т2. Выберите верное утверждение

а)   Центр  вписанной  в   треугольник  окружности  совпадает  с   точкой пересечения его биссектрис.

б) Центр вписанной в равнобедренный треугольник окружности совпадает с точкой пересечения его медиан.

в)   Центр  вписанной   в   треугольник  окружности  совпадает  с   точкой пересечения его высот.

г)   Центр   вписанной  в   треугольник  окружности  совпадает  с   точкой пересечения его серединных перпендикуляров.

Ответ: а)

Т3. Выберите верное утверждение

1)  Окружность называется вписанной в треугольник, если все вершины треугольника лежат на окружности.

2)  Если точка М равноудалена от вершин треугольника АВС, то она является центром вписанной окружности.

3)  Окружность называется вписанной в треугольник, если все стороны треугольника касаются окружности.

Ответ: 3.

Решаем задачи.

1.     а) В треугольнике АВС стороны АС=8, ВС=15, угол С равен 90°. Найдите радиус окружности, вписанной в этот треугольник.

Ответ: 3

б) В треугольнике АВС стороны АС=10, ВС=24, угол С равен 90°. Найдите радиус окружности, вписанной в этот треугольник.

Ответ: 4

в) В треугольнике АВС стороны АС=5, ВС=12, угол С равен 90°. Найдите радиус окружности, вписанной в этот треугольник.

Ответ: 2

2.     а) Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.

Ответ: 6.

б) Периметр треугольника равен 76, а радиус вписанной окружности равен

8. Найдите площадь этого треугольника.

Ответ: 304.

в) Периметр треугольника равен 88, а радиус вписанной окружности равен

10. Найдите площадь этого треугольника.

Ответ: 440.

3.      а) Площадь треугольника равна 24, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника

Ответ: 24

б) Площадь треугольника равна 60, а радиус вписанной окружности равен

4. Найдите периметр этого треугольника

Ответ: 30

в) Площадь треугольника равна 102, а радиус вписанной окружности равен

6.   Найдите периметр этого треугольника

Ответ: 34.

4.     а)                 Сторона        правильного  треугольника  равна √3 Найдите  радиус окружности, вписанной в этот треугольник.

Ответ: 0,5

б)   Сторона   правильного   треугольника   равна 6√3.   Найдите   радиус окружности, вписанной в этот треугольник.

Ответ: 3

в)    Сторона    правильного   треугольника    равна 8√3 Найдите    радиус окружности, вписанной в этот треугольник.

Ответ: 4.

5.     а)                  Найдите         радиус   окружности,   вписанной   в   равносторонний треугольник, если высота треугольника равна 6.

Ответ: 2

б) Найдите радиус окружности, вписанной в равносторонний треугольник, если высота треугольника равна 36.

Ответ: 12

в) Найдите радиус окружности, вписанной в равносторонний треугольник, если высота треугольника равна 18.

Ответ: 6

6.     а) Окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС в точках М, Ки Р соответственно. Найдите периметр треугольника АВС, если АР=4 см, ВМ=6 см, СК=3 см.

Ответ: 26.

б) Окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС в точках М, Ки Р соответственно. Найдите периметр треугольника АВС, если АМ=5 см, ВК=2 см, СР=4 см.

Ответ: 22

в) Окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС в точках М, Ки Р соответственно. Найдите периметр треугольника АВС, если АМ=4 см, ВК=6 см, СР=4 см.

Ответ: 28.

7.     а) Найдите радиус окружности, вписанной в треугольник, если один из углов треугольника равен 90°, а расстояние от центра окружности до вершины этого угла равно 4√2 см.

Ответ: 4.

б) Найдите радиус окружности, вписанной в треугольник, если один из углов треугольника равен 120°, а расстояние от центра окружности до вершины этого угла равно 18√3 см

Ответ: 27.

в) Найдите радиус окружности, вписанной в треугольник, если один из углов треугольника равен 90°, а расстояние от центра окружности до вершины этого угла равно 8√2 см.

Ответ: 8.

Задачи с развернутым ответом.

1.         Расстояние от точки пересечения биссектрис равнобедренного треугольника до его основания равно 3 см, а до вершины, противолежащей этому основанию, 5 см. Найдите основание треугольника.

Ответ: 12

2.       В равнобедренный треугольник АВС с основанием АС вписана окружность. Она касается стороны ВС в точке D. Найдите радиус этой окружности, если ВD=2 и СD=3.

Ответ: 1,5