
Описанная около треугольника окружность.
Повторяем теорию.
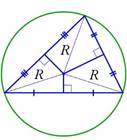 Если все вершины треугольника лежат на окружности, то окружность называется описанной около треугольник,
а треугольник называется вписанным в эту окружность.
Если все вершины треугольника лежат на окружности, то окружность называется описанной около треугольник,
а треугольник называется вписанным в эту окружность.
Около любого треугольника можно описать окружность и только одну.
Центр описанной окружности в треугольник – это точка пересечения серединных перпендикуляров к сторонам треугольника.
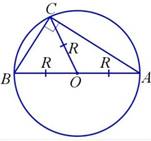 Если треугольник
прямоугольный, то центр описанной окружности – это середина гипотенузы.
Если треугольник
прямоугольный, то центр описанной окружности – это середина гипотенузы.
Радиус описанной окружности равен половине гипотенузы или длине медианы, проведенной из вершины прямого угла к гипотенузе.
![]() OB = OC = OA=𝑹 = 𝟏
OB = OC = OA=𝑹 = 𝟏
𝟐
АВ .
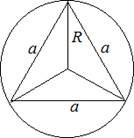 Если треугольник равносторонний, то
Если треугольник равносторонний, то
![]() , где h=
, где h=![]() или R=
или R=![]()
![]()
![]()
![]() R=2r
R=2r
Если треугольник произвольный, то
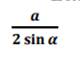
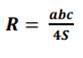
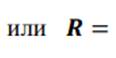
Если треугольник тупоугольный, то центр описанной окружности находится вне треугольника.
С каждым треугольником связаны четыре точки: точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпедикуляров к сторонам и точка пересечения высот (или их продолжений). Эти четыре точки называют замечательными точками треугольника.
Проверяем себя.
Т1. Вставьте пропущенное слово:
а) Если серединные перпендикуляры к сторонам треугольника пересекаются на стороне этого треугольника, то он является
.
б) Центр описанной около треугольника окружности – это точка пересечения к сторонам треугольника.
в) Если треугольник прямоугольный, то центр описанной окружности – это
гипотенузы.
г) Если треугольник тупоугольный, то центр описанной окружности находится треугольника.
Ответ: а) прямоугольным; б) серединных перпендикуляров; в) середина; г)
вне.
Т2. Выберите верное утверждение:
а) Центр описанной около треугольника окружности всегда лежит внутри
этого треугольника
б) Если точка М равноудалена от вершин треугольника АВС, то она является центром описанной окружности.
в) Высоты треугольника совпадают с серединными перпендикулярами.
г) Точка пересечения средних линий треугольника является замечательной точкой треугольника.
Ответ: б).
Т3. Выберите верное утверждение:
1) Точка пересечения высот треугольника (или их продолжений) не относится к его замечательным точкам.
2) Окружность называется описанной около треугольника, когда окружность пересекает все стороны этого треугольника.
3) Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
4) Радиус окружности, описанной около прямоугольного треугольника, равен гипотенузе этого треугольника.
Ответ: 3.
Решаем задачи.
1. а) В треугольнике АВС стороны АС=8, ВС=15, угол С равен 90°. Найдите радиус описанной около этого треугольника окружности.
Ответ: 8,5
б) В треугольнике АВС стороны АС=10, ВС=24, угол С равен 90°. Найдите радиус описанной около этого треугольника окружности.
Ответ: 13
в) В треугольнике АВС стороны АС=12, ВС=5, угол С равен 90°. Найдите радиус описанной около этого треугольника окружности.
Ответ: 6,5.
2. а) Найдите диаметр окружности, описанной около треугольника, если
![]() синус одного из углов треугольника равен 3
синус одного из углов треугольника равен 3
7
, а противолежащая этому углу
сторона равна 15 см.
Ответ: 35
б) Найдите диаметр окружности, описанной около треугольника, если
![]() синус одного из углов треугольника равен 4 ,
а противолежащая этому углу
синус одного из углов треугольника равен 4 ,
а противолежащая этому углу
9
сторона равна 16 см.
Ответ: 36
в) Найдите диаметр окружности, описанной около треугольника, если
![]() синус одного из углов треугольника равен 5 ,
а противолежащая этому углу
синус одного из углов треугольника равен 5 ,
а противолежащая этому углу
6
сторона равна 20 см.
Ответ: 24.
3.
![]() а)
Найдите диаметр окружности, описанной около прямоугольного треугольника, если косинус
одного из углов
треугольника равен 3 , а
а)
Найдите диаметр окружности, описанной около прямоугольного треугольника, если косинус
одного из углов
треугольника равен 3 , а
7
прилежащий к этому углу катет равен 18 см.
Ответ: 42
б) Найдите диаметр окружности, описанной около прямоугольного треугольника, если косинус одного из углов треугольника равен 0,25, а прилежащий к этому углу катет равен 1 см.
Ответ: 4
в) Найдите диаметр окружности, описанной около прямоугольного
![]() треугольника, если косинус одного
из углов треугольника равен 4 , а
треугольника, если косинус одного
из углов треугольника равен 4 , а
9
прилежащий к этому углу катет равен 12 см.
Ответ: 27.
4. а) Найдите радиус окружности, описанной около треугольника, если одна из сторон треугольника равна 20 см, а расстояние от центра окружности до этой стороны равно 24 см.
Ответ: 26
б) Найдите радиус окружности, описанной около треугольника, если одна из сторон треугольника равна 24 см, а расстояние от центра окружности до этой стороны равно 5 см.
Ответ: 13
в) Найдите радиус окружности, описанной около треугольника, если одна из сторон треугольника равна 48 см, а расстояние от центра окружности до этой стороны равно 10 см.
Ответ: 26.
5. а) Найдите радиус окружности, описанной около равностороннего треугольника, если радиус окружности, вписанной в этот треугольник, равен 42 см.
Ответ: 84
б) Найдите радиус окружности, описанной около равностороннего треугольника, если радиус окружности, вписанной в этот треугольник, равен 21 см.
Ответ: 42
в) Найдите радиус окружности, описанной около равностороннего треугольника, если радиус окружности, вписанной в этот треугольник, равен 26 см.
Ответ: 52.
6. а) Центр окружности, описанной около треугольника АВС, лежит на стороне АВ. Радиус окружности равен 17 см. Найдите АС, если ВС=16 см.
Ответ:30
б) Центр окружности, описанной около треугольника АВС, лежит на стороне АВ. Радиус окружности равен 25 см. Найдите АС, если ВС=48 см.
Ответ: 14
в) Центр окружности, описанной около треугольника АВС, лежит на стороне АВ. Радиус окружности равен 12,5 см. Найдите АС, если ВС=7 см.
Ответ: 24.
7. а) В равнобедренном треугольнике АВС ∠А=30°, ∠С=30°. Сторона АВ равна 4 см. Найдите радиус окружности, описанной около треугольника АВС.
Ответ: 4
б) В равнобедренном треугольнике АВС ∠А=30°, ∠С=30°. Сторона АВ равна 14 см. Найдите радиус окружности, описанной около треугольника АВС.
Ответ: 14
в) В равнобедренном треугольнике АВС ∠А=30°, ∠С=30°. Сторона АВ равна 8 см. Найдите радиус окружности, описанной около треугольника АВС.
Ответ: 8.
Задачи с развернутым ответом.
1. В равнобедренном треугольнике боковая сторона равна 10 см. а биссектриса, проведенная к основанию, - 8 см. Найдите радиус окружности, описанной около этого треугольника.
Ответ: 6,25
2. В треугольнике АВС биссектриса угла А делит высоту, проведенную из вершины В, в отношении 5:4, считая от точки В. Найдите радиус окружности, описанной около треугольника АВС, если ВС=18.
Ответ: 15
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.