2.18 Прямоугольник. Квадрат

Прямоугольник, квадрат Повторяем теорию.

Прямоугольником называется параллелограмм, у которого все углы прямые.

Основные свойства прямоугольника.

1. 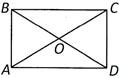     В прямоугольнике противоположные стороны равны.

AB=CD, BC=AD

2.     Диагонали    прямоугольника    точкой пересечения делятся пополам.

AO=CO, BO=DO

3.      Диагонали прямоугольника равны.

AC=BD

Признак прямоугольника. Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

Квадратом называется прямоугольник, у которого все стороны равны.

Квадрат является прямоугольником, поэтому является параллелограммом, у которого все стороны равны, т.е. ромбом.

Основные свойства квадрата:

1.      Все углы квадрата прямые.

2.     Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

Проверяем себя:

Т1. Продолжите предложение:

а) Если диагонали параллелограмма равны, то это                      . б) Диагонали                                           равны и взаимно перпендикулярны. в) В прямоугольнике противоположные стороны                  .

Ответы: а) прямоугольник; в) квадрата; г) равны.

Т2. Выберите верные утверждения:

а) Диагонали любого прямоугольника делят его на 4 равных треугольника. б) Диагонали прямоугольника точкой пересечения делятся пополам.

в) Если в ромбе один из углов равен 90°, то такой ромб – квадрат. г) В любом прямоугольнике диагонали взаимно перпендикулярны. д) Любой квадрат является прямоугольником.

Ответ: б), в), д).

Т3. Выберите неверное утверждение:

а) Диагонали прямоугольника делят углы прямоугольника пополам. б) В прямоугольнике сумма углов равна 360°.

в) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм – квадрат.

г) Периметр квадрата равен сумме длин всех его сторон.

д)      Существует     прямоугольник,      диагонали     которого         взаимно перпендикулярны.

Ответ: а)

Решаем задачи

1. 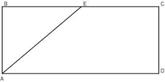    а) Биссектриса угла А прямоугольника ABCD пересекает сторону BC в точке E. Найдите периметр прямоугольника, если BE=4, CE=19.

Ответ: 54

б)    Биссектриса    угла    А    прямоугольника    ABCD

пересекает сторону BC в точке E. Найдите периметр прямоугольника, если

BE=8, CE=13.

Ответ: 58

в) Биссектриса угла А прямоугольника ABCD пересекает сторону BC в точке E. Найдите периметр прямоугольника, если BE=5, CE=14.

Ответ: 48

2.     а) Периметр квадрата равен 160. Найдите площадь этого квадрата.

Ответ: 1600

б) Периметр квадрата равен 32. Найдите площадь этого квадрата.

Ответ: 64

в) Периметр квадрата равен 68. Найдите площадь этого квадрата.

Ответ: 289

3.     а) Диагональ прямоугольника образует угол 50° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Ответ: 80

б) Диагональ прямоугольника образует угол 44° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах. Ответ: 88

в) Диагональ прямоугольника образует угол 86° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах. Ответ: 8

4. 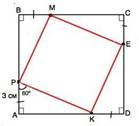    а) На сторонах AB, BC, CD, AD квадрата ABCD отмечены соответственно точки P, M, E и K так, что AP=BM=CE=DK=3 см, ∠АРК=60°.

Найдите периметр четырехугольника PMEK.

Ответ: 24

б) На сторонах    AB, BC, CD, AD квадрата ABCD отмечены соответственно точки P, M, E и K так, что AP=BM=CE=DK= 5

см, угол АРК равен 60°. Найдите периметр четырехугольника PMEK.

Ответ: 40

в) На сторонах AB, BC, CD, AD квадрата ABCD отмечены соответственно точки P, M, E и K так, что AP=BM=CE=DK= 6 см, угол АРК равен 60°. Найдите периметр четырехугольника PMEK.

Ответ: 48

5. 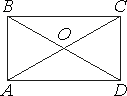                   а)    Диагонали    AC    и    BD    прямоугольника    ABCD

пересекаются в точке О, ВО=7, АВ= 6. Найдите АС.

Ответ: 14

б) Диагонали AC и BD прямоугольника ABCD пересекаются в точке О, ВО=8, АВ= 9. Найдите АС.

Ответ: 16

в) Диагонали AC и BD прямоугольника ABCD пересекаются в точке О, ВО=13, АВ= 5. Найдите АС.

Ответ: 26

6.     а) Найдите площадь прямоугольника, если его периметр равен 44 и одна его сторона на 2 больше другой.

Ответ: 120

б) Найдите площадь прямоугольника, если его периметр равен 58 и одна его сторона на 5 больше другой.

Ответ: 204

в) Найдите площадь прямоугольника, если его периметр равен 26 и одна его сторона на 3 больше другой.

Ответ: 40

7. 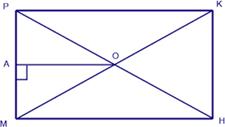    а)          В   прямоугольнике MPKH  диагонали пересекаются в точке О. Отрезок ОA является высотой      треугольника   MОP,   ∠AОP   =             15°. Найдите ∠ОHK. Ответ укажите в градусах. Ответ: 75

б) В прямоугольнике MPKH диагонали пересекаются в точке О. Отрезок ОA является высотой треугольника MОP, ∠AОP = 50°. Найдите ∠ОHK. Ответ укажите в градусах.

Ответ: 40

в) В прямоугольнике MPKH диагонали пересекаются в точке О. Отрезок ОA является высотой треугольника MОP, ∠AОP = 28°. Найдите ∠ОHK. Ответ укажите в градусах.

Ответ: 62.

Задачи с развернутым ответом

1.     В прямоугольнике диагональ делит угол в отношении 2:1, меньшая его сторона равна 5 см. Найдите диагональ заданного прямоугольника. Ответ: 10

2.     Внутри квадрата ABCD выбрана точка М так, что треугольник AMD

равносторонний. Найдите величину угла AMB. Ответ: 75

3.     Диагональ AC квадрата ABCD равна 18,4 дм. Прямая, проходящая через точку А и перпендикулярная к прямой АС, пересекает прямые ВС и CD соответственно в точках M и N. Найдите MN.

Ответ: 36,8 дм.