2.19 Трапеция, средняя линия трапеции

Трапеция, средняя линия трапеции

Повторяем теорию

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

Параллельные стороны трапеции называются ее основаниями, две другие стороны – боковыми сторонами.

Основные определения и свойства трапеции

Проверяем себя.

Т1. Выберите верное утверждение:

а) Диагонали трапеции перпендикулярны и точкой пересечения делятся пополам.

б) Сумма внутренних углов трапеции равна 360°. в) Каждая трапеция является параллелограммом.

г) Если две стороны выпуклого четырехугольника параллельны, то этот четырехугольник – трапеция.

Ответ: б)

Т2. Выберите неверные утверждения:

а) У любой трапеции основания параллельны.

б) Диагональ трапеции делит ее на два равных треугольника.

в) Отрезок, соединяющий середины диагоналей трапеции, равен полуразности ее оснований.

г) Диагонали трапеции пересекаются и точкой пересечения делятся пополам.

Ответ: б), г)

Т3. Сформулируйте свойство трапеции:

Биссектрисы углов при боковой стороне трапеции                     . а) параллельны,

б) равны,

в) перпендикулярны, г) образуют угол 120°. Ответ: в)

Решаем задачи.

1.     а) Найдите высоту BН трапеции ABCD, если углы ABC и BCD равны соответственно 135° и 150°, а CD=26.

Ответ: 13

б) Найдите высоту BН трапеции ABCD, если углы ABC и BCD равны соответственно 135° и 150°, а CD=18.

Ответ: 9

в)     Найдите    высоту BН трапеции ABCD,    если     углы ABC и BCD        равны соответственно 135° и 150°, а CD=40.

Ответ: 20

2.     а) Биссектрисы углов A и B при боковой стороне AB трапеции ABCD

пересекаются в точке F. Найдите AB, если AF=24, BF=10.

Ответ: 26

б)  Биссектрисы  углов  A  и  B  при  боковой  стороне  AB  трапеции  ABCD

пересекаются в точке F. Найдите AB, если AF=15, BF=8. Ответ: 17

в)  Биссектрисы  углов  A  и  B  при  боковой  стороне  AB  трапеции  ABCD

пересекаются в точке F. Найдите AB, если AF=16, BF=12. Ответ: 20

3. 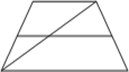    а) Основания трапеции равны 14 и 19. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Ответ: 9,5

б) Основания трапеции равны 1 и 17. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Ответ: 8,5

в) Основания трапеции равны 3 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Ответ: 5,5

4. 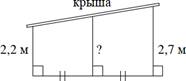    а) Наклонная крыша установлена на трех вертикальных опорах, основания которых расположены на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 2,2 м, высота большой опоры 2,7 м. Найдите высоту средней опоры. Ответ дайте в метрах.

Ответ: 2,45

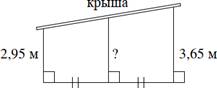б) Наклонная крыша установлена на трех вертикальных опорах, основания которых расположены на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 2,95 м, высота большой опоры 3,65 м. Найдите высоту средней опоры. Ответ дайте в метрах.

Ответ: 3,3

в) Наклонная крыша установлена на трех вертикальных опорах, основания которых расположены на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 2,25 м, высота большой опоры 2,85 м. Найдите высоту средней опоры. Ответ дайте в метрах.

Ответ: 2,55

5.     а) В трапеции ABCD ∠А=37°, ∠С=126°. Чему равна сумма градусных мер углов B и D? Ответ дайте в градусах.

Ответ: 197

б) В трапеции ABCD ∠В=128°, ∠С=115°. Чему равна сумма градусных мер углов А и D? Ответ дайте в градусах.

Ответ: 117

в) В трапеции ABCD ∠А=49°, ∠С=131°. Чему равна сумма градусных мер углов

B и D? Ответ дайте в градусах.

Ответ: 180

6.     а) В трапеции углы при большем основании равны 60°, а ее основания равны 6 и 10. Найдите периметр трапеции.

Ответ: 24

б) В трапеции высоты образуют с боковыми сторонами углы 30°, а ее основания равны 11 и 5. Найдите периметр трапеции.

Ответ: 28

в) В трапеции углы при большем основании равны 60°, а ее основания равны 21 и 15. Найдите периметр трапеции.

Ответ: 48

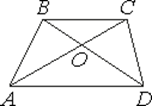
7.     а) Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=7, AC=20. Найдите AO.

Ответ: 14

б) Диагонали AC и BD трапеции ABCD с основаниями BC

и AD пересекаются в точке O, BC=3, AD=5, AC=24. Найдите AO.

Ответ: 15

в) Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=4, AD=9, AC=26. Найдите AO.

Ответ: 18

Задачи с развернутым ответом.

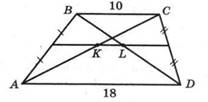
1.    Основания BC и AD трапеции ABCD равны 10 и

18      соответственно.      Найдите      отрезок          KL, соединяющий середины ее диагоналей.

Ответ: 4

2.    В трапеции ABCD AD и BC - основания, AD ˃ BC. На стороне AD отмечена точка K так, что KBCD – параллелограмм. Периметр треугольника ABK равен 25 , DK= 6. Найдите периметр трапеции.

Ответ: 37

3.    Каждое основание AD и BC трапеции ABCD продолжено в обе стороны. Биссектрисы внешних углов A и B этой трапеции пересекаются в точке P, биссектрисы внешних углов C и D пересекаются в точке R. Найдите периметр трапеции ABCD, если длина отрезка PR равна 24 см.

Ответ: 48 см.