2.19 Вписанная в четырехугольник, правильный многоугольник окружность.

Вписанная в четырехугольник, правильный многоугольник окружность.

Повторяем теорию.

Окружность называется вписанной в четырехугольник, если она касается всех его сторон. Четырехугольник тогда называется описанным.

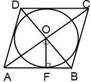
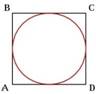
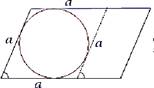
Не во всякий четырехугольник можно вписать окружность. Окружность можно вписать в ромб, квадрат.

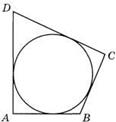В      любом     описанном     четырехугольнике     суммы противоположных сторон равны.

AB + DC = AD + BC

Обратное    утверждение:    Если    суммы    противоположных    сторон выпуклого четырехугольника равны, то в него можно вписать окружность.

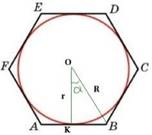В любой правильный многоугольник можно вписать окружность и притом только одну.

Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах.

AK = KB

Центр   окружности,   описанной   около   правильного   многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.

Эта точка называется центром правильного многоугольника.

Проверяем себя.

Т1. Вставьте пропущенное слово:

а) Сторона квадрата больше радиуса вписанной в него окружности в

            раза.

б) В любом описанном четырехугольнике суммы противоположных сторон

                      .

в) Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их                           .

г) В любой                          многоугольник можно вписать окружность и притом только одну.

Ответ: а) два; б) равны; в) серединах; г) правильный.

Т2. Выберите верное утверждение

а) Радиус окружности, вписанной в правильный шестиугольник, относится к его стороне как √3:2.

б) В любой прямоугольник можно вписать окружность.

в) В любую трапецию можно вписать окружность.

г) В любой многоугольник можно вписать окружность.

Ответ: а).

Т3. Выберите верное утверждение

а) Диаметр вписанной в квадрат окружности совпадает с диагональю квадрата.

б) Площадь четырехугольника равна произведению его периметра на радиус вписанной окружности.

в) Сторона квадрата равна удвоенному диаметру вписанной окружности. г) В ромб можно вписать окружность.

Ответ: г)

Решаем задачи.

1.     а) В квадрат вписана окружность. Найдите радиус окружности, если диагональ квадрата равна 12√2.

Ответ: 6

б) В квадрат вписана окружность. Найдите радиус окружности, если диагональ квадрата равна 3√2.

Ответ: 1,5

в) В квадрат вписана окружность. Найдите радиус окружности, если диагональ квадрата равна 8√2.

Ответ: 4

2.     а) Найдите площадь квадрата, описанного около окружности радиуса

40.

Ответ: 6400.

б) Найдите площадь квадрата, описанного около окружности радиуса 7.

Ответ: 196

в) Найдите площадь квадрата, описанного около окружности радиуса 15.

Ответ: 900.

3.                     а) Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен √3.

Ответ: 2

б)   Найдите   сторону  правильного  шестиугольника,  описанного  около окружности, радиус которой равен 17√3.

Ответ: 34

в)   Найдите  сторону  правильного  шестиугольника,  описанного  около окружности, радиус которой равен 10√3.

Ответ: 20

4.                     а) Около окружности описана трапеция, периметр которой равен 40. Найдите её среднюю линию.

Ответ: 10

б) Около окружности описана трапеция, периметр которой равен 60.

Найдите её среднюю линию.

Ответ: 15

в) Около окружности описана трапеция, периметр которой равен 30.

Найдите её среднюю линию.

Ответ: 7,5.

5.                    а) Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.

Ответ:4

б) Боковые стороны трапеции, описанной около окружности, равны 6 и 8.

Найдите среднюю линию трапеции.

Ответ: 7

в) Боковые стороны трапеции, описанной около окружности, равны 12 и

15.   Найдите среднюю линию трапеции.

Ответ: 13,5.

6.     а) Найдите площадь прямоугольной трапеции, боковые стороны которой равны 12 см и 18 см, если известно, что в эту трапецию можно вписать окружность.

Ответ: 180

б) Найдите площадь прямоугольной трапеции, боковые стороны которой равны 10 см и 16 см, если известно, что в эту трапецию можно вписать окружность.

Ответ: 130

в) Найдите площадь прямоугольной трапеции, боковые стороны которой равны 14 см и 20 см, если известно, что в эту трапецию можно вписать окружность.

Ответ: 238.

7.     а) В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 5.

Ответ: 20

б)     В     параллелограмм    вписана    окружность.    Найдите    периметр параллелограмма, если одна из его сторон равна 12.

Ответ: 48

в)     В     параллелограмм    вписана    окружность.    Найдите    периметр параллелограмма, если одна из его сторон равна 9.

Ответ: 36.

Задачи с развернутым ответом.

1.

2√2 дм?

Ответ: в 1,3.

2.     В ромб вписана окружность. Точка касания делит сторону ромба на отрезки, равные 9 см и 4 см. Найдите диаметр окружности.

Ответ: 12.