22. Дидактический материал_1. Вариант 2

Приложение 1

Практическая работа:

Правила техники безопасности: “Правила пользования циркулем и ножницами”.

Циркуль – это чертежный инструмент. Циркуль от латинского слова “circulus” - круг, окружность (“circa” - вокруг, кругом, то есть цирк – это круг). Сейчас уже нельзя сказать, кто именно изобрел этот инструмент - история не сохранила для нас его имя, но легенды Древней Греции приписывают авторство Талосу, племяннику знаменитого Дедала, первого «воздухоплавателя» древности. История циркуля насчитывает уже несколько тысяч лет - судя по сохранившимся начерченным кругам, инструмент был знаком еще вавилонянам и ассирийцам (II - I века до нашей эры). На территории Франции, в галльском кургане был найден железный циркуль (I век нашей эры), во время раскопок в Помпеях было найдено много древнеримских бронзовых циркулей.

С ним нужно работать осторожно. Нельзя подносить иглой к лицу и нельзя передавать циркуль соседу “иглой вперед”. Ножницами также нужно пользоваться осторожно: к лицу не подносить, передавать соседу “тупым концом”, т. е. колечками.

Ножки циркуля двигаются. Что надо сделать, чтобы начертить большую окружность – развести их или сдвинуть ближе? (Если сдвинуть ближе ножки циркуля, то получишь маленькую окружность, чтобы начертить большую окружность, ножки циркуля нужно развести).

Задание 1.

Обозначь в своей тетради буквы О и А. Острый конец циркуля поставь в точку О, а карандаш циркуля поставь в точку А. Относительно точки О проведи кривую с помощью циркуля. Какая фигура получилась? На этой кривой обозначь буквы В и С. Проведи отрезки ОВ и ОС. Сравни длины отрезков ОА, ОВ и ОС. Подумай: как расположены точки А, В, С относительно точки О?

Определение 1: Множество всех точек, расположенных на одинаковом расстоянии от заданной точки (центра),  называется окружностью.

Определение 2: Часть плоскости, ограниченная окружностью называется кругом.

Точка О – центр окружности.

Отрезок, соединяющий центр и точку на окружности (CD), является радиусом этой окружности. Радиус обозначается буквой R.

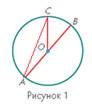Отрезок, проходящий через центр и соединяющий две любые точки окружности (AB), называется диаметром. Диаметр обозначается буквой D (d). (Рисунок 1).

т .О — центр круга;

ОА, ОВ, ОС— радиусы окружности: ОА = OB =R; (Радиус по-латыни radius – это спица колеса).

АС- хорда (это отрезок, соединяющий любые две точки на окружности);

АВ - диаметр: АВ = D. (Диаметр – это наибольшая из хорд окружности, проходящая через центр окружности. С греческого диаметр – это «поперечник»).

Задание 2.

Определи соотношение между диаметром и радиусом окружности.

На рисунке определим длины отрезков АО и BO. На АB лежит т. О, причем AO = BO = OC и равны R, следовательно, О - середина АB, поэтому АО =BO= АB : 2

Вывод: R=D:2,откуда D = 2R.

Задание 3.

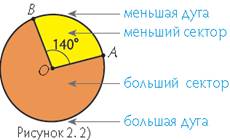
 Определи соотношение между дугой и круговым сектором.

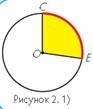
На рисунке 2.1 даны элементы окружности (круга).

Часть окружности между точками С и Е называется дугой. Она обозначается знаком ∪CE. Часть круга, ограниченная радиусами ОС и ОЕ, называется круговым сектором.

Рассмотри рисунок и сделай вывод. (Чем больше дуга, тем больше сектор и наоборот).

Задание 4 (дополнительное).

Построй отрезок MN длиной 5 см. Построй окружности с центром М, радиусом 4 см и с центром N, радиусом 3,5 см. Одну из точек пересечения окружностей обозначь буквой D. Найди расстояния от точки D до точек M и N. (Ответ: DM = 4 см, DN = 3,5 см.

Вызов. Сколько радиусов и сколько диаметров можно провести? Сколько хорд? Сколько дуг получится? Построй несколько радиусов, диаметров.

Сделай выводы.