22. Длина окружности. Сфера. Методические. Вариант 2

Методические указания к уроку

тема "Длина окружности. Площадь круга. Шар. Сфера"

Цели обучения

6.3.3.2 знать, что отношение длины окружности к ее диаметру есть число постоянное;

6.3.3.3 знать и применять формулу длины окружности;

6.3.3.4 знать и применять формулу площади круга;

6.3.1.7 иметь представление о шаре и сфере.

Организационный момент. Мотивация к учебной деятельности. Беседа.

Понятие круга знакома учащимся еще с начальной школы. Урок следует начать с напоминания, что математика — это не только наука о числах и действиях с ними (кстати, этот раздел называется арифметикой); математика изучает еще геометрические фигуры и их свойства (этот раздел математики называется геометрией). Что среди геометрических фигур есть круг, окружность, определить их отличие практически на примерах.

-Как часто нам приходится встречаться с кругом, окружностью в повседневной жизни? Где мы можем увидеть круг?

(Форму круга могут иметь тарелка, блюдце, барабан…)

А форму окружности? (Гимнастический обруч, ювелирное кольцо...)

В чем различие?

Например:

Пицца, пирог, блин, тарелка и т.д. - круг; Гимнастический обруч, ювелирное кольцо и т.д  - окружность.

Каким инструментом пользуются и как, чтобы начертить окружность?

Если нет инструмента, то как начертить окружность на местности? (Можно с помощью веревки. Если один конец закрепить в центре, а с другим концом обойти вокруг, то получится окружность. Если нет верёвки, то ее можно заменить палкой. Если нет ни верёвки, ни палки, то можно двоим взяться за руки, один из них будет стоять на месте, а другой обойдет вокруг него, то получится окружность).

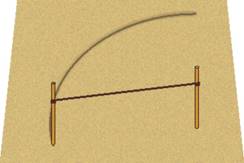
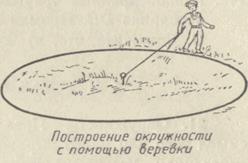
Предложить ученикам определить тему и цели урока.

Работа в парах. 1) Практическая работа. Создать пары из представителей разных уровней обучаемости.

Цель практической работы:

·         Напомнить определения круга, окружности и их элементов. Вспомнить практические навыки, полученные в начальной школе, пользования циркулем для вычерчивания окружности.

·          Провести инструктаж по технике безопасности о правилах пользования циркулем и ножницами

·          Провести практическую работу по построению окружностей и их элементов.

Создание проблемной ситуации в форме задания.

Приложение 1

Практическая работа:

Правила техники безопасности: “Правила пользования циркулем и ножницами”.

Циркуль – это чертежный инструмент. Циркуль от латинского слова “circulus” - круг, окружность (“circa” - вокруг, кругом, то есть цирк – это круг). Сейчас уже нельзя сказать, кто именно изобрел этот инструмент - история не сохранила для нас его имя, но легенды Древней Греции приписывают авторство Талосу, племяннику знаменитого Дедала, первого «воздухоплавателя» древности. История циркуля насчитывает уже несколько тысяч лет - судя по сохранившимся начерченным кругам, инструмент был знаком еще вавилонянам и ассирийцам (II - I века до нашей эры). На территории Франции, в галльском кургане был найден железный циркуль (I век нашей эры), во время раскопок в Помпеях было найдено много древнеримских бронзовых циркулей.

С ним нужно работать осторожно. Нельзя подносить иглой к лицу и нельзя передавать циркуль соседу “иглой вперед”. Ножницами также нужно пользоваться осторожно: к лицу не подносить, передавать соседу “тупым концом”, т. е. колечками.

Ножки циркуля двигаются. Что надо сделать, чтобы начертить большую окружность – развести их или сдвинуть ближе? (Если сдвинуть ближе ножки циркуля, то получишь маленькую окружность, чтобы начертить большую окружность, ножки циркуля нужно развести).

Задание 1.

Обозначь в своей тетради буквы О и А. Острый конец циркуля поставь в точку О, а карандаш циркуля поставь в точку А. Относительно точки О проведи кривую с помощью циркуля. Какая фигура получилась? На этой кривой обозначь буквы В и С. Проведи отрезки ОВ и ОС. Сравни длины отрезков ОА, ОВ и ОС. Подумай: как расположены точки А, В, С относительно точки О?

Определение 1: Множество всех точек, расположенных на одинаковом расстоянии от заданной точки (центра),  называется окружностью.

Определение 2: Часть плоскости, ограниченная окружностью называется кругом.

Точка О – центр окружности.

Определение 3: Отрезок, соединяющий центр и точку на окружности (CD), является радиусом этой окружности. Радиус обозначается буквой R.

Определение 4: 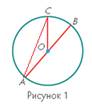Отрезок, проходящий через центр и соединяющий две любые точки окружности (AB), называется диаметром. Диаметр обозначается буквой D (d). (Рисунок 1).

т .О — центр круга;

ОА, ОВ, ОС— радиусы окружности: ОА = OB =R; (Радиус по-латыни radius – это спица колеса).

АС- хорда (это отрезок, соединяющий любые две точки на окружности);

АВ - диаметр: АВ = D. (Диаметр – это наибольшая из хорд окружности, проходящая через центр окружности. С греческого диаметр – это «поперечник»).

Задание 2.

Определи соотношение между диаметром и радиусом окружности.

На рисунке определим длины отрезков АО и BO. На АB лежит т. О, причем AO = BO = OC и равны R, следовательно, О - середина АB, поэтому АО =BO= АB : 2

Вывод: R=D:2,откуда D = 2R.

Задание 3.

 Определи соотношение между дугой и круговым сектором.

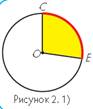
На рисунке 2.1 даны элементы окружности (круга).

Определение 4: Часть окружности между точками С и Е называется дугой. Она обозначается знаком ∪CE. Определение 5: Часть круга, ограниченная радиусами ОС и ОЕ, называется круговым сектором.

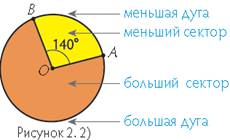Рассмотри рисунок и сделай вывод. (Чем больше дуга, тем больше сектор и наоборот).

Задание 4 (дополнительное).

Построй отрезок MN длиной 5 см. Построй окружности с центром М, радиусом 4 см и с центром N, радиусом 3,5 см. Одну из точек пересечения окружностей обозначь буквой D. Найди расстояния от точки D до точек M и N. (Ответ: DM = 4 см, DN = 3,5 см.

Вызов. Сколько радиусов и сколько диаметров можно провести? (Множество) Сколько хорд? (Множество) Сколько дуг получится? (Множество) Построй несколько радиусов, диаметров.

Сделай выводы.

Вызов. Каждая линия имеет длину. Как же найти длину окружности? Можно ли ее измерить (вычислить)? Всегда ли отношения длины окружности к длине диаметра равны?

Соотношение между диаметром и длиной окружности учащиеся определяют опытным путем и делают вывод.

Ход исследования. Учащиеся проводят эксперименты с ранее заготовленными крышками от банок (можно монетами) разных радиусов. Работая в паре: один может обводить на листе бумаги крышку карандашом, получит круг и вырезать, а другой взять нитку и обвести ею крышку (монету), выпрямить нитку и измерить ее длину. Затем измеряют диаметр круга, находят отношение длины круга к его диаметру.

Учитель:

·          отмечает этапы математического исследования;

·          контролирует деятельность учащихся; наблюдает за точностью выполнения инструкций исследовательского листа, техники безопасности;

·          подводит учащихся к выводу.

Учащиеся:

·          знакомятся с планом исследования и выполняют, согласно этому плану, задания;

·          поэтапно выполняют математическое исследование;

·          обобщают результаты исследования;

·          делают выводы.

Учитель обращает внимание на обозначения: длины окружности, диаметра.

2) Исследовательская работа по определению числа .

Приложение 2

Вычисление частного длины окружности и ее диаметра.

Оборудование: Крышки банок:

Нитки:,

Линейка:, циркуль, карандаш, бумага, ножницы.

Задание №1

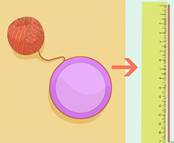Крышка банки – идеальный круг.

Измерьте длину окружности С настолько точно, насколько это возможно.

Для этого: 1) Обверните нитку вокруг крышки как можно плотнее.

2) Отметьте точку совпадения начала и конца.

3) Измерьте длину нитки с помощью линейки, запишите С=...

Задание № 2: Измерьте диаметр окружности.

Диаметр D (d)– длина отрезка, проходящего через центр окружности и любые две точки, лежащие на окружности. Как измерить точно диаметр?

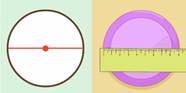 Для этого: 1) На бумаге обвести крышку, используя карандаш с очень тонким грифелем.

2) Вырезать полученный круг и сложить пополам.

3) Измерить полученный отрезок.  d=...

Задание №3

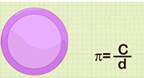
Посчитайте частное длины окружности, и ее диаметра (с вашими значениями) на калькуляторе. Запишите результат.

Обозначьте частное: .

Задание №4

Чтобы уточнить расчеты, повторите ваши действия (1-3) с несколькими различными крышками (окружностями), а затем сверьте результаты. Чему равно среднее арифметическое результатов?

Сделайте вывод: Чему равно частное длины окружности и ее диаметра?

Вывод. Длина окружности примерно в 3 раза больше его диаметра, следовательно, C = 3d или C = 2∙3∙R.

Индивидуальная работа. Работа с учебником. Решение практических задач.

После окончания исследовательской работы предложить учащимся ознакомиться с материалом учебника, содержащим определения числа . (Пи) (Можно добавить интересную информацию о том, что обозначение буквой  не случайное, потому что это первая буква в греческом слове περιφερια («периферия») — круг). Значение числа: π ≈ 3,14159265359 ≈ 3,14

3,14159265359 ≈ 3,1416 - легко запомнить применяя следующую аналогию:

«ЧТО Я ЗНАЮ О КРУГАХ»: ЧТО - 3, Я -1, ЗНАЮ - 4, О -1, КРУГАХ - 6 букв.

Учащиеся должны усвоить, что какой бы ни была окружность, отношение ее длины к диаметру является постоянным числом. Это число принято обозначать буквой  (читается-"пи"). Введя обозначения длины окружности буквой С, а ее диаметр буквой d записать формулу:  или .

Введя обозначения площади круга буквой S записать формулу: , где  - радиус

Для закрепления и оценки уровня умения применять изученные формулы, предложить ученикам решить практические задачи. Ученики выполняют задания индивидуально, но имеют возможность обсудить непонятные вопросы с товарищем по парте или обратиться к однокласснику, которому он доверяет. Учитель помогает наиболее нуждающимся.

Индивидуальная работа в группе. Решение задач.

Объединить учащихся в однородные группы по 4-6 учеников, согласно выбранному уровню. Задание у всех групп одинаковое, но совместная работа с одноклассниками одного уровня позволит раскрыться каждому ученику

Для закрепления, предложить ученикам решить задачи из Приложения 3, где группам предложить решить первые три задачи, если группа закончит раньше, то решает следующие задачи.

Ученики работают индивидуально, но имеют возможность спросить непонятные вопросы и сверить свои решения с одноклассниками по группе.

1.      Длина окружности равна 12,56 см. Найдите площадь круга, радиус которого в 3 раза больше радиуса данной окружности (число  округлите до сотых).

А) 11,304 см²

В) 113,04 см²

С) 18,84 см²

D) 123,24 см²

E) 1130,4 см²

2.      Длина окружности равна 31,4 см. Найдите площадь круга, радиус которого на 1 см больше радиуса данной окружности (число  округлите до сотых).

А) 11,304 см²

В) 1130,4 см²

С) 113,04 см²

D) 123,24 см²

E) 18,84 см²

3.      За сколько времени можно облететь на самолете Землю вдоль экватора на высоте 10 км, двигаясь со скоростью 1200 км/ч? Результат округлите до 0,1 час. ( Радиус экватора приближенно равен 6370 км).

Ответ: 33,4 ч.

4.      Длина круга увеличилась с 157 см до 226,08 см. На сколько увеличился радиус круга?

Ответ: 11 см

5.      Радиус круга увеличили с 10 см до 11 см. На сколько увеличилась длина окружности?

Ответ: 2 см.

Ключ

Теоретические упражнения. Рассмотреть рисунок к теме устно в парах, написать предложения самостоятельно. Проверить сверяя с презентацией.

Приложение 4

Допиши предложения, используя рисунок:

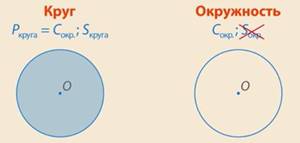Когда мы говорим про круг, то речь идет о двух объектах: ...

Круг – это плоская фигура, у него есть ....

Окружность – это линия, граница круга. У нее нет ..., но есть .... 

Радиус, диаметр, хорда, дуга - это элементы ...

Для обобщения изученного материала, можно при наличии времени просмотреть видео.

Беседа. Рефлексия.

 Повторить в чем отличие окружности и круга, применение формул длины окружности и площади круга.

Учитель организует рефлексию в форме методики незаконченных предложений. Учащиеся высказываются одним предложением, выбирая начало фразы на доске:

Сегодня я узнал… Я научился… Меня удивило…У меня получилось… Было трудно…

Домашнее задание. Сообщение о числе .

Знать определения окружности, круга, формулы и решить задания из уровня А и В №...,№....

На уроке предусмотрена дифференциация в виде работы в однородных группах (одного уровня обучаемости). Ученики самостоятельно выбирают уровень сложности заданий. Предусмотрена самопроверка по ключу, в ходе которой ученики оценивают умение применять формулы. В ходе коллективной деятельности при решении задач устно оценивается умение применять теорию и ранее изученный материал при решении нового типа задач.   Соблюдение правил техники безопасности при видах деятельности на уроке: при пользовании циркулем и ножницами. Следить за осанкой учащихся.

Скачано с www.znanio.ru