2.22 Проверочная работа "Многоугольники"

Практическая работа по теме: «Многоугольники».

Оборудование:     ножницы,     бумага,     проволока,     бумажные                             заготовки многоугольников

Повторяем теорию.

Основные свойства параллелограмма:

В   параллелограмме   противоположные   углы  и   противоположные     стороны равны. AB = CD, BC = AD; ∠A = ∠C, ∠B = ∠D

Диагонали параллелограмма точкой пересечения делятся пополам. AO = OC, BO = OD

Биссектриса    угла   параллелограмма    отсекает    от    него                        равнобедренный треугольник

Биссектрисы     соседних     углов     параллелограмма     перпендикулярны,     а биссектрисы противоположных углов параллельны или лежат на одной прямой В параллелограмме сумма углов, прилежащих к одной стороне, равна 180^o.∠А +

∠В = 180^o,   ∠А + ∠D = 180^o

Основные свойства ромба

В ромбе противоположные углы и противоположные стороны равны. AB = CD, BC = AD; ∠A = ∠C, ∠B = ∠D

Диагонали ромба точкой пересечения делятся пополам. AO = OC, BO = OD Диагонали ромба взаимно перпендикулярны и делят его углы пополам.

Высоты ромба равны.

Основные свойства прямоугольника

В прямоугольнике противоположные углы и стороны равны.

Диагонали прямоугольника равны и точкой пересечения делятся пополам.

Основные свойства квадрата.

Все углы квадрата прямые.

Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

Проверяем себя.

Т1. Вставьте пропущенное слово

а) Четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны называется                                 .

б)    Четырехугольник,    у    которого    противоположные    стороны       попарно параллельны называется                                                      .

в) Сумма длин всех сторон четырехугольника называется                               . г) Две несмежные стороны четырехугольника называются                                . д) Отрезок, соединяющий любые две не соседние вершины многоугольника, называется                                         многоугольника.

Ответы:     а)     трапецией;     б)     параллелограммом;     в)                     периметром; г) противоположными; д) диагональю.

Т2. Выбери верные утверждения

а) В параллелограмме противоположные стороны равны.

б)   Диагонали   прямоугольника   равны,   взаимно  перпендикулярны,      точкой пересечения делятся пополам и делят углы прямоугольника пополам.

в) В трапеции противоположные углы равны.

г) В равнобедренной трапеции углы при каждом основании равны. д) Все стороны ромба равны.

е) Диагонали ромба точкой пересечения делятся пополам.

Ответы: а); г); д); е).

Т3. Выбери верное утверждение

Диагонали какого четырехугольника имеют такие свойства:

Диагонали равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы четырехугольника пополам.

а) прямоугольник; б) произвольный четырехугольник; в) квадрат; г) ромб; д) трапеция; е) параллелограмм

Ответ: в).

Решаем задачи.

1.     а) К отрезку в его концах восстановите по одну сторону от него два равных перпендикуляра и их концы соедините отрезком. Является ли полученный четырехугольник прямоугольником? Перечислите его свойства.

Ответ: да.

Основные свойства прямоугольника:

В прямоугольнике противоположные углы и стороны равны

Диагонали прямоугольника равны и точкой пересечения делятся пополам

б) Постройте два неравных взаимно перпендикулярных отрезка, делящихся в точке пересечения пополам. Концы отрезков последовательно соедините. Является ли полученный четырехугольник ромбом? Перечислите его свойства.

Ответ: да. свойства ромба

В ромбе противоположные углы и противоположные стороны равны. AB = CD, BC = AD; ∠A = ∠C, ∠B = ∠D

Диагонали ромба точкой пересечения делятся пополам. AO = OC, BO = OD

Все стороны ромба равны.

Диагонали ромба взаимно перпендикулярны и делят его углы пополам. Диагонали ромба лежат на биссектрисах его углов.

Высоты ромба равны

в) Постройте два равных и параллельных отрезка. Соедините их концы непересекающимися отрезками. Верно ли, что получившийся четырехугольник является параллелограммом? Перечислите его свойства.

Ответ: да. Основные свойства параллелограмма:

В параллелограмме противоположные углы и противоположные стороны равны. AB = CD, BC = AD; ∠A = ∠C, ∠B = ∠D

Диагонали параллелограмма точкой пересечения делятся пополам. AO = OC, BO = OD

Биссектриса    угла    параллелограмма    отсекает    от    него                         равнобедренный треугольник

Биссектрисы соседних углов параллелограмма перпендикулярны, а биссектрисы противоположных углов параллельны или лежат на одной прямой

В параллелограмме сумма углов, прилежащих к одной стороне, равна 180^o.

∠А + ∠В = 180^o, ∠А + ∠D = 180^o

2.     а) Вырезать из листа бумаги равнобокую трапецию. Что необходимо сделать, чтобы получить из нее параллелограмм?

3. 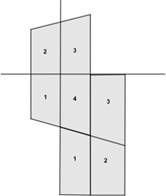    а) Паркетчик, вырезая квадраты из дерева, проверял их так: он сравнивал длины сторон, и если все четыре стороны были равны, то считал квадрат вырезанным правильно. Надежна ли такая проверка?

Ответ: Такая проверка недостаточна. Четырехугольник мог выдержать такое испытание, не будучи квадратом, ромб тоже имеет равные стороны

Другой паркетчик проверял свою работу иначе: он мерил не стороны, а диагонали. Если обе диагонали оказывались равными, паркетчик считал квадрат вырезанным правильно. Вы тоже так думаете?

Ответ: Эта проверка ненадежна. В квадрате, конечно, диагонали равны, но не всякий четырехугольник с равными диагоналями есть квадрат. Равные диагонали могут быть у прямоугольника и у равнобокой трапеции

Третий паркетчик при проверке квадратов убеждался в том, что все 4 части, на которые диагонали разделяют друг друга, равны между собой. По его мнению, это доказывало, что вырезанный четырехугольник есть квадрат.

Ответ: Этим свойством обладают не только диагонали квадрата, но и диагонали прямоугольника

б) Швее нужно отрезать кусок полотна в форме квадрата. Отрезав несколько кусков, она проверяет свою работу тем, что перегибает четырехугольный кусок по диагонали и смотрит, совпадают ли края. Если совпадают, значит, решает она, отрезанный кусок имеет в точности квадратную форму. Так ли это?

Ответ: Проверка далеко недостаточна. Есть четырехугольники, края которых при перегибании по диагонали совпадут, но все-таки это не квадраты. Это может быть ромб или четырехугольник произвольного вида.

Другая белошвейка не довольствовалась проверкой, применяемой ее подругой. Она перегибала отрезанный четырехугольник сначала по одной диагонали, затем, расправив полотно, перегибала по другой. И, только если края фигуры совпадали в обоих случаях, она считала квадрат вырезанным правильно. Что скажете вы о такой проверке?

Ответ: Эта проверка недостаточна. Это может быть не только квадрат, но и ромб. Чтобы действительно убедиться, квадратной ли формы отрезанный кусок, нужно, кроме того, что сделала швея, проверить также, равны ли диагонали или же углы.

в) Школьная мастерская изготовила партию пластин четырехугольной формы. Как проверить, будет ли пластина иметь форму прямоугольника, располагая лишь линейкой с делениями?

Ответ: 1) Измерим пары противоположных сторон четырёхугольника. Если они равны, то пластина имеет форму параллелограмма.

2) Измерим диагонали данной пластины, если они равны, то параллелограмм является прямоугольником

4.     а) В прямоугольной пластине нужно просверлить отверстие на равном расстоянии от ее вершин. Как найти центр этого отверстия?

Ответ: точка пересечения диагоналей

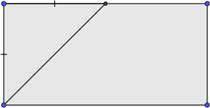б) Заготовлены одинаковые по ширине рейки в форме прямоугольников. Как не используя угломера, обрезать концы реек под углом 45 градусов, чтобы из них можно сделать раму?

Ответ: биссектриса угла отсекает равнобедренный треугольник

в) Имеется квадратный пруд. По его углам близ воды растут 4 старых дуба. Пруд понадобилось расширить. Как увеличить его размеры, не пересаживая деревья и сохранив форму квадрата?

Ответ: провести диагонали квадрата и параллельно диагоналям через вершины провести параллельные стороны нового квадрата.

5.     а) Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4:3, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.

Ответ: 28

б) Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4:3, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 66.

Ответ: 21

в) Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4:3, считая от вершины острого угла. Найдите меньшую сторону параллелограмма, если его периметр равен 110.

Ответ: 20

6.     а) Из медной проволоки, длиной 30 см, изготовить прямоугольник, стороны которого относятся как 2: 3.

Ответ: смежные стороны равны 6 см и 9 см

б) Из медной проволоки, длиной 20 см, изготовить прямоугольник, стороны которого относятся как 2: 3.

Ответ: смежные стороны равны 4 см и 6 см

в) Из медной проволоки, длиной 40 см, изготовить прямоугольник, стороны которого относятся как 2: 3.

Ответ: смежные стороны равны 8 см и 12 см

7.           

Задачи с развернутым ответом.

1.     Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите все углы ромба.

Ответ:60 ,60, 120, 120

2.     В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм — прямоугольник.