
Значения синуса, косинуса, тангенса для углов 30°, 45°,
60°.
Повторяем теорию
![]()
![]()
![]()
![]() Таблица значений sinα, cosα, tgα для углов
α, равных 30°, 45°, 60°.
Таблица значений sinα, cosα, tgα для углов
α, равных 30°, 45°, 60°.
|
α |
30° |
45° |
60° |
|
sin α |
1
2 |
2
2 |
3 2 |
|
cos α |
3
2 |
2
2 |
1
2 |
|
tg α |
1 = 3 3 3 |
1 |
3 |
![]()
![]()
![]()
![]()
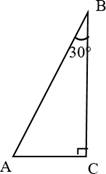 Катет прямоугольного треугольника, лежащий против
угла в 30°, равен
половине гипотенузы.
Катет прямоугольного треугольника, лежащий против
угла в 30°, равен
половине гипотенузы.
Если ∠ В = 30°, то АС =
1 AB.
![]() 2
2
Верно и обратное. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
Полезные факты.
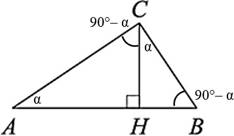 Сумма острых углов прямоугольного треугольника равна 90°: ∠A+∠B=90°.
Сумма острых углов прямоугольного треугольника равна 90°: ∠A+∠B=90°.
Следовательно, если в прямоугольном треугольнике один из острых углов равен 45°, то такой треугольник является равнобедренным.
Если в прямоугольном треугольнике ABC
провести высоту CH из прямого угла, то ∠BAC=∠BCH и ∠ABC=∠ACH.
Проверяем себя.
Т1. Вставьте пропущенное слово:
а) Косинусом острого угла прямоугольного треугольника называется отношение катета к гипотенузе.
б) Гипотенуза в больше катета, лежащего против угла
30°.
в) Значения синуса и косинуса угла в равны.
г) Если один из острых углов прямоугольного треугольника равен 45°, то треугольник
Ответ: а) прилежащего; б) два раза; в) 45°; г) равнобедренный.
Т2. Выберите верное утверждение.
а) Тангенс острого угла прямоугольного треугольника всегда меньше 1. б) sin 45° = 1.
в) sin 60°= cos 30°.
Ответ: в).
Т3. Выберите неверное утверждение.
а) Если два угла треугольника равны, то равны и значения тангенсов этих углов.
б) Если треугольник прямоугольный, то каждый его острый угол равен 45°.
в) sin 2 a + cos2 a = 1.
Ответ: б).
Решаем задачи.
1.
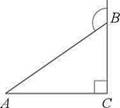 а)
В треугольнике АВС угол С равен 90°, АВ = 12. Внешний
угол при вершине В равен 120°.
Найдите ВС.
а)
В треугольнике АВС угол С равен 90°, АВ = 12. Внешний
угол при вершине В равен 120°.
Найдите ВС.
Ответ: 6.
б) В треугольнике АВС угол С равен 90°, АВ = 34.
Внешний угол при вершине В равен 120°. Найдите ВС.
Ответ: 17.
в) В треугольнике АВС угол С равен 90°, АВ = 40. Внешний угол при вершине В равен 120°. Найдите ВС.
Ответ: 20.
2. 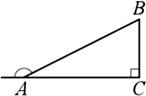 а) В прямоугольном треугольнике АВС внешний угол при вершине А равен 150°. Катет ВС
=19. Найдите гипотенузу АВ.
а) В прямоугольном треугольнике АВС внешний угол при вершине А равен 150°. Катет ВС
=19. Найдите гипотенузу АВ.
Ответ: 38.
б) В прямоугольном треугольнике АВС внешний
угол при вершине А равен 150°. Катет ВС = 41. Найдите гипотенузу АВ.
Ответ: 82.
в) В прямоугольном треугольнике АВС внешний угол при вершине А равен 150°. Катет ВС = 23. Найдите гипотенузу АВ.
Ответ: 46.
3.
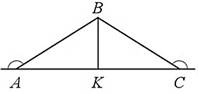 а) В ∆АВС внешние углы при вершинах А и С равны 150°, АВ
= 54. Найдите биссектрису ВК.
а) В ∆АВС внешние углы при вершинах А и С равны 150°, АВ
= 54. Найдите биссектрису ВК.
Ответ: 27.
б) В ∆АВС внешние углы при вершинах А и С равны 150°, АВ = 48. Найдите биссектрису ВК.
Ответ: 24.
в) В ∆АВС внешние углы при вершинах А и С равны 150°, АВ = 44. Найдите биссектрису ВК.
Ответ: 22.
4.
 а) Основания равнобедренной трапеции равны 15 и 9, один из углов равен 45°.
Найдите высоту трапеции.
а) Основания равнобедренной трапеции равны 15 и 9, один из углов равен 45°.
Найдите высоту трапеции.
Ответ: 3.
б) Основания равнобедренной трапеции равны 51 и 23, один из углов равен 45°. Найдите высоту трапеции.
Ответ: 14.
в) Основания равнобедренной трапеции равны 45 и 27, один из углов равен 45°. Найдите высоту трапеции.
Ответ: 9.
5.
 а) В равнобедренной трапеции основания
равны 12 и 27, острый угол равен 60°. Найдите ее периметр.
а) В равнобедренной трапеции основания
равны 12 и 27, острый угол равен 60°. Найдите ее периметр.
Ответ: 69.
б) В равнобедренной трапеции основания равны 29 и 50, острый угол равен 60°. Найдите ее периметр.
Ответ: 121.
в) В равнобедренной трапеции основания равны 45 и 74, острый угол равен 60°. Найдите ее периметр.
Ответ: 177.
6.
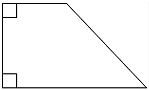 а) В прямоугольной
трапеции основания равны 3 и 5, а
один из углов равен 135°. Найдите меньшую боковую сторону.
а) В прямоугольной
трапеции основания равны 3 и 5, а
один из углов равен 135°. Найдите меньшую боковую сторону.
Ответ:2.
б) В прямоугольной трапеции основания равны 12 и 19, а один из углов равен 135°. Найдите меньшую боковую сторону.
Ответ: 7.
в) В прямоугольной трапеции основания равны 21 и 30, а один из углов равен 135°. Найдите меньшую боковую сторону.
Ответ: 9.
7.
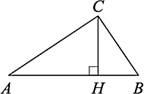 а) В треугольнике ABC угол C равен 90°, CH – высота, угол A равен 30°. Найдите AH, если AB =2.
а) В треугольнике ABC угол C равен 90°, CH – высота, угол A равен 30°. Найдите AH, если AB =2.
Ответ:1,5.
б) В треугольнике ABC угол C равен 90°, CH – высота, угол A равен 30°. Найдите ВH, если AB =4.
Ответ: 1.
в) В треугольнике ABC угол C равен 90°, CH – высота, угол A равен 30°. Найдите ВH, если AB =16.
Ответ: 4.
Задачи с развернутым ответом.
1. Найдите боковую сторону АВ трапеции ABCD, если углы ABC и BCD равны соответственно 60°и 135°, а CD=36.
![]() Ответ: 12 .
Ответ: 12 .
2.
![]() Найдите боковую
сторону AB трапеции ABCD, если углы ABC и BCD
равны соответственно 30° и 135°, а
CD=29.
Найдите боковую
сторону AB трапеции ABCD, если углы ABC и BCD
равны соответственно 30° и 135°, а
CD=29.
Ответ:
29 .
3. Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 150°, а CD=33.
![]() Ответ: 11 .
Ответ: 11 .
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.