23. Длина окружности. Методические. Вариант 2

Методические указания к уроку

тема "Длина окружности. Площадь круга. Шар. Сфера"

Цели обучения

6.3.3.2 знать, что отношение длины окружности к ее диаметру есть число постоянное;

6.3.3.3 знать и применять формулу длины окружности;

6.3.3.4 знать и применять формулу площади круга;

6.3.1.7 иметь представление о шаре и сфере.

Организационный момент. Мотивация к учебной деятельности.

Предложить вычислить значения дробей до сотых:

;  ;  ;  ; ;  ; ;  ; ;  ; ;  ; ;  ;

и сравнить с числом .

-             Значение какой из дробей более близко к числу Пи?

-             Когда лучше использовать число Пи в виде дроби?

-             Как называется место в цирке, где выступают артисты? (-Арена.)

-             А какую форму имеет арена? (-Арена имеет форму круга.)

-             Не только в цирке арена имеет форму круга, но и в некоторых видах спорта спортсмены выступают на площадках круглой формы. Как называются эти виды спорта? (вольная борьба, сумо, греко-римская борьба, самбо)

Предложить ученикам определить тему и цели урока – повторения.

Устные упражнения. Для понимания и умения различать круг и окружность, знать определения их элементов, решите с учащимися устно следующие 4 задания. Работа по готовым чертежам закрепит в памяти теоретический материал.

Задание №1

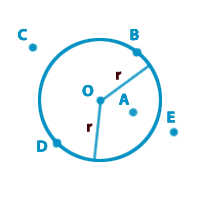1) Выберите верные утверждения, исходя из рисунка:

а) Точки C, B и E не принадлежат кругу.

 б) Точки D, B и O принадлежат окружности.

в) Точки A, B и O принадлежат кругу.

2) Выберите верные утверждения, исходя из рисунка:

а) Точка О является центром и окружности, и круга.

б) Точка О является центром окружности, но не центром круга.

в) Точки D и B не принадлежат окружности.

3) Выберите верные утверждения, исходя из рисунка:

а) Точки B и D не принадлежат кругу.

б) Точки A, B, D и O принадлежат кругу.

в) Точки B, D и E принадлежат кругу.

4) Выберите верные утверждения, исходя из рисунка:

а) Точки B и D разделяют окружность на 4 дуги.

б) Точки B и D разделяют окружность на 3 дуги.

в) Точки  B и D разделяют окружность на 2 дуги.

Задание №2

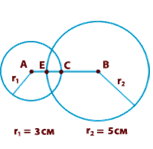 На рисунке построено две окружности, первая с центром в точке А радиусом r₁= 3 см и вторая с центром в точке B радиусом  r₂= 5 см.

Они пересекли отрезок AB в точках E и C. Найдите длины отрезков  ЕС, AE и BC,

если AB = 7 см.

Задание № 4

Чему равна длина красной части окружности, если ее радиус равен 33 дм?

Решение: C=2 πR. Длина красной части равна l=2/3∙C;  l= 138.16 дм=14 м.

Ответ: 14 м.

Письменные  упражнения. Чтобы правильно применять формулу длины окружности и площади круга учащиеся выполнять тест. Приложение 1.

1.      Выберите длину окружности с радиусом 5,5 см:

1) 17,27см;                 2) 34,54 см;                3) 69,08 см.

2.      Выберите длину окружности с радиусом 3 см:

1) 6,28 см;                  2) 9,42 см;                  3) 18,84 см

3.      Выберите радиус окружности, длина которой 6,28см:

1) 3 см;                       2)2 см;                        3)1 см.

4.      Выберите площадь круга с радиусом 3 см:

1) 28,26 см²;               2) 28,76 см²;              3) 56,52 см².

5.      Выберите радиус круга, площадь которого 12,56см²:

1) 2см;                        2) 3см;                        3) 4см.

Ключ

Повторение теоретического материала.

Историческая справка «Знакомство с историей числа π» (сообщение ученика).

В сообщении желательно чтобы следующая информация из Приложения 2 содержалась обязательно.

Предварительно учитель должен проверить сообщение ученика и одобрить, проверив достоверность информации. Прослушав информацию, учащиеся могут дополнить сообщение.

Из истории.

Число π – обозначение отношения длины окружности С к ее диаметру d.

Многие ученые – математики пытались доказать, что это отношение есть число постоянное, не зависящее от размеров окружности. Впервые это удалось сделать древнегреческому математику Архимеду. Он нашел довольно точное значение этого отношения. Архимед жил на Сицилии с 287 г. до 212 г. до н.э. Используя рассуждения, он доказал, что π ≈ 3, 14. В трактате «Измерение круга» Архимед предлагает метод определения числа π , который использовался до конца 17 в., и указывает две удивительно точные границы числа  π: .

На самом деле число π не может быть выражено точной дробью.

Математик 16 века Лудольф имел терпение вычислить его с 35 десятичными знаками. В 1946 – 1947 гг. два ученых независимо друг от друга вычислили 808 десятичных знаков числа π.

Приближенное значение π с точностью до пяти десятичных знаков можно запомнить по следующей строчке (по числу букв в слове): π ≈ 3, 1415926 - «это я знаю и помню прекрасно»

Мнемонические правила

Чтобы нам не ошибаться,

Надо правильно прочесть:

Три, четырнадцать, пятнадцать,

Девяносто два и шесть.

Неофициальный праздник «День числа Пи» отмечается 14 марта, которое в американском формате дат (месяц/день) записывается как 3.14, что соответствует приближённому значению числа π.

Ещё одной датой, связанной с числом π, является 22 июля, которое называется «Днём приближённого числа Пи» (англ. Pi Approximation Day), так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби является приближённым значением числа π ≈ 22/7 ≈ 3, 14

Итак, число π можно найти по формуле: π=С:d.

Индивидуальная работа в группе. Решение задач.

Объединить учащихся в однородные группы по 4 - 6 учеников, согласно выбранному уровню. Задание у всех групп одинаковое, но совместная работа с одноклассниками одного уровня позволит раскрыться каждому ученику.

Предложить ученикам выбрать уровень сложности задания по закреплению теоретического материала на более высоком уровне.

Раздать группам конверт с набором карточек, на каждом из которых написаны условия заданий. Предложить учащимся, определить по какой формуле вычислить ответ. В первый столбик записать номера заданий, которые на определение длины окружности по формуле: ,  где 3,14 . Во второй столбик -, где 3,14. В третий столбик -  и , где значение .

Приложение 3

Задание 1. Найдите длину окружности диаметра 3 см.

Задание 2.Найдите длину окружности радиуса  см.

Задание 3.Найдите длину окружности радиуса  м.

Задание 4.Найдите радиус окружности, если мм.

Задание 5. Найдите длину окружности диаметра 0,6 дм

Задание 6. Найдите радиус окружности, если мм.

Задание 7. Найдите радиус окружности, если см.

Задание 8.Найдите длину окружности радиуса 6 см.

Задание 9. Найдите длину окружности, если  см.

Задание 10. Найдите площадь круга, радиус которого равен 8 см. Число p округлите до десятых.

Задание 11. Длина окружности равна 0,628 м. Найдите диаметр круга.

Задание 12. Найдите площадь круга, радиус которого равен 6 м. Число p округлите до десятых.

Задание 13. Найдите длину окружности радиуса 2,3 м.

Задание 14. Найдите длину окружности, если ее диаметр равен 45 см. (Число p округлите до десятых.)

Задание 15. Найдите площадь круга, диаметр которого равен 4 м. (Число p округлите до десятых.)

Ключ

Предоставить достаточно времени для выполнения по 2 задания с каждого столбика. Ученики работают индивидуально, но имеют возможность спросить не понятные вопросы и сверить свои решения с одноклассниками по группе. Учитель помогает наиболее нуждающейся группе.

Проверить по ключу.

Коллективная работа. Решение задач из учебника.

Повторить теоретический материал с помощью презентации о шаре и сфере.

Шар — это пространственное тело. Внутри шар чем-либо заполнен. Поэтому у шара можно найти объем. Шар и сфера, подобно кругу и окружности, имеют центр, радиус и диаметр. Сфера — поверхность шара. У сферы можно найти площадь поверхности.

Для более продвинутых учеников можно дать задания на применение формул: Формула площади сферы: S = 4πR² . Формула объема шара: V =(4/3)πR³.

Для закрепления и оценки умения применять формулы пути и длины окружности, предложить устно вывести формулу пути, пройденного колесом.

Решить задачи по образцу задач из Приложения 4.

1.      Колесо на расстоянии 1256 м сделало 500 оборотов. Найдите диаметр колеса
(π ≈ 3,14). Ответ дайте в сантиметрах.

Решение:

n= 500 оборотов        Длина окружности колеса составляет  -составляет 1 оборот,

s= 1256 м                   Расстояние составляет n оборотов:  .

                                    1256 = 500∙3,14∙D  à  

Ответ:  = 80 см- диаметр колеса.

2.      Колесо на расстоянии 216,66 м сделало 69 оборотов. Найдите диаметр колеса
(π ≈ 3,14). Ответ округлите до сантиметров.

Ответ: 100 см.

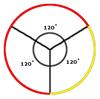
3.      Чему равна длина красной части окружности, если ее радиус равен
33 дм. Число π = 3.14. Ответ дайте в метрах. 

Ответ: 14 м.

4.      Диаметр колеса тепловоза равен 80 см. За 2 мин колесо делает 800 оборотов. Какова скорость тепловоза в километрах в час? Результат округлите до десятых км/час.

Ответ: 60,3 км/ч

5.      Площадь круга S=196π см². Какова длина радиуса данного круга?

Ответ: 14 см.

Ключ

Беседа. Рефлексия.

Обратить внимание на достижение целей обучения, которые поставлены вначале урока. урока.

- Что узнал, чему научился?

- Что осталось непонятным?

- Над чем необходимо поработать?

- Какой этап урока понравился больше всего?

Домашнее задание.

Знать определения окружности, круга, формулы и решить номера уровня В: №..№.

На уроке предусмотрена дифференциация в виде работы в однородных группах (одного уровня обучаемости). Ученики самостоятельно выбирают уровень сложности заданий. Предусмотрена проверка по ключу, в ходе которой ученики оценивают умение применять формулы. В ходе коллективной деятельности при решении задач устно оценивается умение применять теорию и ранее изученный материал при решении нового типа задач. Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу. Следить за осанкой учащихся.

Интернет-ресурсы:

http://school-assistant.ru/?predmet=matematika&theme=okruznost_i_krug

http://math-prosto.ru/?page=pages/circle/circle_length_number_pi.php

http://www.matematika-na.ru/6class/mat_6_24.php

http://www.yaklass.ru/p/matematika/6-klass/geometricheskie-figury-i-tela-simmetriia-na-ploskosti-13781/okruzhnost-i-krug-chislo-pi-dlina-okruzhnosti-ploshchad-kruga-13694/tv-082275f0-7fdb-41b3-b913-fb8e3a31c16c

Скачано с www.znanio.ru