26their connection with space and time properties

1)      Two balls X and Y are supported by long strings, as shown in figure.

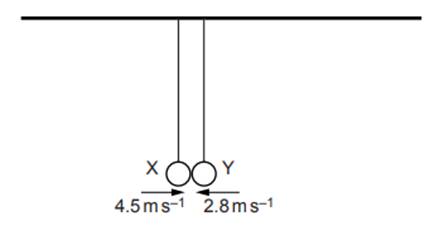
The balls are each pulled back and pushed towards each other. When the balls collide at the position shown in the figure, the strings are vertical. The balls rebound in opposite directions. Table shows data for X and Y during this collision.

a)      Define the mass M of ball Y.

b)      State and explain whether the collision is elastic or inelastic.

c)      Apply Newton’s laws for explanation of the equality in balls’ change in momentum.

Answers:

a)      M = 75 g = 0.075 kg

b)      Total kinetic energy just before collision is not equal to/bigger than the one after the collision, no energy conservation – collision is inelastic

c)      According to the Newton’s third law, force exerted by ball X is equal to but opposite to the force exerted by the ball Y. The time interval of the collision is the same for both balls. According to the Newton’s second law, the change in balls’ momentum is equal to product of force and time interval so it is equal for both balls

2)      A ball X and a ball Y are travelling along the same straight line in the same direction as shown in the figure.

After the collision the balls start to move differently as shown in the next figure.

Calculate:

a)      The total initial momentum of the system

b)      The velocity v

c)      The total initial kinetic energy of the balls

d)      Explain how can you check that collision is elastic.

Answers:

a)      0.53 N·s

b)      0.61 m/s

c)      0.145 J

d)      The total kinetic energy before collision of the balls is equal to the total kinetic energy after the collision.

3)      An object A of mass 4.2 kg and horizontal velocity 3.6 m/s moves towards object B as shown in the figure.

Object B of mass 1.5 kg is moving with a horizontal velocity of 1.2 m/s towards object A. the object collide and then both move to the right as shown in the figure below.

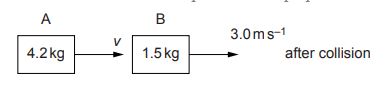
a)      Calculate the velocity v of object A after the collision.

b)      Determine whether the collision is elastic or inelastic.

Answers:

a)      2.1 m/s

b)      Initial kinetic energy is not equal to the final kinetic energy – collision is inelastic

4)      A ball is thrown against the vertical wall. Its path is shown in the figure.

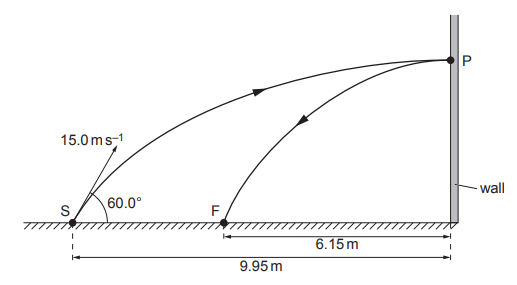
a)      Calculate the vertical height gained by the ball as it travels from point S to point P. 

b)      Calculate the time taken by the ball as it travels from point S to point P.

c)      Calculate the change of ball’s momentum as it rebouced from the wall.

Answers:

a)      8.61 m

b)      1.327 s

c)      – 0.73 N·s

5)      A stationary nucleus of mass 220u undergoes radioactive decay to produce a nucleus D of mass 216u and an α-particle of mass 4u, as illustrated.

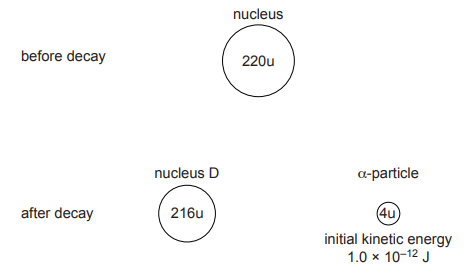
The initial kinetic energy of the α-particle is 1·10^-12 J.

a)      Explain why the initial velocities of the α-particle and nucleus D must be in opposite directions.

b)      Calculate the initial velocity of  theα-particle.

c)      Calculate the initial velocity of D nucleus.

Answers:

a)      Total momentum must be constant for isolated system of particles

b)      1.7·10⁷ m/s

c)      3.1·10⁵ m/s