27. ЦелыеМетодические рекомендации к уроку. Вариант 2

Методические рекомендации к уроку

Тема урока "Целые числа. Рациональные числа "

Цели обучения:

6.1.1.6

усвоить понятие целого числа;

6.5.2.3

использовать целые числа при описании величин;

6.1.1.8

усвоить понятие рационального числа;

6.1.2.9

изображать рациональные числа на координатной прямой;

6.1.2.11

изображать подмножества рациональных чисел с помощью кругов Эйлера-Венна.

Критерии оценивания

Учащийся:

знает:

·      понятие целого числа;

·      понятие рационального числа;

умеет:

·      использовать целые числа при описании величин;

·      изображать рациональные числа на координатной прямой;

·      изображать подмножества рациональных чисел с помощью кругов Эйлера-Венна.

·      применять  при решении задач.

Теоретический материал:

Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т. д. Элементы множества − это то, из чего это множество состоит, например, каждый ученик вашего класса есть элемент множества школьников. Множества обычно обозначают большими буквами: A, B, C, N, ..., а элементы этих множеств − аналогичными маленькими буквами: a, b, c, n, ... Существуют стандартные обозначения для некоторых множеств. Например,

·                     N − множество натуральных чисел;

·                     Z − множество целых чисел;

·                     Q− множество рациональных чисел.

Множество натуральных чисел N – это числа 1, 2, 3, 4 и т.д.

Определение: Числа, применяемые при счете, называют натуральными.

Любое натуральное число записывают с помощью десяти цифр: 0,1,2, 3, 4, 5, 6, 7, 8, 9.

Последовательность всех натуральных чисел называют натуральным рядом.

Нуль (0)-не натуральное число

1) Самое маленькое натуральное число – единица (1).

2) В натуральном ряду каждое следующее число на 1 больше предыдущего.

3) Натуральный ряд бесконечен, наибольшего числа в нем нет.

Множество целых чисел Z состоит из натуральных чисел, противоположных им (−1, −2, −3 и т.д.) и нуля 0.

Рациональные числа Q – числа вида , где aÎZ, bÎN (обыкновенные дроби).

Таким образом, существует включение: N содержится в Z, а Z содержится в Q.

.

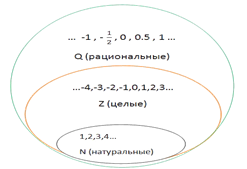
Целые и дробные числа (положительные и отрицательные) составляют множество рациональных чисел Q;

Каждое рациональное число может быть представлено в виде дроби с целым числителем и натуральным знаменателем, а каждая такая дробь представляет собой некоторое рациональное число.

Сумма двух рациональных чисел всегда рациональное число.

Разность двух рациональных чисел всегда рациональное число.

Произведение двух рациональных чисел всегда рациональное число.

Частное двух рациональных чисел – рациональное число, за исключением деления на ноль.

Есть версия, что название рациональных чисел связано с латинским словом «ratio» — разум.

Любое рациональное число можно представить в виде простой дроби: , где - целое число, - натуральное.

Любое целое число является рациональным, т.к. его можно записать в виде отношения со знаменателем 1. Например: ;  .

Любая отрицательная дробь будет рациональным числом. Например: : .

Смешанные числа так же являются рациональными числами. Например: : .

Десятичная дробь тоже является рациональным числом, т.к. : .

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание:

В диалоге с учащимися, вспомнить понятие множества, элементы множества, применяемые знаки для записи принадлежности элементов и включения подмножеств в множества: Î, Ì. Привести примеры натуральных чисел, целых чисел, повторить определения натуральных, целых чисел, обозначения этих множеств и свойства.

Выполнить Приложение 1.

Укажи все:

а) целые числа, расположенные на координатной прямой между числами −5,4  и 2,7;

б) натуральные числа, расположенные на координатной прямой между числами −5,4 и 2,7.

Ответ: а) между числами −5,4  и 2,7 находятся следующие целые числа:

−5, −4, −3, −2, −1, 0, 1, 2;

б) между числами −5,4  и 2,7 находится следующие натуральные числа: 1 и 2.

Кроме перечисленных чисел, есть и другие числа, которые можно перечислять бесконечно: дробные числа, десятичные дроби и целые ( положительные и отрицательные) вместе составляют множество.

Совместно с учащимися определить тему и цели урока, зону ближайшего развития.

Коллективная работа.

Высказать гипотезы о новом множестве чисел.

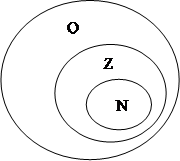
Целые и дробные числа (положительные и отрицательные) составляют множество рациональных чисел. Обозначают: Q.

Любое целое число  является рациональным числом, так как его можно записать в виде

Любое целое число является рациональным, т.к. его можно записать в виде отношения со знаменателем 1. Например: ;    .

Любая отрицательная дробь будет рациональным числом. Например: : .

Смешанные числа так же являются рациональными числами. Например: : .

Десятичная дробь тоже является рациональным числом, т.к. : .

Групповая работа.

Объединить учащихся в разноуровневые группы по 4 - 6 учеников.

1) Раздать каждой группе Приложение 2. Предложить выполнить задания.

Приложение 2

1) Представьте целое число в виде рационального числа: 4, 1, -1, -16, 0, 49.

2) Представьте дробь в виде рационального числа: ;   ; ; .

3) Представьте смешанное число в виде рационального числа: ; ; ; .

4) Представьте десятичную дробь в виде рационального числа: 0,35; -0,26; 1,23; -3,1.

Предоставить учащимся достаточно времени для выполнения заданий. Проверить ответы по ключам, сравнить, проверить правильность ответов.

2) Предлагается вывести свойства рациональных чисел.

Свойства рациональных чисел

·         Сумма двух рациональных чисел всегда рациональное число.

·         Разность двух рациональных чисел всегда рациональное число.

·         Произведение двух рациональных чисел всегда рациональное число.

·         Частное двух рациональных чисел – рациональное число, за исключением деления на ноль.

Учитель проходит по рядам, слушает, при необходимости корректирует гипотезы учащихся, проверяет и оценивает похвалой работу групп.

Открыть учебное пособие "Математика 6" (или раздать приложение 3) прочитать теорию к теме, сравнить свои гипотезы с текстом, оценить правильность рассуждений, при необходимости откорректироать информацию.

Старший группы оценивает вклад каждого, выставляя отметку.

Беседа. Рефлексия. «Рефлексивный ринг»

Что я знаю...          Сегодня я узнал…     

Что я умею...         Я научился…

Я теперь могу…   Я понял, что…      

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных группах (разного уровня обучаемости). Ученики, распределяя в паре задания, самостоятельно выбирают уровень сложности.

Предусмотрена самопроверка по ключу. В ходе групповой деятельности при выводе свойств оценивается умение применять теоретические знания.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

"Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

"Математика 6", Алдамуратова Т.А, Байшоланов Т.С.;

Самостоятельные и контрольные работы, Ершова А.П., Голобородько В.В. 

Интернет ресурсы:

http://www.yaklass.ru

https://school-assistant.ru

Скачано с www.znanio.ru