2.9 Серединный перпендикуляр, средняя линия треугольника.

Серединный перпендикуляр, средняя линия треугольника.

Повторяем теорию.

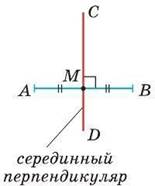
Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.

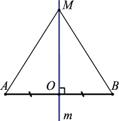
Свойства серединных перпендикуляров треугольника:

1.            Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

2.            (обратное утверждение) Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

3. 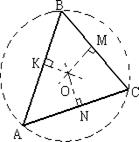           Точка           пересечения           серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.

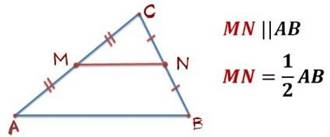Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

MN – средняя линия треугольника.

Свойство средней линии треугольника:

Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна её половине.

Проверяем себя.

Т1. Вставьте пропущенное слово:

а) Каждая точка серединного перпендикуляра                         от концов этого отрезка.

б)   Средней   линией   треугольника  называется  отрезок,  соединяющий

                двух его сторон.

в) Средняя линия треугольника                      одной из его сторон и равна половине этой стороны.

г) Серединные перпендикуляры к сторонам треугольника        в одной точке.

Ответ: а) равноудалена; б) середины; в) параллельна; г) пересекаются.

Т2. Выберите верное утверждение

а) Существует треугольник, в котором точка пересечения серединных перпендикуляров к его сторонам находится на стороне треугольника.

б)   Средняя   линия   треугольника   соединяет   середины   всех   сторон треугольника.

в)    Средняя   линия   треугольника   соединяет   вершину   с    серединой противолежащей стороны.

Ответ: а)

Т3. Выберите верное утверждение

1)  Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов отрезка.

2)  Средняя линия треугольника делит его на равновеликие фигуры.

3)       Через   заданную  точку   плоскости   можно   провести   только   один серединный перпендикуляр к стороне треугольника.

4)    Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, вписанной в треугольник.

Ответ: 1.

Решаем задачи.

1.     а) Найдите среднюю линию равностороннего треугольника, если его периметр равен 126.

Ответ: 21

б) Найдите среднюю линию равностороннего треугольника, если его периметр равен 69.

Ответ: 11,5

в) Найдите среднюю линию равностороннего треугольника, если его периметр равен 93.

Ответ: 15,5.

2.     а) Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 66, сторона BC равна 37, сторона AC равна 74. Найдите MN.

Ответ:37

б) Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 8, сторона BC равна 10, сторона AC равна 12. Найдите MN.

Ответ:6

в) Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 26, сторона BC равна 39, сторона AC равна 48. Найдите MN.

Ответ:24

3.            а) Периметр треугольника равен 30. Найдите периметр треугольника, вершинами которого являются середины сторон данного треугольника.

Ответ: 15

б) Периметр треугольника равен 48. Найдите периметр треугольника, вершинами которого являются середины сторон данного треугольника.

Ответ: 24

в) Периметр треугольника равен 63. Найдите периметр треугольника, вершинами которого являются середины сторон данного треугольника.

Ответ: 31,5.

4.               а) Периметр треугольника АВС равен 24,   DЕ - средняя линия треугольника, параллельная АВ. Найдите периметр треугольника СDЕ.

Ответ: 12

б)   Периметр   треугольника   АВС   равен   71,   DЕ   -    средняя   линия треугольника, параллельная АВ. Найдите периметр треугольника СDЕ.

Ответ: 35,5

в)   Периметр   треугольника   АВС   равен   102,   DЕ   -   средняя   линия треугольника, параллельная АВ. Найдите периметр треугольника СDЕ.

Ответ: 51

5. 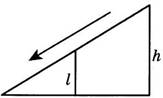           а) Столб подпирает детскую горку посередине. Найдите высоту 𝑃 столба, если высота ℎ горки равна 3.

Ответ: 1,5

б) Столб подпирает детскую горку посередине.

Найдите высоту 𝑃 столба, если высота ℎ горки равна 4.

Ответ: 2

в) Столб подпирает детскую горку посередине. Найдите высоту 𝑃 столба, если высота ℎ горки равна 2,2.

Ответ: 1,1.

6. 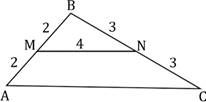           а) Используя данные на рисунке, найдите периметр треугольника АВС.

Ответ:18

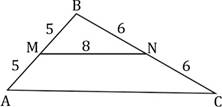б) Используя данные на рисунке, найдите периметр треугольника АВС.

Ответ: 38

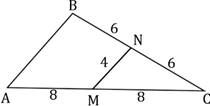в) Используя данные на рисунке, найдите периметр треугольника АВС.

Ответ: 36.

7.               а) Серединный перпендикуляр к стороне ВС треугольника АВС пересекает сторону АС в точке D. Найдите АD, если ВD=5 см, АС=8,5 см.

Ответ: 3,5

б) Серединный перпендикуляр к стороне ВС треугольника АВС пересекает сторону АС в точке D. Найдите АС, если ВD = 5 см, АD = 3,5 см.

Ответ: 8,5

в) Серединный перпендикуляр к стороне ВС треугольника АВС пересекает сторону АС в точке D. Найдите АD, если ВD=11,4 см, АС=14,6 см.

Ответ: 3,2.

Задачи с развернутым ответом.

1. В треугольнике ABC известно, что AB = BC, AC = 10. Из середины D стороны AB проведен перпендикуляр DE к стороне AB до пересечения со стороной BC в точке E. Периметр треугольника ABC равен 40. Найдите периметр треугольника AEC.

Ответ: 25

2.    Из середины гипотенузы восстановлен перпендикуляр до пересечения с катетом, и полученная точка соединена с концом другого катета отрезком, который делит угол треугольника в отношении 2:5 (меньшая часть – при гипотенузе). Найдите этот угол.

Ответ: 70°