
Методические рекомендации к уроку
Тема урока " Числовые промежутки. "
Цели обучения:
6.2.2.7
использовать обозначения для записи числовых промежутков;
6.2.2.8
изображать числовые промежутки;
Критерии оценивания
Учащиеся
знают:
□ как правильно читать неравенства;
□ как записывать, используя математическую символику, неравенства;
умеют
□ -изображать числовые промежутки;
□ использовать обозначения для записи числовых промежутков.
Теоретический материал
Определение:
Множество чисел, расположенных между числами ![]() и
и
![]() , называют числовым промежутком.
, называют числовым промежутком.
Ход урока
Организационный момент. Актуализация опорных знаний.
Проверить домашнее задание.
Решить задания на повторение.
Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".
Индивидуальная работа. Для закрепления и оценки усвоения пройденного материала предложить учащимся задания подобные заданиям Приложения 1. Каждый выполняет самостоятельно.

![]()
а) сумму; произведение; разность.
Решение:

3) а) Пусть а см – сторона квадрата, тогда Р = 4а см – периметр квадрата.
5,1 ≤ а ≤ 5,2;
Найти Р.
Решение:
5,1 · 4 ≤ 4а ≤ 5,2 · 4; 20,4 ≤ 4а ≤ 20,8.
б) Пусть Р
см – периметр квадрата, тогда ![]() см – сторона квадрата.
см – сторона квадрата.
15,6 ≤ Р ≤ 15,8;
Найти ![]() .
.
15,6 : 4 ≤ ≤ 15,8 : 4; 3,85 ≤ а ≤ 3,95.
О т в е т: а) 20,4 ≤ 4а ≤ 20,8; б) 3,85 ≤ а ≤ 3,95.
4) Прочитайте неравенство и перечислите несколько значений переменной, удовлетворяющее данному неравенству:
А) x > 3; Б) x £ 12; В) -8< x £ 1,8
После окончания выполнения, попросить обменяться тетрадями с соседом. Взаимопроверка по ключу. Собрать информацию о выполнении. Разобрать один из вариантов.
Работа с классом. Ввод новой темы: Обычно решая задания, мы озвучиваем конкретный ответ, или несколько ответов, или утверждаем что нет ответа. В задании 4) Прочитайте неравенство и перечислите несколько значений переменной, удовлетворяющее данному неравенству: А) x > 3; Б) x £ 12; В) -8< x £ 1,8 - у каждого свой ответ.
Мы не ответили сколько всего решений и конкретно какие.
Математические модели бывают не только алгебраические (в виде числового равенства, уравнения, неравенства), но и словесные (в виде словесного описания реальной ситуации), графические (в виде схемы, графика, чертежа). Учащиеся уже знакомы со всеми этими видами моделей. Напоминаем, что алгебраическую модель ещё называют аналитической, а графическую – геометрической. Чтобы свободно оперировать любыми видами математических моделей, нужно учиться переходить от одного из них к другому.
Н а п р и м е р:
|
Словесная модель № 1 |
Аналитическая |
Геометрическая |
Словесная модель № 2 |
|
b больше а |
b > a |
|
Точка с координатой b лежит правее точки с координатой а |
Если изобразим на числовом луче решение неравенства - это будет точный ответ, так как решений бесконечно много.
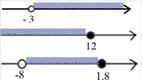
Так изображается полный ответ на вопрос задания 4. Это геометрическое изображение ответа на вопрос о решении неравенств, называемые числовыми промежутками.
Определение:
Множество чисел, расположенных между числами ![]() и
и
![]() , называют числовым промежутком.
, называют числовым промежутком.
У каждого промежутка есть свое название.
Виды числовых промежутков: интервал, отрезок, полуинтервал, луч, открытый луч.
Так как у неравенств бесконечное множество решений, записать все невозможно. Решение можно отобразить на оси координат. Отображённое на оси координат решение неравенства можно записать в виде числового интервала.
|
Вид неравенства и обозначение точки на оси координат (закрашенная или пустая) |
Запись принадлежности конечной точки интервалу |
|
≤ или ≥∙(конечная точка включена) |
[или] - квадратные скобки |
|
< или > (конечная точка не включена) |
( или ) - круглые скобки |
Общий вид на таблице.
Приложение 2
|
|
Читают |
|
Промежуток от |
|
|
Промежуток от |
|
|
Промежуток от |
|
|
Промежуток от Промежуток от
минус бесконечности до |
|
|
Промежуток от Промежуток от
минус бесконечности до |
С целью экономии времени, можно после объяснения и разбора каждого случая, раздать учащимся таблицу для пользования.
Первичное закрепление. Особое внимание уделяем:
– правильным формулировкам;
– верному использованию круглых и квадратных скобок при обозначении числового промежутка;
– верному использованию светлых кружков («выколотых» точек) и тёмных при изображении числовых промежутков на координатной прямой.
Для отработки навыков умения работать с таблицей, решить следующее задание.
Для заданного неравенства прочитайте данные числовые промежутки, изобразите на координатной прямой и запишите промежуток, пользуясь таблицей.
а) х
≥ –2; ![]() ; [–2; +∞).
; [–2; +∞).
б) х <
–5; ![]() ; (–∞; –5).
; (–∞; –5).
в) 2 < х
≤ 6,1; ![]() ; (–2; 6,1].
; (–2; 6,1].
Дальнейшее закрепление провести в руппах.
Групповая работа. Объединить учащихся в разноуровневые малые группы. Раздать каждой группе карточки с заданиями.
Приложение 3
1) Запишите промежуток в виде неравенства, назовите промежутки, изображенные на рисунке.
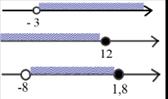
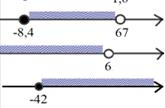
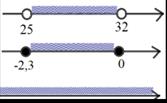
2) Изобразить промежутки на координатной прямой.
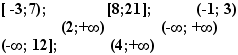
3) Запишите и обозначьте данные числовые промежутки:
а)
интервал от -2 до 5;
б) отрезок от 11 до 24;
в) полуинтервал от 5 до 12, включая 5;
г) луч от 5 до +∞
4. Задайте неравенством числовой промежуток:
а) 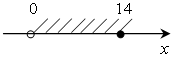 ж) х
ж) х ![]() [2;7,3];
[2;7,3];
б) 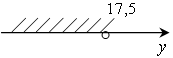 з)
y
з)
y ![]() (–∞; 100);
(–∞; 100);
в) 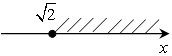 и)
х
и)
х ![]() (–8,3; 0];
(–8,3; 0];
г) 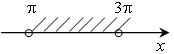 к)
y
к)
y ![]() (0; +∞);
(0; +∞);
д) 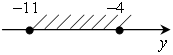 л)
х
л)
х ![]() (–15; –4);
(–15; –4);
е) 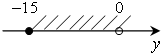 м)
y
м)
y ![]() [–60; 100).
[–60; 100).
Учитель проходит по рядам, слушает, при необходимости задает дополнительные вопросы, корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.
Предоставить учащимся достаточно времени для выполнения заданий.
Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям.
Каждая группа демонстрирует свой результат выполнения заданий.
Старший группы оценивает вклад каждого, выставляя отметку.
Беседа. Рефлексия.
|
На уроке мне понравилось…. |
На уроке мне не понравилось…. |
|
На уроке понял
|
На уроке не понял
|
Домашнее задание. Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.
На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).
Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.
Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.
Литература:
1. "Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;
2. "Математика 6", Алдамуратова Т.А, Байшоланов Т.С.; Алматы. «Атамура». 2011 год.
3. Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192
4. Г.В.Дорофеев, Л.Г. Петерсон. Математика. 6 класс. Часть 3. Москва. Ювента. 2011 год.
5. Математика - 6» автор Н.Я.Виленкин, Жохов В.И, Чесноков А.С. и др., Москва «Мнемозина», 2010г.
Интернет ресурсы:
1. http://www.yaklass.ru
2. https://school-assistant.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.