3.23 Касательная и секущая к окружности

Касательная и секущая к окружности.

Повторяем теорию.

Окружность – это множество точек плоскости, расположенных на одинаковом расстоянии от данной точки (центра).

Радиус – это отрезок, соединяющий центр окружности с любой точкой окружности.

Два радиуса, лежащие на одной прямой, образуют диаметр. Хорда – это отрезок, соединяющий две точки окружности.

Диаметр – хорда, проходящая через центр окружности

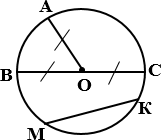
О – центр

ОА, ОВ, ОС - радиусы ВС – диаметр

МК, ВС – хорды

Касательная – это прямая, имеющая с окружностью только одну общую точку.

Секущая – это прямая, имеющая с окружностью две общие точки.

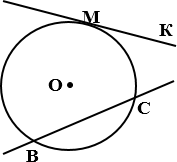
МК – касательная ВС – секущая

Утверждения о касательных и секущих

1.      Расстояние от центра окружности до касательной равно радиусу.

2.      Касательная перпендикулярна радиусу, проведенному в точку касания.

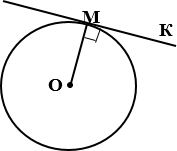
Окружность с центром О,

М – точка касания, следовательно, ОМ=R, ОМ ⊥ МК.

3.     Если прямая перпендикулярна радиусу и проходит через конец этого радиуса, лежащий на окружности, то она является касательной. (признак касательной).

Окружность с центром О, ОМ – радиус, МК ⊥ ОМ, следовательно, МК – касательная.

4.      Расстояние от центра окружности до секущей меньше радиуса.

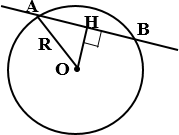Окружность с центром О, R- радиус, АВ – секущая, ОН ⊥ АВ, следовательно, ОН<R.

5.     Если расстояние от центра окружности до прямой меньше радиуса, то эта прямая – секущая. Если расстояние больше радиуса, то эта прямая не имеет с окружностью общих точек.

6.     Отрезки касательных, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через центр окружности и эту общую точку.

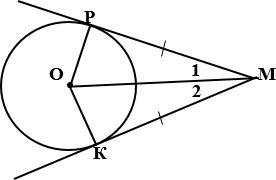Окружность с центром О, МР и МК – касательные, К и Р точки касания,                          следовательно, МР=МК, ∠1 = ∠ 2,

ОР² + РМ² = ОМ².

7.     Если касательная пересекается с секущей, то квадрат отрезка касательной равен произведению расстояний от общей точки до точек пересечения секущей с окружностью.

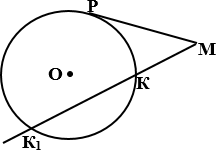Окружность с центром О, МК – секущая,

МР – касательная,

Р – точка касания, следовательно, МР² = МК • МК₁.

8. 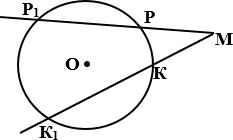    (дополнительно) Произведение всей секущей на ее внешнюю часть для данной точки и данной окружности постоянно.

Секущие МР и МК, следовательно, МР • МР₁ = МК • МК₁.

Проверяем себя.

Т1. Вставьте пропущенное слово:

а)   Отрезок,   соединяющий    центр    окружности    с    какой-либо        точкой окружности, называется                              окружности.

б)  Хорда,      проходящая      через      центр      окружности,      называется

                            .

в) Отрезок, соединяющий две точки окружности, называется                         . г)   Центр окружности является                                 любого диаметра.

Ответ: а) радиусом; б) диаметром; в) хордой; г) серединой

Т2. Выберите верное утверждение Касательной к окружности называется:

а)     Прямая, которая пересекает окружность.

б)    Прямая, имеющая с окружностью только одну общую точку. в)      Прямая, имеющая с окружностью общие точки.

г)     Отрезок, имеющий с окружностью только одну общую точку.

Ответ: б)

Т3. Выберите верное утверждение Признак касательной к окружности гласит:

а)     Касательная к окружности перпендикулярна радиусу, проведенному в точку касания

б)    Если прямая проходит через конец радиуса, лежащий на окружности, то она является касательной.

в)     Если  прямая  имеет   с   окружностью общие   точки,  то   она является касательной.

г)     Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна этому радиусу, то она является касательной.

Ответ: г).

Решаем задачи.

1. 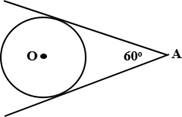                а) Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.

Ответ: 3

б) Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.

Ответ: 16

в) Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 6.

Ответ: 12.

2. 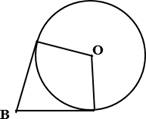                а) Из точки В проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки В до точки касания с окружностью, если угол между касательными равен  120°,  а  расстояние  от  точки В до точки О равно 26.

Ответ: 13

б) Из точки В проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки В до точки касания с окружностью, если угол между касательными равен 90°, а радиус окружности равен 17.

Ответ: 17

в) Из точки В проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки В до точки касания с окружностью, если угол между касательными равен 120°, а расстояние от точки В до точки О равно 38.

Ответ: 19

3. 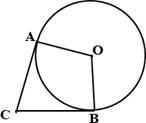              а) В угол С величиной 83^o вписана окружность, которая касается сторон угла в точках А и В, точка О – центр окружности. Найдите величину угла АОВ. Ответ дайте в градусах.

Ответ: 97

б) В угол С величиной 127^o вписана окружность, которая касается сторон угла в точках А и В, точка

О – центр окружности. Найдите величину угла АОВ. Ответ дайте в градусах.

Ответ: 53

в) В угол С величиной 56^o вписана окружность, которая касается сторон угла в точках А и В, точка О – центр окружности. Найдите величину угла АОВ. Ответ дайте в градусах.

Ответ: 124

4. 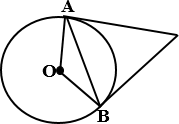                а) Касательные в точках A и B к окружности с центром O пересекаются под углом 24°. Найдите угол ABO. Ответ дайте в градусах.

Ответ: 12

б) Касательные в точках А и В к окружности с центром О пересекаются под углом 76°. Найдите угол АВО. Ответ дайте в градусах.

Ответ: 38

в) Касательные в точках А и В к окружности с центром в точке О

пересекаются под углом 82°. Найдите угол АВО. Ответ дайте в градусах.

Ответ: 41

5. 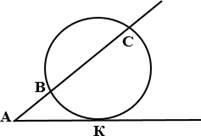                а) Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=4, AC=64. Найдите AK.

Ответ: 16

б)   Через   точку   A,   лежащую   вне

окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=2, BC=6. Найдите AK.

Ответ: 4

в) Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=6, AC=54. Найдите AK.

Ответ: 18

6. 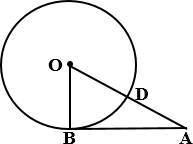               а) Отрезок AB = 48 касается окружности радиуса 14 с центром O в точке B. Окружность пересекает отрезок AO в точке

D. Найдите AD.

Ответ: 36.    б) Отрезок AB = 32 касается окружности радиуса 24 с центром O в точке

B. Окружность пересекает отрезок AO в точке D. Найдите AD.

Ответ: 16

в) Отрезок AB = 51 касается окружности радиуса 68 с центром O в точке

B. Окружность пересекает отрезок AO в точке D. Найдите AD.

Ответ: 17

7. 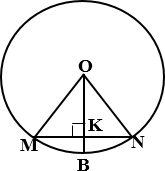                а) Радиус OB окружности с центром в точке O пересекает хорду MN в её середине — точке K. Найдите длину хорды MN, если KB = 1 см, а радиус окружности равен 13 см.

Ответ: 10

б) Радиус OB окружности с центром в точке O пересекает хорду MN в её середине — точке K. Найдите длину хорды MN, если KB = 1 см, а радиус окружности равен 5 см.

Ответ: 6

в) Радиус OB окружности с центром в точке O пересекает хорду MN в её середине — точке K. Найдите длину хорды MN, если KB = 1 см, а радиус окружности равен 25 см.

Ответ: 14

Задачи с развернутым ответом

1.     Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=12, а расстояния от центра окружности до хорд AB и CD равны соответственно 8 и 6.

Ответ: 16

2.     Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=30, CD=40, а расстояние от центра окружности до хорды AB равно 20.

Ответ: 15

3.     Через точку A, находящуюся вне окружности на расстоянии, 7 от её центра, проведена прямая, пересекающая окружность в точках B и C. Найдите радиус окружности, если известно, что AB = 3, BC = 5.

Ответ: 5