3.24 Хорды и дуги

Хорды и дуги.

Повторяем теорию.

Хорда – это отрезок, концы которого лежат на окружности.

Дуга – это часть окружности, соединяющая две точки. Дуга называется полуокружностью, если хорда, соединяющая ее концы, является диаметром.

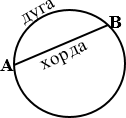АВ – хорда

ÈAB – дуга АВ

Свойства хорд и дуг

1. 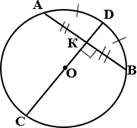    Диаметр, перпендикулярный хорде, делит хорду и стягивающую ее дугу пополам.

Окружность с центром О, СD – диаметр,

АВ – хорда,

АВ⊥СD, следовательно, АК = КВ,

ÈАD = È DВ

2.     Серединный перпендикуляр к хорде проходит через центр окружности. Окружность с центром в точке О, АВ – хорда, АВ⊥ С𝐷, АВ ∩ CD = K, АК

= КВ, следовательно, О ∈ CD.

3. 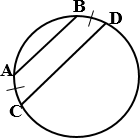    Дуги        окружности,       заключенные между параллельными хордами, равны.

АВ и СD – хорды, АВ ∥ СD ⇔ ÈАС = ÈВD.

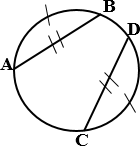
4.      Равные хорды стягивают равные дуги (верно и обратное утверждение).

АВ и СD – хорды, АВ = СD ⇔ ÈАВ = ÈСD.

5. 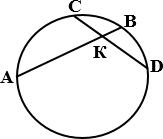    Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

СD и ВА – хорды, К – точка их пересечения, ⟹

СК ∙ КD = АК ∙ КВ.

6. 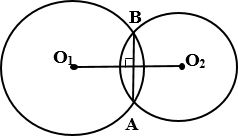    (дополнительно)      Общая      хорда      пересекающихся окружностей перпендикулярна прямой, содержащей центры этих окружностей.

О₁ и О₂ – центры окружностей, А и В – точки их пересечения, ⇒ АВ ⊥ О₁О₂.

Проверяем себя.

Т1. Вставьте пропущенное слово

а) Любые две точки окружности делят ее на две части. Каждая из этих частей называется                      окружности.

б) Дуги окружности, заключенные между                            хордами, равны.

в) Диаметр,                                                 хорде, делит хорду и стягивающую ее дугу пополам.

г) Серединный перпендикуляр к хорде проходит через                                 .

д)                                        - дуга окружности, если отрезок, соединяющий ее концы, является диаметром.

Ответ:   а)   дугой;   б)   параллельными;   в)   перпендикулярный;   г)            центр окружности; д) полуокружность.

Т2. Выберите верные утверждение Хорда окружности – это:

а)  Отрезок, который меньше диаметра, но больше радиуса. б)  Отрезок, который не проходит через центр окружности. в)  Отрезок, соединяющий две точки окружности.

г)   Часть окружности, ограниченная двумя точками окружности.

Ответ: в).

Т3. Выберите верные утверждение

а)   Если две дуги равны, то стягивающие их хорды параллельны. б) Если две хорды параллельны, то стягиваемые ими дуги равны. в) Перпендикулярные хорды равны.

г)   Если две дуги равны, то стягивающие их хорды равны.

Ответ: г).

Решаем задачи.

1. 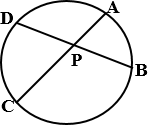              а)     Хорды AC и BD окружности   пересекаются   в точке P, BP=4, CP=12, DP=21. Найдите AP.

Ответ: 7

б) Хорды AC и BD окружности пересекаются в точке

P, BP=8, CP=24, DP=18. Найдите AP.

Ответ: 6

в) Хорды AC и BD окружности пересекаются в точке P, BP=10, CP=8, DP=12. Найдите AP.

Ответ: 15

2.        а) Прямая касается окружности в точке K. Точка O – центр окружности. Хорда КМ образует с касательной угол, равный 7°. Найдите величину угла ОМК. Ответ запишите в градусах.

Ответ: 83.

б) Прямая касается окружности в точке K. Точка O – центр окружности. Хорда КМ образует с касательной угол, равный 38°. Найдите величину угла ОМК. Ответ запишите в градусах.

Ответ:52

в) Прямая касается окружности в точке K. Точка O – центр окружности. Хорда КМ образует с касательной угол, равный 42°. Найдите величину угла ОМК. Ответ запишите в градусах.

Ответ: 48

3. 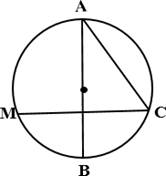               а)   Через   точку   A,   лежащую   на  окружности, проведены диаметр AB и хорда AC, причём AC = 8 и

∠ВАС = 30° Найдите хорду CM, перпендикулярную

AB.

Ответ: 8.

б) Через точку A, лежащую на окружности, проведены диаметр AB и хорда AC, причём AC = 10 и ∠САВ = 30 ° Найдите хорду CM, перпендикулярную AB.

Ответ: 10

в) Через точку A, лежащую на окружности, проведены диаметр AB и хорда AC, причём AC = 17 и ∠ВАС = 30° Найдите хорду CM, перпендикулярную AB.

Ответ: 17

4. 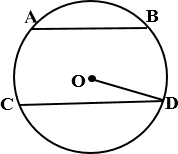           а)   AB   и    CD   –   две   параллельные   хорды, расположенные по разные стороны от центра O окружности радиуса 15. AB = 18, CD = 24. Найдите расстояние между хордами.

Ответ: 21

б) AB и CD – две параллельные хорды, расположенные по разные стороны от центра O окружности радиуса 13. AB = 24, CD = 10.

Найдите расстояние между хордами.

Ответ: 17

в) AB и CD – две параллельные хорды, расположенные по разные стороны от центра O окружности радиуса 25. AB = 48, CD = 14.

Найдите расстояние между хордами.

Ответ: 31

5. 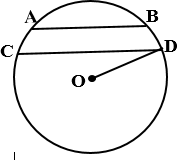            а) Две параллельные хорды AB и CD расположены по одну сторону от центра O окружности радиуса

30. AB = 36, CD = 48. Найдите расстояние между хордами.

Ответ: 6

б) Две параллельные хорды AB и CD расположены по одну сторону от центра O окружности радиуса 25. AB = 14, CD = 48. Найдите расстояние между хордами.

Ответ: 17

в) Две параллельные хорды AB и CD расположены по одну сторону от центра O окружности радиуса 29. AB = 40, CD = 42. Найдите расстояние между хордами.

Ответ: 1

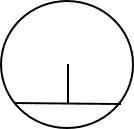
6.             а) Длина хорды окружности равна 40, а расстояние от центра окружности до этой хорды равно 48. Найдите диаметр окружности.

Ответ: 104.

б) Длина хорды окружности равна 12, а расстояние от центра окружности до этой хорды равно 8. Найдите диаметр окружности.

Ответ: 20

в) Длина хорды окружности равна 88, а расстояние от центра окружности до этой хорды равно 33. Найдите диаметр окружности.

Ответ: 110

7. 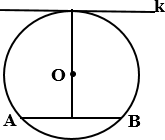     а) Радиус окружности с центром в точке O равен 65, длина хорды AB равна 126. Найдите расстояние от хорды AB до параллельной ей касательной k.

Ответ: 81

б) Радиус окружности с центром в точке O равен 82, длина хорды AB равна 36. Найдите расстояние от хорды AB до параллельной ей касательной k.

Ответ: 162

в) Радиус окружности с центром в точке O равен 90, длина хорды AB равна

144. Найдите расстояние от хорды AB до параллельной ей касательной k. Ответ: 144.

Задачи с развернутым ответом

1.     Две хорды окружности взаимно перпендикулярны. Докажите, что расстояние от точки их пересечения до центра окружности равно расстоянию между их серединами.

(Указание: использовать свойство 1).

2.     Хорды AC и BD взаимно перпендикулярны и пересекаются в точке M. Известно, что AM = 3, BM = 4 и CM = 6. Найдите хорду CD.

Ответ: 7,5

3.     В данном круге проведены две равные параллельные хорды, расстояние между которыми равно радиусу данного круга. Найдите острый угол между прямыми, соединяющими концы хорд.

Ответ: 60.

4.     Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В. Найдите диаметр окружности, если АВ = 1, АС = 5.

Ответ: 4,8

5.     Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В. Найдите АС, если диаметр окружности равен 15, а АВ = 4.

Ответ: 16