
Площадь плоской фигуры. Площадь параллелограмма.
Повторяем теорию.
1. Понятие площади известно каждому из жизненного опыта.
В геометрии площадь плоской фигуры - это числовая характеристика, показывающая размер этой фигуры.
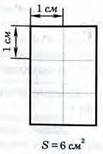 Площадь
многоугольника - величина
занимаемой им части
плоскости.
Площадь
многоугольника - величина
занимаемой им части
плоскости.
Обычно площадь оценивают квадратами со стороной в 1единичный отрезок, накладывая сетку из таких квадратов на фигуру. Поэтому исторически площадь называли квадратурой.
2. Единицы измерения площади:
1 квадратный метр (м2) = 100 дм2 (10дм ∙10дм) = 10000 см2 (100см∙100см) = 1000000 мм2(1000мм∙1000мм).
1 квадратный километр (км2) = 1000000 (м2). 1 ар (сотка) = 100(м2).
1 гектар (га) = 10000(м2) = 100(ар) = 0,01(км2).
3.Свойства площадей плоских фигур:
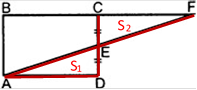 Равные многоугольники
имеют равные площади. S1
= S2
Равные многоугольники
имеют равные площади. S1
= S2
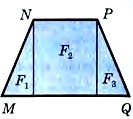 Многоугольники,
имеющие равные площади, называют равновеликими. Если многоугольник составлен из нескольких многоугольников, то
его площадь равна сумме площадей этих многоугольников.
Многоугольники,
имеющие равные площади, называют равновеликими. Если многоугольник составлен из нескольких многоугольников, то
его площадь равна сумме площадей этих многоугольников.
![]() S
MNPQ = 𝑠F1 + 𝑠F2 + 𝑠F3
S
MNPQ = 𝑠F1 + 𝑠F2 + 𝑠F3
 Площадь
квадрата равна квадрату
его стороны.
Площадь
квадрата равна квадрату
его стороны.
S = a∙a = a2 а
Площадь выпуклого четырехугольника равна половине произведения длин его диагоналей на синус острого угла между ними.
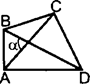
![]() S = 1
АС BD sin 𝛼
S = 1
АС BD sin 𝛼
2
AC и BD – диагонали
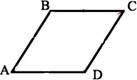 Параллелограмм – это четырехугольник, противоположные стороны которого попарно
параллельны.
Параллелограмм – это четырехугольник, противоположные стороны которого попарно
параллельны.
АВ║CD, BC║AD
Площадь параллелограмма.
|
Рисунок |
Определение |
Формула |
|
|
Площадь параллелограмма равна произведению его стороны и высоты, проведенной к этой стороне. |
S = a ha = b hb |
|
|
Площадь параллелограмма равна произведению его смежных сторон на синус угла между ними |
S = АВ∙АD ∙sin∠𝐴 = =BA∙ BC ∙ sin∠𝐵 |
|
α α |
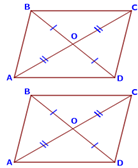
Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними |
S = 1 АС ∙ BD ∙ sin 𝛼 2 |
![]()
 Проверяем себя.
Проверяем себя.
Т1. Какие из следующих утверждений верны?
а) Площадь выпуклого четырехугольника равна произведению его диагоналей на синус острого угла между ними.
б) Площадь любого параллелограмма равна произведению длин его сторон.
в) Площадь параллелограмма равна произведению его смежных сторон на синус угла между ними.
г) Площадь квадрата равна квадрату его стороны.
Ответ в), г).
Т2. Выберите верные утверждения.
1) Площадь параллелограмма равна произведению его основания на высоту.
2) Площадь квадрата равна половине квадрата его диагонали.
3) Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
4) Все равносторонние треугольники имеют равные площади.
Ответ 123.
Т3. Какие из следующих утверждений верны?
1) Любой параллелограмм с прямыми углами является прямоугольником.
2) Площадь квадрата равна сумме двух его смежных сторон.
3) Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.
4) Равные треугольники имеют равные площади.
Ответ 134.
Решаем задачи.
1. Найдите площадь параллелограмма, изображённого на рисунке.
|
а)
Ответ 28 |
б)
Ответ 20 |
в)
Ответ 44 |
2.
![]() а)
Площадь параллелограмма равна 40, а две его стороны равны 5 и 10. Найдите
его высоты. В ответе укажите
большую высоту.
а)
Площадь параллелограмма равна 40, а две его стороны равны 5 и 10. Найдите
его высоты. В ответе укажите
большую высоту.
Ответ 8.
![]() б) Площадь
параллелограмма равна 36, а две его стороны
равны 6 и 12.
б) Площадь
параллелограмма равна 36, а две его стороны
равны 6 и 12.
Найдите его высоты. В ответе укажите большую высоту.
Ответ 6.
![]() в) Площадь
параллелограмма равна 60, а две его стороны
равны 4 и 20.
в) Площадь
параллелограмма равна 60, а две его стороны
равны 4 и 20.
Найдите его высоты. В ответе укажите большую высоту.
Ответ 15.
3. а) Стороны параллелограмма равны 3 и 13, а синус одного из углов параллелограмма равен 2/3. Найдите площадь параллелограмма.
Ответ 26.
б) Стороны параллелограмма равны 8 и 10, а синус одного из углов параллелограмма равен 0,05. Найдите площадь параллелограмма.
Ответ 4.
в) Стороны параллелограмма равны 12 и 5, а синус одного из углов параллелограмма равен 1/3. Найдите площадь параллелограмма.
Ответ 20.
4.
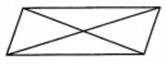 а) Диагонали параллелограмма равны 7 и 24, а угол между ними равен 300. Найдите
площадь параллелограмма.
а) Диагонали параллелограмма равны 7 и 24, а угол между ними равен 300. Найдите
площадь параллелограмма.
Ответ 42.
б) Диагонали параллелограмма равны 10 и 26, а угол между ними равен
300. Найдите площадь параллелограмма.
Ответ 65.
2) Диагонали параллелограмма равны 12 и 17, а угол между ними равен
300. Найдите площадь параллелограмма.
Ответ 51.
5.
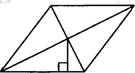 а) Сторона параллелограмма равна 7, а расстояние от точки пересечения диагоналей параллелограмма до нее равно
3. Найдите площадь параллелограмма.
а) Сторона параллелограмма равна 7, а расстояние от точки пересечения диагоналей параллелограмма до нее равно
3. Найдите площадь параллелограмма.
Ответ 42.
б) Сторона параллелограмма равна 11, а расстояние от точки пересечения диагоналей параллелограмма до нее равно 4. Найдите площадь параллелограмма.
Ответ 88.
в) Сторона параллелограмма равна 8, а расстояние от точки пересечения диагоналей параллелограмма до нее равно 3,5. Найдите площадь параллелограмма.
Ответ 56.
6. 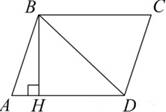 а) Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 2 и HD =
6. Диагональ параллелограмма BD равна 10. Найдите площадь
параллелограмма.
а) Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 2 и HD =
6. Диагональ параллелограмма BD равна 10. Найдите площадь
параллелограмма.
Ответ 64.
б) Высота BH параллелограмма ABCD делит его
сторону AD на отрезки AH = 2 и HD = 5. Диагональ параллелограмма BD равна
13. Найдите площадь параллелограмма.
Ответ 84.
в) Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 7 и HD = 15. Диагональ параллелограмма BD равна 25. Найдите площадь параллелограмма.
Ответ 440.
7.
![]() а) Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов равен 60°. Найдите
площадь параллелограмма, деленную
на √3.
а) Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов равен 60°. Найдите
площадь параллелограмма, деленную
на √3.
Ответ 30.
![]() б) Одна из сторон
параллелограмма равна 13, другая равна 24, а один из углов равен 450. Найдите площадь параллелограмма, деленную
на √2.
б) Одна из сторон
параллелограмма равна 13, другая равна 24, а один из углов равен 450. Найдите площадь параллелограмма, деленную
на √2.
Ответ 156.
![]() в) Одна из сторон
параллелограмма равна 30, другая равна 9, а один из углов равен
450. Найдите площадь параллелограмма, деленную на √2.
в) Одна из сторон
параллелограмма равна 30, другая равна 9, а один из углов равен
450. Найдите площадь параллелограмма, деленную на √2.
Ответ 135.
Задачи с развернутым ответом.
1.
![]() Площадь параллелограмма ABCD равна 180. Точка E — середина стороны AB. Найдите площадь трапеции BCDE.
Площадь параллелограмма ABCD равна 180. Точка E — середина стороны AB. Найдите площадь трапеции BCDE.
Ответ: 135 .
2.
![]() Площадь параллелограмма ABCD равна 32. Точка E — середина стороны AB. Найдите площадь трапеции
BCDE.
Площадь параллелограмма ABCD равна 32. Точка E — середина стороны AB. Найдите площадь трапеции
BCDE.
Ответ: 24.
Пример решения задачи с развернутым ответом.
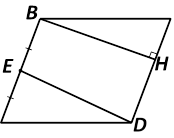
![]() 1. Площадь параллелограмма ABCD равна 180. Точка
E — середина стороны AB. Найдите площадь трапеции BCDE.
1. Площадь параллелограмма ABCD равна 180. Точка
E — середина стороны AB. Найдите площадь трапеции BCDE.
 Решение
Решение
С
Опустим из вершины B высоту BH на сторону CD, эта высота общая для параллелограмма ABCD и для трапеции BCDE.
SABCD = CD × BH =180 A
CD + CD
3CD
SBCDE
= 2 × BH = × BH .
![]() 2 4
2 4
Т.к. CD × BH =180 , то
Ответ: 135.
SBCDE
= 3×180 .
![]()
![]() 4
4
Задание 2 решается аналогичным способом.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.