3.26 Площадь прямоугольника, ромба, квадрата.

Площадь прямоугольника, ромба, квадрата.

Повторяем теорию.

Ромб – это параллелограмм, у которого все стороны равны.

Прямоугольник – параллелограмм, у которого все углы прямые.

Квадрат – это                прямоугольник,  у   которого  все   стороны равны.

Площади.

Решаем устно.

1)          Стороны    прямоугольника    равны    4    и    6.    Найдите    площадь прямоугольника.

2)  Сторона квадрата равна 4√2. Найдите площадь квадрата.

Ответ 32.

3)     Сторона ромба равна 8, а синус угла между сторонами равен 0,5. Найдите площадь ромба.

Ответ 32.

Проверяем себя.

Т1. Какие из следующих утверждений верны?

1)        Площадь   ромба   равна   произведению   его   стороны   на   высоту, проведѐнную к этой стороне.

2)    Площадь прямоугольника равна половине произведения квадрата его диагонали на синус угла между диагоналями.

3)  Площадь ромба равна произведению его диагоналей.

4)  Площадь параллелограмма равна произведению длин его сторон.

Ответ 12.

Т2. Какие из следующих утверждений верны?

1)  Существует ромб, который не является квадратом.

2)  Площадь прямоугольника равна произведению длин его сторон.

3)        Площадь   ромба   равна   произведению   его   стороны   на   высоту, проведенную к этой стороне.

Ответ 13.

Т3. Какие из следующих утверждений верны?

1)   Площадь ромба равна произведению двух его смежных сторон на синус угла между ними.

2)  Площадь квадрата равна половине квадрата его диагонали.

3)  Сумма углов любого треугольника равна 180°.

4)  Все квадраты имеют равные площади.

Ответ 123.

Решаем задачи

1.     а) Периметр квадрата равен 20. Найдите площадь квадрата.

Ответ 25.

б) Периметр квадрата равен 28. Найдите площадь квадрата.

Ответ 49.

в) Периметр квадрата равен 84. Найдите площадь квадрата.

Ответ 441.

2.     а) Найдите площадь квадрата, если его диагональ равна 3.

Ответ 4,5.

б) Найдите площадь квадрата, если его диагональ равна 40.

Ответ 800.

в) Найдите площадь квадрата, если его диагональ равна 5.

Ответ 12,5.

3.            а) Периметр ромба равен 24, а один из углов равен 30°. Найдите площадь ромба.

Ответ 18.

б) Периметр ромба равен 36, а один из углов равен 30°.

Найдите площадь ромба.

Ответ 40,5.

в) Периметр ромба равен 56, а один из углов равен 30°. Найдите площадь ромба.

Ответ 98.

4.            а) Найдите площадь ромба, если его диагонали равны 12 и 7.

Ответ 42.

б) Найдите площадь ромба, если его диагонали равны 18 и 9.

Ответ 81.

в) Найдите площадь ромба, если его диагонали равны 5 и 11.

Ответ 27,5.

5.                  а)   Найдите   площадь   квадрата,   описанного   вокруг окружности радиуса 3.

Ответ 36.

б) Найдите площадь квадрата, описанного вокруг окружности радиуса 7.

Ответ 196.

в) Найдите площадь квадрата, описанного вокруг окружности радиуса 8.

Ответ 256.

6.             а) Площадь ромба равна 60, а периметр равен 40. Найдите высоту ромба.

Ответ 6.

б) Площадь ромба равна 72, а периметр равен 72. Найдите высоту ромба.

Ответ 4.

в) Площадь ромба равна 54, а периметр равен 36. Найдите высоту ромба.

Ответ 6.

7. 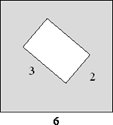    а) Из квадрата со стороной 6 вырезали прямоугольник. Найдите площадь получившейся фигуры, если стороны прямоугольника равны 2 и 3.

Ответ 30.

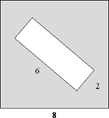б) Из квадрата со стороной 8 вырезали прямоугольник. Найдите площадь получившейся фигуры, если стороны прямоугольника равны 6 и 2

Ответ 52.

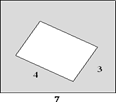в) Из квадрата со стороной 7 вырезали прямоугольник. Найдите площадь получившейся фигуры, если стороны прямоугольника равны 4 и 3.

Ответ 37.

Задачи с развернутым ответом.

1.           

Ответ 36√3.

2.           

Ответ: 27√3.

Пример решения задачи с развернутым ответом

1. Прямая, проходящая через вершину В прямоугольника АВСD перпендикулярно диагонали АС, пересекает сторону АD в точке М, равноудаленной от вершин В и D. Найдите площадь прямоугольника АВСD, если ВС = 6√3.

Решение.

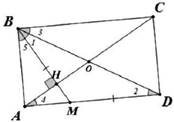Треугольник ВМD – равнобедренный, так как ВМ

=МD по условию. Тогда в треугольнике ВМ D углы 1 и 2 равны. Углы 2 и 3 равны как накрест лежащие углы при параллельных прямых ВС и АD и секущей ВD.

Треугольник АОD – равнобедренный, так как АО

=ОD (ВD = АС по свойству диагоналей прямоугольника: АО = ОС = BО = ОD), тогда углы 4 и 2 равны.

Прямоугольные треугольники АВС и ВDА равны по катету и гипотенузе (АВ- общий катет, ВD = АС – гипотенузы). Тогда ∠ВСА = ∠ВDА.

Н – точка пересечения отрезков ВМ и АС, где ВМ⊥АС по условию.

Треугольник АВМ – прямоугольный, АН- высота, тогда из подобия прямоугольных треугольников углы 5 и 4 равны.

∠ 5= ∠ 1= ∠ 3= 90:3 =30⁰.

В прямоугольном треугольнике ВАС: АВ = ВС∙ tg 30⁰. 6

S_ABCD = AB ∙ BC = 6 ∙ 6√3. = 36√3.

Ответ: 36√3.

Решение задания 2 аналогичное.