3.26 Вписанные углы

Вписанные углы.

Повторяем теорию.

Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность.

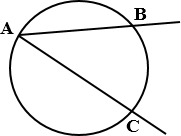Точки А, В, С лежат на окружности, следовательно.

∠ВАС – вписанный угол, опирающийся на дугу ВС.

Свойства

1.     Вписанный угол равен половине угловой величины дуги, на которую он опирается.

∠ ВАС = ¹ È ВС.

2

2. 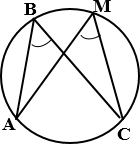    Вписанные углы, опирающиеся на одну и ту же дугу, равны.

Точки А, В, М, С лежат на окружности, причем В, M лежат по одну сторону от прямой АС,

∠АВС = ∠АМС.

3. 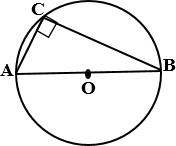    Вписанный       угол,       опирающийся на полуокружность (на диаметр), равен 90^О.

4. 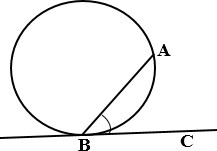    Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними.

ВА – хорда, ВС – касательная, следовательно,

∠ АВС = ¹ È АВ

2

5. 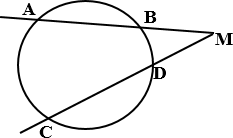    (дополнительно) Угол между двумя секущими, пересекающимися вне круга, равен полуразности дуг, высекаемых секущими на окружности.

∠М = È𝐴𝐶−È𝐵𝐷

2

6. 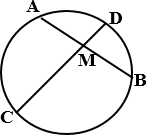    (дополнительно) Угол между пересекающимися хордами равен полусумме противоположных дуг, высекаемых хордами.

АВ и СD – хорды,

∠𝐴𝑀𝐷 = ÈAD+ÈCB

2

Проверяем себя

Т1. Вставьте пропущенные слова:

а) Угол АВС является вписанным, если точка В           , а лучи ВА и ВС            . б) Вписанные углы равны, если они                      на одну                .

в) Угол АОВ является центральным, если точка О является              , а лучи ОА

и ОВ              .

г) Вписанный угол, опирающийся на диаметр, …

Ответ: а) лежит на окружности, пересекают окружность; б) опираются, дугу; в) центром окружности, пересекают окружность, г) является прямым.

Т2. Выберите верное утверждение:

а) Прямая, проходящая через две точки окружности, называется диаметром. б) Прямая, имеющая с окружностью только одну общую точку, называется

касательной к окружности.

в) Центр окружности – это середина окружности.

г) Угол, вершина которого лежит на окружности называется вписанным углом.

Ответ: б)

Т3. Какие углы на рисунках называются вписанными?

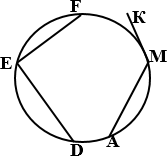Ответ: ∠𝐹𝐸𝐷, ∠𝐾

Решаем задачи

1. 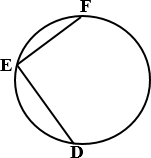              а) Найдите ∠DEF, если градусные меры дуг DE и

EF равны 150° и 68° соответственно.

Ответ: 71

б) Найдите ∠DEF, если градусные меры дуг DE и

EF равны 75° и 13° соответственно.

Ответ: 136

в) Найдите ∠DEF, если градусные меры дуг DE и

EF равны 47° и 203° соответственно.

Ответ: 55

2. 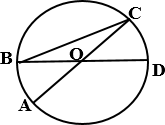           а) Величина центрального угла AOD равна 110°. Найдите величину вписанного угла ACB. Ответ дайте в градусах.

Ответ: 35

б) Величина центрального угла AOD равна 70°. Найдите величину вписанного угла ACB. Ответ дайте в градусах

Ответ: 55

в) Величина центрального угла AOD равна 140°. Найдите величину вписанного ACB. Ответ дайте в градусах.

Ответ: 20

3. 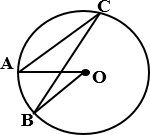           а) Точка О — центр окружности, ∠AOB = 84° (см. рисунок). Найдите величину угла ACB (в градусах).

Ответ: 42

б) Точка О — центр окружности, ∠AOB = 106° (см. рисунок). Найдите величину угла ACB (в градусах).

Ответ: 53

в) Точка О — центр окружности, ∠AOB = 77° (см. рисунок). Найдите величину угла ACB (в градусах).

Ответ: 38,5

4. 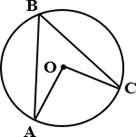           а) Точка О – центр окружности, на которой лежат точки А, В и С. Известно, что ∠АВС = 61° и ∠ОАВ = 8°. Найдите угол ВСО. Ответ дайте в градусах.

Ответ: 53

б) Точка О – центр окружности, на которой лежат точки А, В и С. Известно, что ∠АВС = 103° и ∠ОАВ = 24°. Найдите угол ВСО. Ответ дайте в градусах.

Ответ: 79

в) Точка О – центр окружности, на которой лежат точки А, В и С. Известно, что ∠АВС = 47^О и ∠ОАВ = 22^О. Найдите угол ВСО. Ответ дайте в градусах.

Ответ: 25

5. 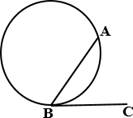              а) На окружности отмечены точки A и B так, что меньшая дуга AB равна 92°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Ответ: 46

б)   На   окружности   отмечены   точки A и B так,       что меньшая                             дуга AB равна 134°.              Прямая BC касается

окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Ответ: 67.

в) На окружности отмечены точки A и B так, что меньшая дуга AB равна 66°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Ответ: 33.

6. 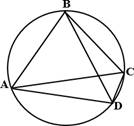           а) Точки A, B, C, D последовательно расположены на окружности. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.

Ответ: 21

б) Точки A, B, C, D последовательно расположены на окружности. Угол ABC равен 105°, угол АВD равен 37°. Найдите угол САD. Ответ дайте в градусах.

Ответ: 68

в) Точки A, B, C, D последовательно расположены на окружности. Угол ABC равен 91°, угол CAD равен 27°. Найдите угол ABD. Ответ дайте в градусах.

Ответ: 64

7.       а)  Вершины  равнобедренного треугольника ABC, в котором AB = BC и

∠ABC = 177°, лежат на окружности с центром в точке O. Найдите величину угла BOC. Ответ дайте в градусах.

Ответ: 3

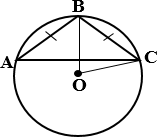б) Вершины равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 80°, лежат на окружности с центром в точке O. Найдите величину угла BOC. Ответ дайте в градусах.

Ответ: 100

в) Вершины равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 103°, лежат на окружности с центром в точке O. Найдите величину угла BOC. Ответ дайте в градусах.

Ответ: 77

Задачи с развернутым ответом.

a.      Расстояния от одного конца диаметра до концов параллельной ему хорды равны 13 и 84. Найдите радиус окружности.

Ответ: 42,5

b.     Из одной точки к окружности проведены две секущие. Дуги, высекаемые секущими на окружности, равны 46° и 94°. Найдите угол между секущими.

Ответ: 24