3.28 Площадь треугольника

Площадь треугольника Повторяем теорию.

Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки называют сторонами треугольника, а точки – вершинами треугольника Площадь треугольника – это численная характеристика, характеризующая размер плоскости, ограниченной треугольником.

Вспомним обозначения и рассмотрим чертеж:

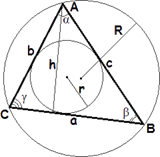S - площадь треугольника, a, b, c - длины сторон треугольника,

h -     высота     треугольника,    γ -     угол     между сторонами a и b,

r - радиус вписанной окружности, R - радиус описанной окружности.

Полупериметр треугольника 𝑝 = 𝑎+𝑏+𝑐

2

1. Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.

1

𝑆 =

𝑎ℎ

2

2. Формула площади треугольника по трем сторонам

Формула Герона 𝑆 = √𝑝(𝑝 − 𝑎)(𝑝 − 𝑏)(𝑝 − 𝑐)

3. Формула площади треугольника по двум сторонам и углу между ними. Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

1

𝑆 = 2 𝑎 ∙ 𝑏 ∙ sin 𝛾

4. Формула площади треугольника по трем сторонам и радиусу описанной окружности.

Площадь треугольника равна отношению произведения всех сторон треугольника к 4 радиусам описанной окружности

𝑎𝑏𝑐

𝑆 =

4𝑅

5. Формула площади треугольника по трем сторонам и радиусу вписанной окружности. Площадь треугольника равна произведению полупериметра треугольника на радиус вписанной окружности.

𝑆 = 𝑝 ∙ 𝑟

6. 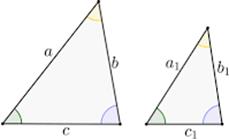Свойство подобных треугольников.

Отношение          площадей          подобных треугольников равно квадрату коэффициента подобия.

𝑆1

𝑆2

= 𝑘²

, где

𝑎

𝑎1

𝑏

=

𝑏1

𝑐

=

𝑐1

= 𝑘

7. 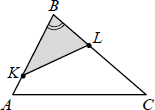Свойства площадей треугольников с равными углами.

Если два треугольника имеют равные углы, то их площади относятся как произведения сторон, заключающих эти углы.

𝑆1

𝑆2

= 𝐵𝐾∙𝐵𝐿

𝐴𝐵∙𝐵𝐶

8. 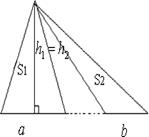  Свойства площадей треугольников с равными высотами.

Если два треугольника имеют одинаковые высоты, то их площади относятся как длины оснований (сторон, на которые опущены эти высоты).

𝑆1

𝑆2

𝑎

= 𝑏

9. 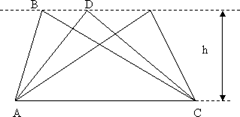Еще одно интересное свойство площадей Если вершину треугольника передвигать по

прямой, параллельной основанию, то площадь при этом не изменится.

S₁=S₂=…S_n=hˑAC=const

Треугольники   называются   равновеликими,   если    имеют    одинаковую площадь.

10. 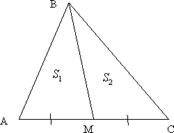            Свойство медианы треугольника

Медиана треугольника разбивает его на два равновеликих треугольника.

Если ВМ-медиана, то S₁=S₂

11. 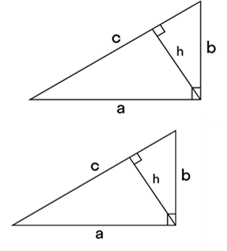  Площадь прямоугольного треугольника равна половине произведения его катетов.

𝑆 = 𝑎𝑏

             2

12. Площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту, проведенную к ней.

𝑆 = 𝑐ℎ

            2

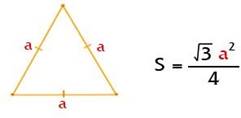
13. Площадь равностороннего треугольника равна

Проверяем себя.

Т1. Какое из следующих утверждений верно?

1)  В параллелограмме есть два равных угла.

2)     Каждая из биссектрис равнобедренного треугольника является    его медианой.

3)    Площадь прямоугольного треугольника равна произведению длин его катетов.

Ответ: 1

Т2. Какие из следующих утверждений верны?

1)           Отрезки касательных, проведенные к окружности из одной точки, равны.

2)           Длина любой хорды окружности не больше её радиуса.

3)           Площадь треугольника равна произведению основания и проведенной к нему высоты.

Ответ: 1

Т3. Выберите верное утверждение:

1)  Площадь параллелограмма равна произведению его диагоналей.

2)  Медиана делит треугольник на два равновеликих треугольника.

3)         Отношение   площадей   подобных   треугольников   равно   квадрату коэффициента подобия.

Ответ: 23

Решаем задачи.

1. 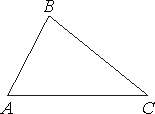    а) В треугольнике ABC известно, что AB=6,

BC=10,

sinÐABC = 1 .                  Найдите        площадь

3

треугольника ABC.

Ответ:10.

б) В треугольнике ABC известно, что AB=14, BC=5,

sinÐABC = 6 . Найдите площадь треугольника ABC.

7

Ответ:30.

в) В треугольнике ABC известно, что AB=16, BC=25, sinÐABC = 3 .

10

Найдите площадь треугольника ABC.

Ответ: 60.

2. 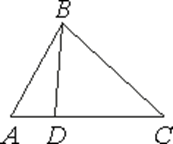    а) На стороне AC треугольника ABC отмечена точка D так,              что AD=6, DC=10.                Площадь треугольника ABC равна 48. Найдите площадь треугольника ABD.

Ответ: 18.

б)   На   стороне AC треугольника ABC   отмечена точка D так,                           что AD=4, DC=7.                 Площадь

треугольника ABC равна 55. Найдите площадь треугольника ABD.

Ответ: 20.

в)   На   стороне    AC    треугольника    ABC    отмечена    точка    D    так, то AD=2, DC=13. Площадь треугольника ABC равна 75. Найдите площадь треугольника ABD.

Ответ: 10.

3. 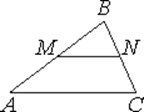                      а) Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=21, MN=14. Площадь треугольника ABC равна 27. Найдите площадь треугольника MBN.

Ответ: 12.

б) Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и ВC в точках M и N соответственно, AC=27, MN=18. Площадь треугольника ABC равна 63. Найдите площадь треугольника MBN.

Ответ: 28.

в) Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=36, MN=27. Площадь треугольника ABC равна 96. Найдите площадь треугольника MBN.

Ответ: 54.

4.           а). треугольника

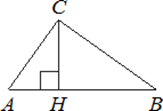
На    гипотенузу    AB    прямоугольного ABC опущена высота CH, AH=2, BH=18.

Найдите площадь треугольника.

Ответ: 60.

б). На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=4, BH=16. Найдите площадь треугольника.

Ответ: 80.

в). На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=7, BH=28. Найдите площадь треугольника.

Ответ: 245.

5.     а) Катеты прямоугольного треугольника равны 10 и 24. Найдите площадь треугольника.

Ответ: 120.

б) Катеты прямоугольного треугольника равны 20 и 15. Найдите площадь треугольника.

Ответ: 150.

в) Катеты прямоугольного треугольника равны 12 и 5. Найдите площадь треугольника.

Ответ: 30.

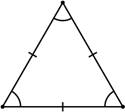
6.     а)        Сторона     равностороннего треугольника равна 14√3. Найдите площадь треугольника, деленную на √3.

б) Сторона равностороннего треугольника равна 12√3

. Найдите площадь треугольника, деленную на √3.

Ответ: 108.

в) Сторона равностороннего треугольника равна 10√3 . Найдите площадь треугольника, деленную на √3.

Ответ: 75.

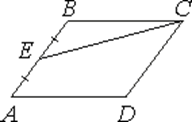
7.            а) Площадь параллелограмма ABCD равна 68. Точка E                    — середина стороны      AB. Найдите площадь треугольника CBE. Ответ: 17.

б) Площадь параллелограмма ABCD равна 84. Точка E — середина стороны AB. Найдите площадь треугольника CBE.

Ответ: 21.

в) Площадь параллелограмма ABCD равна 148. Точка E — середина стороны AB. Найдите площадь треугольника CBE.

Ответ: 37.

Задачи с развернутым ответом

1.      Катеты прямоугольного треугольника равны 15 и 36. Найдите высоту, проведенную к гипотенузе.

Ответ: ¹⁸⁰

                       13

2.            Внутри параллелограмма ABCD выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади параллелограмма.