3.29 Площадь круга и его частей.

Площадь круга и его частей.

Повторяем теорию

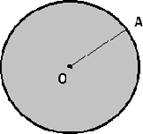
Круг — это часть плоскости, ограниченная окружностью.

Центр данной окружности называется центром круга, а расстояние от центра до любой точки окружности — радиусом круга.

O — центр круга, OA — радиус круга.

Длина окружности — это длина замкнутой плоской кривой, ограничивающей круг.

𝐶 = 2𝜋𝑟.

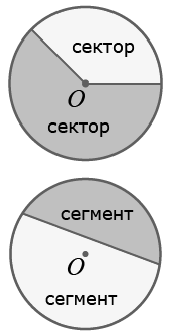Круговой сектор — это часть круга, ограниченная двумя радиусами и дугой. Два радиуса разделяют круг на два сектора.

Круговой сегмент — это часть круга, ограниченная дугой и стягивающей её хордой. Любая хорда делит круг на два сегмента.

Площадь круга

Площадь круга равна произведению числа π на квадрат радиуса.

𝑆 = 𝜋𝑟², где S — площадь круга, а r — радиус круга.

Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2. Следовательно, формула нахождения площади

круга через диаметр будет выглядеть так:

Площадь сектора.

pd 2

S              .

4

Чтобы найти площадь S кругового сектора радиуса R, ограниченного дугой с градусной мерой n°, надо использовать формулу:

pr2

S =        × n

360

Площадь сегмента.

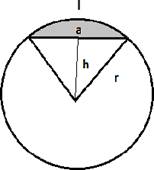При    отсечении части     круга       хордой    можно рассмотреть две фигуры: это сегмент и равнобедренный треугольник, боковые стороны которого - радиусы круга. Площадь   сегмента   можно   найти   как   разность площадей   сектора   круга   и   этого   равнобедренного

треугольника.

S = 1 (rl - ah)

2

Проверяем себя.

Т1. Вставьте пропущенное слово:

а) Круг — это часть плоскости, ограниченная                             .

б) Сектор — это часть круга, ограниченная двумя радиусами и          .

в) Площадь круга равна произведению числа π на квадрат             .

г) Площадь сегмента можно найти как разность площадей           круга и равнобедренного треугольника.

Ответ: а) окружностью; б) дугой; в) радиуса; г) сектора.

Т2. Выберите верное утверждение Круговым сегментом называется…

1)           Часть круга, ограниченная дугой окружности и хордой, соединяющей концы этой дуги.

2)           Часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

3)           Часть плоскости, ограниченная окружностью. Ответ: 1.

Т3. Выберите верное утверждение Чтобы найти площадь круга нужно:

1)  число π умножить на радиус.

2)  число π  умножить на квадрат диаметра и разделить на четыре.

3)  число π разделить на квадрат диаметра.

Ответ: 2.

Решаем задачи.

2.     а) Найдите площадь круга, если радиус равен 5. (𝜋 ≈ 3).

Ответ: 75.

б) Найдите площадь круга, если радиус равен 8. (𝜋 ≈ 3).

Ответ: 192.

в) Найдите площадь круга, если радиус равен 12. (𝜋 ≈ 3).

Ответ: 432.

3.                  а) Найдите площадь кругового сектора, если радиус круга равен 3, а угол сектора равен 120°. В ответе укажите площадь, деленную на π.

Ответ: 3.

б) Найдите площадь кругового сектора, если радиус круга равен 4, а угол сектора равен 90⁰. В ответе укажите площадь, деленную на π.

Ответ: 4.

в) Найдите площадь кругового сектора, если радиус круга равен 3,6, а угол сектора равен 300⁰. В ответе укажите площадь, деленную на π.

Ответ: 10,8.

его

4.             а) Найдите площадь кругового сектора, если длина ограничивающей дуги равна 6π, а угол сектора равен 120°. В ответе укажите площадь,

деленную на π. Ответ: 27.

б) Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 3π, а угол сектора равен 240⁰ . В ответе укажите площадь, деленную на π.

Ответ: 3.375

в) Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 5π, а угол сектора равен 36⁰ . В ответе укажите площадь, деленную на π.

Ответ: 62,5.

5.                 5а) Площадь   сектора   составляет   3/8   площади   круга.   Найдите центральный угол, соответствующий данному сектору.

Ответ:135.

б)   Площадь   сектора   составляет   9/20   площади   круга.   Найдите центральный угол, соответствующий данному сектору.

Ответ: 162.

в) Площадь сектора составляет 8/15 площади круга. Найдите центральный угол, соответствующий данному сектору.

Ответ: 192.

6.            а) Найдите площадь кругового сегмента, если радиус круга равен 10, а градусная мера дуги сегмента равна 150⁰. (𝜋 ≈ 3).

Ответ: 100.

б) Найдите площадь кругового сегмента, если радиус круга равен 4, а градусная мера дуги сегмента равна 150⁰. (𝜋 ≈ 3).

Ответ: 16.

в) Найдите площадь кругового сегмента, если радиус круга равен 6, а градусная мера дуги сегмента равна 150⁰. (𝜋 ≈ 3).

Ответ: 36.

7.              а) Найдите радиус круга, если площадь сектора этого круга равна 7,5𝜋, а

центральный угол, соответствующий этому сектору, равен 108⁰.

Ответ: 5.

б) Найдите радиус круга, если площадь сектора этого круга равна 45𝜋, а центральный угол, соответствующий этому сектору, равен 72⁰.

Ответ: 15.

в) Найдите радиус круга, если площадь сектора этого круга равна 60𝜋, а центральный угол, соответствующий этому сектору, равен 54⁰.

Ответ: 20.

Задачи с развернутым ответом.

1.            Найдите площадь круга, вписанного в сектор круга радиуса 20 см с хордой 10 см.

Ответ: 16 𝜋 см².

2.            Радиус круга равен 2см. По разные стороны от центра круга проведены две параллельные хорды, равные соответственно сторонам правильного треугольника и правильного шестиугольника, вписанных в данный круг. Найдите площадь части круга, находящегося между хордами.

Ответ: 2p + 2      .