3.29 Вписанная в треугольник окружность

Вписанная в треугольник окружность.

Повторяем теорию.

В этом случае треугольник называется описанным около окружности.

Свойства

1. 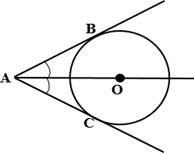     Центр вписанной в угол окружности лежит на биссектрисе угла.

Окружность с центром О вписана в угол ВАС, следовательно. ∠ВАО = ∠САО.

2.      В любой треугольник можно вписать окружность и притом только одну.

3. 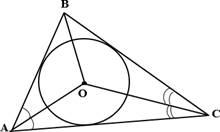    Центром     вписанной     окружности     треугольника     является точка пересечения его биссектрис.

В △ АВС О    –   центр   вписанной                       окружности, следовательно, ВО, СО, АО – биссектрисы углов

△ АВС.

4. 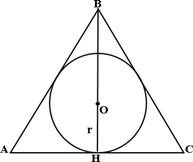    Радиус           вписанной           окружности равностороннего   треугольника   равен одной трети  его    биссектрисы (она           же является медианой               и   высотой    равностороннего треугольника).

△ АВС – равносторонний,

BH– биссектриса, высота, медиана O – центр вписанной окружности,

r– радиус вписанной окружности, 𝑟 = 1

3

𝐵𝐻

Если сторона треугольника равна а, то   𝒓 =     𝒂 .

𝟐√𝟑

5.     Площадь S треугольника равна произведению полупериметра p этого треугольника на радиус r вписанной окружности этого треугольника:

𝑆 = 𝑝𝑟

6. 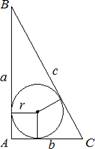     Если треугольник прямоугольный, то

𝒓 = 𝒂+𝒃−𝒄 .

𝟐

Проверяем себя.

Т1. Вписанная в треугольник окружность изображена на рисунке:

Ответ: в)

Т2. Какие из данных утверждений верны?

а) В любой треугольник можно вписать окружность.

б)    Центром   вписанной   в    треугольник   окружности   является       точка пересечения его биссектрис.

в) Площадь круга больше квадрата длины его диаметра.

г) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.

д) Из двух хорд окружности больше та, середина которой находится дальше от центра окружности.

е) Для точки, лежащей внутри круга, расстояние до центра круга меньше его радиуса.

Ответ: а), б), г), е)

Т3. Выберите верное утверждение:

1)    Центр   вписанной   в    треугольник   окружности   совпадает   с точкой пересечения его…

а) Медиан.

б) Биссектрис.

в) Серединных перпендикуляров.

2)    Центр вписанной в треугольник окружности равноудален от… а) Сторон.

б) Углов.

в) Вершин треугольника.

3)    Если   центр   вписанной   в   треугольник   окружности   является точкой пересечения его медиан, то этот треугольник:

а) Прямоугольный. б) Равнобедренный. в) Равносторонний.

4)    Окружность называется вписанной в треугольник, если… а) Все его стороны касаются окружности.

б) Все его вершины лежат на окружности.

в) Все его стороны имеют общие точки с окружностью.

5)    Радиус вписанной в треугольник окружности равен расстоянию от центра окружности до…

а) Сторон треугольника. б) Вершин треугольника. в) Углов треугольника.

6)    Центр   вписанной  в   равнобедренный   треугольник  окружности может лежать…

а) На любой из его высот. б) На одной из его медиан.

в) На любом из его серединных перпендикуляров.

7)    Если   центр   вписанной   в   треугольник   окружности   является точкой пересечения его биссектрис, то этот треугольник может быть…

а) Произвольным.

б) Только равносторонним. в) Только прямоугольным.

Ответ: 1.б); 2.а); 3.в); 4.а); 5.а); 6.б); 7.а)

Решаем задачи

1. 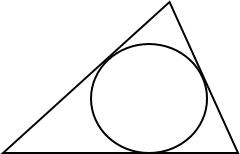  а) Периметр треугольника равен 48, одна из сторон равна 18, а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.

Ответ: 72

б) Периметр треугольника равен 71, одна из сторон равна 21, а радиус вписанной в

него окружности равен 6. Найдите площадь этого треугольника.

Ответ: 213

в) Периметр треугольника равен 56, одна из сторон равна 19, а радиус вписанной в него окружности равен 5. Найдите площадь этого треугольника.

Ответ: 140

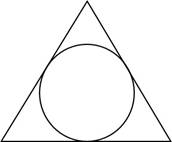
2.                   а) Сторона равностороннего треугольника равна 2 √3 . Найдите радиус окружности, вписанной в этот треугольник.

Ответ: 1

б) Сторона равностороннего треугольника равна 6 √3 . Найдите радиус окружности, вписанной в этот треугольник.

Ответ: 3

в) Сторона равностороннего треугольника равна 4 √3 . Найдите радиус окружности, вписанной в этот треугольник.

Ответ: 2

3. 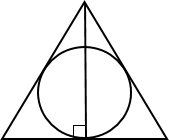                 а) Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника.

Ответ: 15

б) Радиус окружности, вписанной в равносторонний треугольник, равен 7. Найдите высоту этого треугольника.

Ответ: 21

в) Радиус окружности, вписанной в равносторонний треугольник, равен 8. Найдите высоту этого треугольника.

Ответ: 24

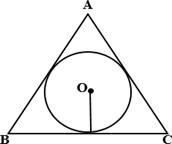
4.                  а) Радиус окружности, вписанной в равносторонний треугольник, равен 2√3 . Найдите длину стороны этого треугольника.

Ответ: 12

б) Радиус окружности, вписанной в равносторонний треугольник, равен 4√3 . Найдите длину стороны этого треугольника.

Ответ: 24

6√3. Найдите длину стороны этого треугольника.

Ответ: 36

5. 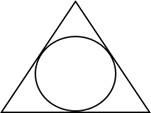              а) Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 132.

Ответ: 44

б)    Найдите   радиус   окружности,   вписанной   в правильный треугольник, высота которого равна 96.

Ответ: 32

в) Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 15.

Ответ: 5

6.            (При решении данной задачи можно использовать как готовую формулу 6, так и другой способ.)

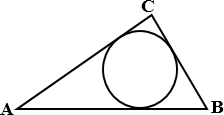а) В треугольнике АВС АС = 4, ВС = 3, угол С равен 90°. Найдите радиус вписанной окружности.

Ответ: 1.

б) В треугольнике АВС АС = 12, ВС = 5, угол С равен 90°. Найдите радиус вписанной окружности.

Ответ: 2

в) В треугольнике АВС АС = 8, ВС = 6, угол С равен 90°. Найдите радиус вписанной окружности.

Ответ: 2

7. 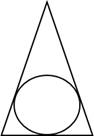         а) Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

Ответ: 22

б) Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два

отрезка,    длины    которых    равны    15    и    4,    считая    от                 вершины, противолежащей основанию. Найдите периметр треугольника.

Ответ: 46

в) Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 12 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

Ответ: 28.

Задачи с развернутым ответом.

a.      Найдите периметр прямоугольного треугольника, если радиус вписанной окружности 2 см, а гипотенуза 13 см.

Ответ: 30 см.