33. Сравнение рациональных чисел. Методические к уроку

Методические рекомендации к уроку

Тема урока "Сравнение рациональных чисел "

Цели обучения:

6.1.2.8

сравнивать целые числа;

6.1.2.12

сравнивать рациональные числа.

Критерии оценивания

Учащийся

знает:

·                    понятие целого числа;

·                    понятие рационального числа;

умеет:

·                    использовать целые числа при описании величин;

·                    изображать рациональные числа на координатной прямой;

•                     сравнивать целые числа;

•                     сравнивать рациональные числа.

•                     применять  при решении задач.

Теоретический материал:

Сравнение рациональных чисел

Сравнить два рациональных числа – значит узнать какое из них больше, какое меньше, или определить, что числа равны. Любое положительное число больше нуля и больше любого отрицательного числа.

Примеры: 1 > 0;    15 > -16;    0,001 > -100

Любое отрицательное число меньше нуля и меньше любого положительного числа.

Примеры: -7 < 0;    -1,25 < 0,05    -357 < 0

            Из двух отрицательных чисел больше то, у которого модуль меньше

Примеры: -31 < -28;    -0,5 > -0,51

            Два рациональных числа равны, если равны их модули и они имеют одинаковый знак.

Примеры: -31 = -31;    0 = 0;    7 = 7

Ход урока

Организационный момент. Актуализация опорных знаний.

- Концентрация внимания учащихся: устный опрос.

1.                  Какое число больше: положительное или отрицательное?

2.                  Какое из двух отрицательных чисел считают большим, чем другое? А какое из них – меньшим?

3.                  Какое из чисел больше: отрицательное или 0?

4.                  Какое из чисел меньше: положительное или 0?

5.                  Как расположены на координатной прямой точки A(a) и B(b), если a меньше b?

- Совместно с учащимися определить цели урока/ЦО;

- Определить «зону ближайшего развития» учащихся, ожидания к концу урока.

- Проверка домашнего задания.

- Определить тему урока.

Индивидуальная работа. Раздать каждому задание: Приложение 1. Выполнять надо самостоятельно.

Приложение 1

Задание 1:

1.   Какое значение температуры больше, а какое меньше? Запиши ответ, используя знак :

а) 5;                б) -3;                 в) 2 ;                    г) -10

2.      Отметьте схематически на координатной прямой числа: 2,4; -5; ; -1; -3,8; -10,5. Сравни их с нулем. Сделайте вывод.

Задание 2:

Заполни пропуски.

1)      Если модуль числа больше самого числа, то оно ... (отрицательное).

2)      Если модуль равен самому числу, то данное число равно ... (0 или положительное).

3)      На координатной прямой между числами -4,5 и -2 лежат ...  целых числа. (2)

Задание 3:

Ответь "Да" если верно, "Нет" - если не верно.

4)      Из двух чисел с разными знаками больше то, у которого модуль больше. (Нет)

5)      -4,6 > - 4,5. (Нет)

6)      Если х>0, то -х<0. (Да)

7)      Точка с меньшей координатой лежит на координатной прямой левее точки с большей координатой. (Да)

8)      Большее из двух положительных чисел имеет больший модуль. (Да)

9)      Любое отрицательное число меньше положительного. (Да)

10)  Нуль больше любого положительного числа. (Нет)

Проверить ответы по ключам. Оценить процентное отношение правильно выполнивших задание к числу опрошенных.

Коллективная с классом. Повторить выводы прошлого урока:

Расположение точек на числовой оси позволяет наглядно сравнивать между собой числа.

Напомним, что если координатная прямая изображена горизонтально, то положительные числа изображаются точками правее 0, а отрицательные — левее 0. В этом случае, если положительные числа отметить точками на этой прямой, то большему из двух чисел будет соответствовать точка, расположенная на числовой оси правее, а меньшему — точка, расположенная на координатной прямой левее.

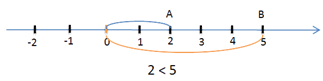
Из двух чисел на координатной прямой больше то, которое расположено правее, а меньше то, которое расположено левее.
Это означает, что при сравнении рациональных чисел:

·                     любое положительное число больше нуля и больше любого отрицательного числа;

·                     любое отрицательное число меньше нуля и меньше любого положительного числа.

Пример.

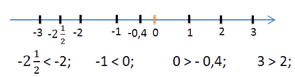
Решаются задания из учебного пособия "Математика 6" или из Приложения 2.

Приложение 2

Ответы и решения.

Сверив ответы по ключам, предложить сравнить: сначала задания, затем ответы и предложить сделать выводы на основании своих сравнений. Использовать прием "Активный класс". Пригласить к доске двух учеников и попросить их записать свои решения. Затем свой вывод. Ученики на местах пишут свои выводы и сверяют с записями на доске. С целью развития математической речи попросите нескольких учеников прокомментировать этапы своих размышлений.

Вывод:

1)                 Из двух положительных чисел больше то, чей модуль больше.

При сравнении двух отрицательных чисел большее будет расположено правее, то есть ближе к началу отсчёта. Значит, его модуль (длина отрезка от нуля до числа) будет меньше.

2)                 Из двух отрицательных чисел больше то, модуль которого меньше.

Привести еще пример рассуждений при решении аналогичных заданий.

Следующее задание для отработки навыков математической речи.

Задание. Сравнить числа «−6» и «−12.

Решение: Точка, соответствующая числу «−6» расположена ближе к началу отсчёта и правее, чем точка, соответствующая числу «−12».

«|−6| < |−12|», значит, «−6 > −12».

Ноль больше любого отрицательного числа, но меньше любого положительного числа.

В диалоге с учащимися ввести Правила сравнения отрицательных чисел

На числовой прямой меньшее отрицательное число располагается левее большего отрицательного числа, - при выводе правил делаем проверку с помощью координатной прямой.

Сравнение отрицательных чисел

Сравнение отрицательных чисел основывается на сравнении модулей этих чисел.

Пример: Сравнить отрицательные числа −27 и −4.

Решение. Согласно правилу сравнения отрицательных чисел найдем сначала модули чисел –27 и –4, а затем сравним полученные положительные числа.

|−27|=27; |−4|=4

Сравним полученные натуральные числа: 27>4.

Таким образом, получаем, что –27<−4.

Ответ:–27

Выводим правила: Правило сравнения отрицательных чисел:

1) Если модуль одного из отрицательных чисел больше, то такое число является меньшим;

2) если модуль одного из отрицательных чисел меньше, то такое число является большим; 

3) если модули чисел равны, то отрицательные числа равны.

Правило сравнения чисел с противоположными знаками.

Пример: Сравнить целые числа −53 и 8.

Решение. Числа имеют противоположные знаки. Согласно правилу сравнения чисел с противоположными знаками получаем, что отрицательное число −53 меньше положительного числа 8.

Ответ: −53.

Вывод правила: Положительное число всегда больше отрицательного, а отрицательное число всегда меньше положительного.

Если числа заданы как числовые выражения, то сразу невозможно определить какие они имеют знаки. В таком случае нужно вычислить значение этих выражений и затем определить, какое из правил сравнения можно применить.

Групповая работа. Объединить учащихся в разноуровневые группы по 4 - 6 учеников. Раздать каждой группе задания.

Приложение 3.

1)      Сравни с нулем числа: -4,36; 0,01; -7; -; 2,05; -0,058.

2)      Сравни числа. Что общего и что различного в примерах каждого столбика? Сделайте вывод.

а) -2 и 5;                                                             д) -1 и -7;

б) 3 и -3,4;                                                          е) -2,8 и -4;

в) -;                                                         ж) - ;

г) 5,12 и -5,72;                                                   з) -19,2 и -8,9

3)      Сравни числа:

а) 2 и 4,5;                        д) -;                                и) -2;

б) -1,8 и -1,6;                  е) 2,6 и -6,2;                              к) -0,806 и -7,5

в) -95,3 и 0,24;               ж) -;                               л) -;

г) -59,9 и -60;                  з) -0,2 и -0,03;                          м) -4,009 и -4,01

5. Расположи числа в порядке возрастания, сопоставь им соответствующие буквы и расшифруй слова. Что они означают?

1)8,5;     -2,19;          -2,9;        -15;     -9;    -16,4;        3;       -9,2

   Я             Ц               Е            Р          А         Т            И        П

2) -7,8;      60;           0;          -52;            -0,4;         -39,6;       7,2;        5,6;         -18;        -21,5

      Н          О             С            К                  О              Р             Ь            Т             Ж              У

Учитель проходит по рядам, слушает, при необходимости корректирует рассуждения, решения учащихся, проверяет и оценивает похвалой работу групп.

Проверяет результаты работы групп и совместно разбирает возможные ошибки.

Предоставить учащимся достаточно времени для выполнения заданий.

Старший группы оценивает вклад каждого, выставляя отметку.

Рефлексия. Учащимся предлагается оценить свои знания по теме:

Лесенка достижений:

•      Сегодня на уроке я научился…

•      Мне было интересно..

•      Мне было трудно…

•      Я понял, что…

•      Я почувствовал, что…

•      Больше всего мне понравилось…

•      Своей работой на уроке я доволен (не совсем, не доволен), потому что…

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости). Ученики, распределяя в паре задания, самостоятельно выбирают уровень сложности.

Предусмотрена самопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить модули, сравнивать числа, проводить проверку с помощью координатной прямой, начертив схематично и выбрав начало отсчета отмечать точки с учетом расположения в зависимости от координат. При сравнивании чисел умение анализировать практические примеры и делать теоретические выводы.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

"Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

"Математика 6", Алдамуратова Т.А, Байшоланов Т.С.;

Самостоятельные и контрольные работы, Ершова А.П., Голобородько В.В.