3.30 Описанная около треугольника окружность

Описанная около треугольника окружность.

Повторяем теорию.

Окружность называется описанной около треугольника, если все вершины треугольника лежат на окружности.

В этом случае треугольник называется вписанным в окружность.

Свойства.

а) Около любого треугольника можно описать окружность и притом только одну.

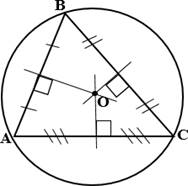
б) Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к его сторонам.

△ АВС, О – центр описанной окружности

в) Радиус              описанной                    окружности равностороннего треугольника равен двум третям его высоты (она же является медианой и  биссектрисой              равностороннего треугольника).

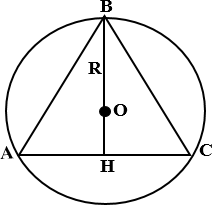
△ АВС – равносторонний,

ВН – биссектриса, высота, медиана,

О – центр описанной окружности,

𝑅 – радиус вписанной окружности

2

𝑅 =

𝐵𝐻

3

г) Центром описанной окружности прямоугольного треугольника является середина его гипотенузы, а радиус окружности равен половине гипотенузы.

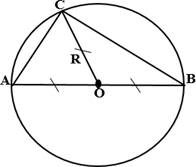
△ АВС – прямоугольный,

∠С – прямой,

О – центр описанной окружности,

𝑅 – радиус вписанной окружности

1

𝑅 = 2 АВ

д) Площадь Sтреугольника может быть найдена по формуле 𝑆 =

𝑎𝑏𝑐

4𝑅

, где a,

b, c – длины сторон треугольника, R – радиус описанной окружности треугольника.

Проверяем себя.

Т1. Какие из данных утверждений верны?

а) Центром     описанной    окружности     треугольника    является                   точка пересечения медиан, проведенных к его сторонам.

б) Вокруг тупоугольного треугольника нельзя описать окружность.

в) Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.

г) Если из точки M проведены две касательные к окружности и А и В — точки касания, то отрезки MA и MB равны.

Ответ: в), г)

Т2.    Какие   три  из   перечисленных   утверждений  верны  для окружности, описанной около треугольника?

а) ее центр лежит в точке пересечения серединных перпендикуляров сторон треугольника;

б) окружность называется описанной около треугольника, если она касается всех его сторон;

в) около любого треугольника можно описать окружность;

г) Ее центр лежит в точке пересечения биссектрис внутренних углов треугольника;

д) Ее радиус вычисляется по формуле      𝑅 = abc

4S

, где a, b, c – стороны

треугольника, S – его площадь;

е) Ее   радиус   вычисляется   по   формуле     𝑅 = 𝑆

𝑃

,   где   S   –   площадь

треугольника, а p – полупериметр.

Ответ: а), в), д)

Т3. Расположите номера заданий по возрастанию полученных в ответах градусных мер углов.

а) Вписанный угол, опирающийся на полуокружность.

б) Центральный угол, который опирается на дугу, равную 1/3 окружности.

в)     Меньший    угол    прямоугольного    равнобедренного            треугольника, вписанного в окружность.

Ответ: в), а), б)

Решаем задачи.

1.     а) Сторона равностороннего треугольника равна 2√3. Найдите радиус окружности, описанной около этого треугольника.

Ответ: 2

б) Сторона равностороннего треугольника равна 4√3. Найдите радиус окружности, описанной около этого треугольника.

Ответ: 4

в) Сторона равностороннего треугольника равна 6 √3 . Найдите радиус окружности, описанной около этого треугольника.

Ответ: 6

2.                       а) Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.

Ответ: 9

б) Радиус окружности, описанной около равностороннего треугольника, равен 10. Найдите высоту этого треугольника.

Ответ: 15

в) Радиус окружности, описанной около равностороннего треугольника, равен 8. Найдите высоту этого треугольника.

Ответ: 12

3.            а) Через концы диаметра окружности проведены две хорды, пересекающиеся на окружности и равные 12 и 16. Найдите расстояния от центра окружности до этих хорд.

Ответ: 8 и 6

б) Через концы диаметра окружности проведены две хорды, пересекающиеся на окружности и равные 26 и 18. Найдите расстояния от центра окружности до этих хорд.

Ответ: 9 и 13

в) Через концы диаметра окружности проведены две хорды, пересекающиеся на окружности и равные 10 и 22. Найдите расстояния от центра окружности до этих хорд.

Ответ: 11 и 5

4.                  а) Радиус окружности, описанной около равностороннего треугольника, равен 2√3 Найдите длину стороны этого треугольника.

Ответ: 6

б) Радиус окружности, описанной около равностороннего треугольника, равен 4√3 Найдите длину стороны этого треугольника.

Ответ: 12

в) Радиус окружности, описанной около равностороннего треугольника, равен 6√3 Найдите длину стороны этого треугольника.

Ответ: 18

5.                   а) Окружность с центром в точке О описана около равнобедренного треугольника АВС, в котором АВ=ВС и ∠АВС = 66 °. Найдите величину угла ВОС. Ответ дайте в градусах.

Ответ: 114

б) Окружность с центром в точке О описана около равнобедренного треугольника АВС, в котором АВ=ВС и ∠АВС = 107 °. Найдите величину угла ВОС. Ответ дайте в градусах.

Ответ: 73

в) Окружность с центром в точке О описана около равнобедренного треугольника АВС, в котором АВ=ВС и ∠АВС = 34°. Найдите величину угла ВОС. Ответ дайте в градусах.

Ответ: 146.

6.             а) Центр окружности, описанной около треугольника

АВС лежит на стороне АВ. Радиус окружности равен

10. Найдите ВС, если АС = 16.

Ответ: 12

б) Центр окружности, описанной около треугольника АВС лежит на стороне АВ. Радиус окружности равен 14,5. Найдите ВС, если АС = 21.

Ответ: 20

в) Центр окружности, описанной около треугольника АВС лежит на стороне АВ. Радиус окружности равен 6,5. Найдите ВС, если АС = 12.

Ответ: 5

7.            а) Сторона АС треугольника АВС проходит через центр описанной около него окружности. Найдите

∠С, если ∠А = 44°. Ответ дайте в градусах.

Ответ: 46

б) Сторона АС треугольника АВС проходит через центр описанной около него окружности. Найдите

∠С, если ∠А = 58^О. Ответ дайте в градусах.

Ответ: 32

в) Сторона АС треугольника АВС проходит через центр описанной около него окружности. Найдите ∠С, если ∠А = 83^О. Ответ дайте в градусах.

Ответ: 7.

Задачи с развернутым ответом.

a.     

Ответ: 2√10.

b.     Точка Н является основанием высоты ВН, проведенной из вершины прямого угла В прямоугольного треугольника АВС. Окружность с диаметром ВН пересекает стороны АВ и СВ в точках Р и К соответственно. Найдите ВН, если РК = 13.

Ответ: 13.

c.      Радиус окружности, вписанной в прямоугольный треугольник, равен 2 см, а радиус окружности, проходящей через все вершины треугольника, равен 5 см. Найдите больший катет треугольника.

Ответ: 8 см.