Поделиться
3.31 Площади многоугольников, изображенных на клетчатой бумаге.docx
Площади многоугольников, изображенных на клетчатой бумаге.
Повторяем теорию.
Чтобы найти площадь фигуры на клеточной бумаге площадь можно оценить квадратами со стороной в 1единичный отрезок, а также можно применить правила и формулы геометрии для нахождения площади фигуры, можно использовать метод вырезания или формулу Пика.
Оценка площади
квадратами со стороной в 1 единичный отрезок.
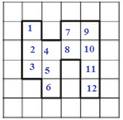
Площадь оценивают квадратами со стороной в 1 единичный отрезок, подсчитывая сетку из таких квадратов в фигуре.
Ответ 12.
Применение правила и формул геометрии для нахождения площади фигуры
Рассмотрим применение правила и формул геометрии на примерах задач:
Пример 1. На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
|
|
Площадь треугольника равна половине произведения его основания на высоту Основание а = 8 клеток, высота h = 3 клетки S= 1 а ∙ha = 1 ∙ 8 ∙ 3= 12 2 2 Ответ 12 |
Пример 2. На клетчатой бумаге с размером клетки
1×1 изображён треугольник. Найдите его площадь.
|
|
Этот треугольник – прямоугольный. Площадь прямоугольного треугольника равна половине произведения его катетов Основание а = 7 клеток, высота b = 9 клеток S= 1 а ∙ b = 1 ∙ 7 ∙ 9 = 31,5 2 2 Ответ 31,5. |
Пример 3. На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите площадь этого параллелограмма.
|
|
Площадь параллелограмма равна произведению его стороны и высоты, проведенной к этой стороне. Сторона а = 5 , высота h = 5 S = a ∙ha = 5∙5 =25 Ответ 25. |
Пример 4. На клетчатой бумаге с размером клетки 1×1 изображён ромб.
Найдите площадь этого ромба.
|
|
Площадь ромба равна половине произведения его диагоналей. Диоганали равны: d1 = 2 клетки, d2 = 10 клеток. S= 1 d1∙d2 = 1 ∙ 2∙ 10 =10 2 2 Ответ 10. |
Пример 5. На клетчатой бумаге с размером клетки
1×1 изображена трапеция. Найдите её площадь.
|
|
Площадь трапеции равна произведению полусуммы её оснований на высоту Основание а = 2 клетки, второе основание b = 6 клеток, высота h = 3 клетки. S= 1 (а + b)∙h = 1 ∙( 2 + 6) ∙ 3= 12 2 2 Ответ 12 |
Метод вырезания.
Площадь
одной клетки равна 1. Найдите
площадь фигуры, изображённой на рисунке.
|
|
Дополним фигуру до прямоугольника. Прямоугольник будет состоять из нашей фигуры- 1 и двух прямоугольных треугольников - 2 и 3. Площадь прямоугольника: S = a∙ b = 6∙6 =36 Площадь прямоугольного треугольника: S2 = 1 а ∙ b = 5∙ 6 :2 = 15 2 Площадь прямоугольного треугольника: S3 = 1∙1 :2 = 0,5 Из площади полученного прямоугольника вычтем площади прямоугольных треугольников: S1 = 36-15-0,5=20,5. Ответ 20,5. |
Формула Пика.
Формула Пика (или теорема Пика) - классический результат комбинаторной геометрии и геометрии чисел, согласно которому площадь многоугольника с целочисленными вершинами равна:
S = В + Г / 2 − 1,
где В - количество целочисленных точек внутри многоугольника, Г - количество целочисленных точек на границе многоугольника. Теорема(формула) Пика доказана Георгом Пиком в 1899 году.
Рассмотрим пример ее применения:
|
|
В =15, Г = 8 S = В + Г / 2 – 1 = 15 + 8:2 -1 = 18
Проверим методом вырезания: S =36 – 1/2∙5∙6 – 1/2∙1∙6 = 18 Ответ 18. |
Проверяем себя.
Т1. На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба. Выберите верный ответ.
Варианты ответа: 1) 6; 2) 24; 3) 12
Ответ 3.
Т2. На клетчатой
бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Выберите верный ответ.
Варианты ответа: 1) 72; 2) 36; 3) 80.
Ответ 2.
Т3. На клетчатой
бумаге с размером клетки
1×1 изображена трапеция. Найдите её площадь. Выберите верный ответ.
Варианты ответа: 1) 14; 2) 7; 3) 28.
Ответ 3.
Решаем задачи.
1 На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
|
а)
Ответ 24. |
б)
Ответ 16. |
в)
Ответ 36. |
2. На клетчатой бумаге с размером клетки 1×1 изображён треугольник.
Найдите площадь этого треугольника.
|
а) Ответ 25. |
б)
Ответ 36. |
в)
Ответ 35. |
3. На клетчатой бумаге с размером клетки 1×1 изображена трапеция.
Найдите площадь этой трапеции.
|
а)
Ответ 42. |
б)
Ответ 28. |
в)
Ответ 36. |
4. На клетчатой бумаге с размером клетки 1×1 изображён треугольник.
Найдите площадь этого треугольника.
|
а)
Ответ 31,5. |
б)
Ответ 16. |
в)
Ответ 16. |
5. На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите площадь этого параллелограмма.
|
а)
Ответ 42. |
б)
Ответ 35. |
в)
Ответ 21. |
6. На клетчатой бумаге с размером клетки 1×1 изображена фигура.
Найдите её площадь.
|
а)
Ответ 17. |
б)
Ответ 9. |
в)
Ответ 14. |
7. На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
|
а)
Ответ 17. |
б)
Ответ 13. |
в)
Ответ 17. |
Задачи с развернутым ответом.
1. Сумма диагоналей ромба равна 70 см, а его периметр равен 100 см. Найдите площадь этого ромба.
Ответ 600 см2.
2. Найдите площадь ромба, периметр которого равен 60 см, а разность диагоналей равна 6см.
Ответ 21 6см2.
3. Найти площадь треугольника ACD. Ответ: 30.
Пример решения задачи с развернутым ответом
Задача 1.Сумма диагоналей ромба равна 70 см, а
его периметр равен 100 см. Найдите площадь этого ромба.
Решение
|
|
По условию ABCD – ромб, где ВD + АС =70; AB+ ВC+ СD +АD = 100, так как стороны ромба равны, то 4AB = 100, АВ =25, АО + ОВ = 70:2 = 35. Рассмотрим прямоугольный треугольник АОВ (АС⊥ ВD по свойству ромба). По теореме Пифагора : АВ2 = АО2 + ВО2. Где АО = 35 – ОВ. Пусть ВО = х. Тогда составим уравнение: (35- х)2 + х2 = 252. |
352 – 70х +х2 +х2 = 252;
2х2 – 70х + 1225 - 625 = 0;
2х2 – 70х + 600 = 0; х2 – 35х + 300 = 0;
х =20 или х = 15, пусть ВО = 20, тогда АО = 35 – 20 =15. Диагонали ВD = 2∙ 20 =40 и АС = 2∙15 = 30.
Площадь ромба равна половине произведения его диагоналей:
S ABCD = 1 ∙ 40∙
30 = 600.
2
Ответ 600 см2.
Задача 2 решается аналогично задаче 1.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
