3.31 Вписанная в четырехугольник окружность

Вписанная в четырехугольник окружность.

Повторяем теорию.

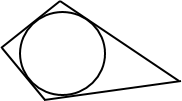Окружность называется вписанной в четырехугольник, если она касается всех его сторон.

В этом случае четырехугольник называют описанным около окружности.

Свойства

1. 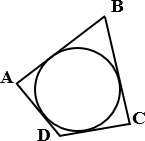    В четырехугольник можно вписать окружность (и притом только одну) в том и только том случае, если суммы длин его противоположных сторон равны.

Окружность вписана в четырехугольник ABCD, следовательно, AD + BC = AB + DC.

2. 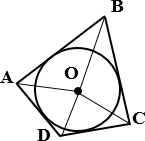    Центром вписанной окружности четырехугольника является точка пересечения его биссектрис.

В четырехугольнике 𝐴𝐵𝐶𝐷, О – центр вписанной окружности, следовательно, ВО, СО, АО, DO – биссектрисы углов,

3.     В параллелограмм можно вписать окружность, только если он является ромбом.

4.     В любой ромб (а значит, и в квадрат) можно вписать окружность; центром этой окружности является точка пересечения диагоналей ромба.

5. 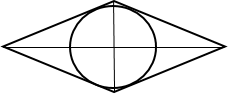    Радиус            окружности, 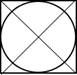вписанной  в  квадрат,

равен половине стороны.

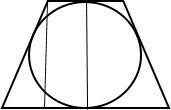
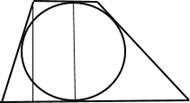
6.     Если в трапецию можно вписать окружность, то диаметр этой окружности равен высоте трапеции.

7.     Площадь S четырехугольника, в который можно вписать окружность (описанного четырехугольника), равна произведению полупериметра p этого четырехугольника на радиус r вписанной окружности этого четырехугольника: S = pr.

Проверяем себя

Т1. Вставьте пропущенные слова:

а) Если четырехугольник описан около окружности, то         . б) В любой                                  можно вписать окружность.

в) Если четырехугольник АВСD вписан в окружность, то          .

Ответ: а) суммы длин его противоположных сторон равны; б) ромб и треугольник; в) АВ + СD = ВС + AD.

Т2. Закончите предложение, выбрав верное равенство.

Окружность вписана в четырехугольник МКОР. Тогда              . а) МК + КО = ОР + РМ;

б)      МК + ОР = КО + РМ; в)  МК + МР = ОК + ОР.

Ответ: б)

Т3. Выберите верные утверждения:

а)        Центр   вписанной   в    четырехугольник   окружности   лежит           на пересечении его серединных перпендикуляров;

б)        Площадь четырехугольника, описанного около окружности – это произведение его полупериметра на радиус вписанной окружности;

в)        В любую трапецию можно вписать окружность;

г)         Центр окружности, вписанной в четырехугольник, является точкой пересечения биссектрис углов четырехугольника;

д)        Высота трапеции, в которую вписана окружность, равна диаметру этой окружности.

Ответ: б), г), д)

Решаем задачи

1.                       а)   Сторона   квадрата   равна   34.   Найдите             радиус окружности, вписанной в этот квадрат.

Ответ: 17

б)    Сторона   квадрата   равна    46.   Найдите       радиус окружности, вписанной в этот квадрат.

Ответ: 23

в) Сторона квадрата равна 48. Найдите радиус окружности, вписанной в этот квадрат.

Ответ: 24

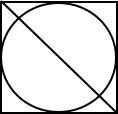
2.       а) Радиус вписанной в квадрат окружности равен 4√2. Найдите диагональ этого квадрата.

Ответ: 16

б) Радиус вписанной в квадрат окружности равен 6√2. Найдите диагональ этого квадрата.

Ответ: 24

в) Радиус вписанной в квадрат окружности равен 8√2. Найдите диагональ этого квадрата.

Ответ: 32

3.              а) Окружность радиуса 9 вписана в квадрат. Найдите площадь квадрата.

Ответ: 324

б) Окружность радиуса 7,5 вписана в квадрат. Найдите площадь квадрата.

Ответ: 225

в) Окружность радиуса 10,5 вписана в квадрат. Найдите площадь квадрата.

Ответ: 441.

4.               а) Радиус окружности, вписанной в трапецию, равен

16. Найдите высоту этой трапеции.

Ответ: 32

б) Радиус окружности, вписанной в прямоугольную трапецию, равен 10. Найдите меньшую боковую сторону этой трапеции.

Ответ: 20

в) Радиус окружности, вписанной в трапецию, равен 23. Найдите высоту этой трапеции.

Ответ: 46

5.       а) Высота трапеции равна 24. Найдите радиус окружности, вписанной в эту трапецию.

Ответ: 12

б) Высота трапеции равна 35. Найдите радиус окружности, вписанной в эту трапецию.

Ответ: 17,5

в) Высота трапеции равна 16. Найдите радиус окружности, вписанной в эту трапецию.

Ответ: 8

6. 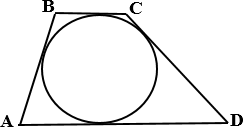             а) Трапеция АВСD с основаниями АD и ВС описана около окружности. АВ = 9, ВС = 7, СD = 11. Найдите АD.

Ответ: 13

б) Трапеция АВСD с основаниями АD и ВС описана около окружности. АВ = 16, ВС = 10, СD = 13. Найдите АD.

Ответ: 19

в) Трапеция АВСD с основаниями АD и ВС описана около окружности. АВ

= 8, ВС = 2, СD = 15. Найдите АD.

Ответ: 21

7. 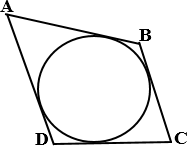             а) В четырехугольник АВСD вписана окружность, АВ = 17, СD = 22. Найдите периметр четырехугольника.

Ответ: 78

б) В четырехугольник АВСD вписана окружность, АВ = 35, СD = 19. Найдите периметр четырехугольника.

Ответ: 108

в) В четырехугольник АВСD вписана окружность, АВ = 24, СD = 99. Найдите периметр четырехугольника.

Ответ: 246

Задачи с развернутым ответом.

a.      Около окружности описана равнобокая трапеция с основаниями 5 и 3. Найдите радиус окружности.

Ответ: 1 √15

2

b.     В равнобедренный треугольник АВС вписана окружность. Параллельно

его основанию АС проведена касательная к окружности, пересекающая боковые стороны в точках D и Е. Найдите радиус окружности, если DЕ = 8, АС = 18.

Ответ: 6.