3.34 Обобщение и систематизация знаний за курс

Занятие по обобщению и систематизации знаний за курс.

Исторические сведения.

«Первые понятия и теоремы»

Возникновение первых геометрических понятий непосредственно связано с повседневной жизнью человека: с измерением полей, строительством жилых зданий и амбаров, с изготовлением и украшением предметов быта.

Уже в далекой древности скребки и ножи изготовлялись в форме ромбов, треугольников, сегментов. Поля обычно имели форму прямоугольника. При строительстве домов и измерений земель выработался ряд правил для обращения с прямыми линиями. Во многих странах людей, которые занимались разделом земли на участке, называли натягивателями веревки. Большинство геометрических терминов произошло от греческих слов, означающих названия конкретных предметов. Так термин «куб» произошел от греческого слова, означающего игральную кость. Термин введен пифагорейцами, затем он встречается у Евклида.

Слово «центр» означало палку с заостренным концом, которой погоняли быков; позднее оно обозначало ножку циркуля, помещенного в центр описываемой окружности.

Термин «ромб» происходит от греческого «бубен», а «трапеция» - от слова «столик».

Термин «точка» происходит от греческого глагола «ткнуть».

В Древнем Египте еще не было терминов «фигура», «сторона фигуры». Использовались слова «поле», «границы поля», «длина» и «ширина» поля. Греческий историк Геродот указывал, что развитие геометрии в Древнем Египте связано с необходимостью после каждого разлива Нила заново распределять поля между их владельцами.

В египетских текстах нет никаких сведений о теореме, которую мы сейчас называем теоремой Пифагора. Однако греческие ученые, побывавшие в Египте, сообщали о том, что там имеется правило для построения прямого угла. Использовалась веревка, разделенная на 12 равных частей. Ее натягивали в виде треугольника со сторонами 3, 4, 5.

Вавилонская геометрия, так же, как и египетская, теснейшим образом связана с практикой. Она использовалась при межевании земель, строительстве домов, плотин, каналов, возведении насыпей. Сохранились планы земельных участков, имеющих форму треугольников, прямоугольников, трапеций.

Итак,   геометрия   древнейших   цивилизаций   была   тесно   связана   с практикой.   Правила   устанавливались интуитивно,      многие   из   них                     были приближенными. Никаких следов рассуждений и доказательств не обнаружено. Совершенно                     иначе выглядела                     геометрия Древней       Греции.                 Она превратилась в науку, основанную на строгих доказательствах. Усвоив все конкретные знания, полученные в Египте и Вавилоне, греки решительным образом порвали с прагматизмом ученых Востока. Они выдвинули на первое

место строгость логического построения, изящество и точность доказательств.

Начало греческой науки положила школа натурфилософии. Ее основатель Фалес доказал, что диаметр делит круг пополам, доказал теорему о равенстве углов при основании равнобедренного треугольника, теорему о равенстве вертикальных углов, а также теорему о равенстве треугольников по стороне и двум прилежащим углам.

«Треугольник»

Первое упоминание о треугольнике и его свойствах мы находим в египетских папирусах, которым более 4000 лет. Через 2000 лет в древней Греции. Древние рисовали треугольники. В древнем искусстве очень широко распространяются изображения равностороннего треугольника и ромба. Первобытные люди штамповали треугольники и ромбы на разных изделиях. Вожди племен североамериканских индейцев носили на груди символ власти: равносторонний треугольник с точкой в центре, в Африке женщины туарегов также украшают себя большими пластинами из равносторонних треугольников. Равносторонние треугольники рисовали - на изображениях священных животных. Также треугольники могут образовать различные символы. Два треугольника, лежащие горизонтально и соприкасающиеся вершинам, - это лунный символ, растущая и убывающая Луна. У алхимиков два треугольника - сущность и субстанция. Треугольники, символизирующие стихии, таковы: огонь (обращенный вершиной вверх), воду (обращенный вершиной вниз), воздух (обращенный усеченной вершиной вверх), землю (обращенный усеченной вершиной вниз). Два смыкающихся треугольника - союз противоположностей, которые становятся «жидким огнем» или «огненной водой».

Крупнейший древнегреческий историк Геродот (V век до нашей эры) оставил описание того, как египтяне после каждого разлива Нила заново размечали плодородные участки его берегов, с которых ушла вода. С этого и началась геометрия – "землемерие" (от греческого "гео" – "земля" и "метрео" "измеряю"). Древние землемеры выполняли геометрические построения, измеряли длины и площади. Астрологи рассчитывали расположение небесных светил – все             это               требовало  весьма        обширных          познаний                  о                свойствах       плоских        и пространственных фигур, и в первую очередь о треугольнике. Изображение треугольников и задачи на треугольники встречаются в египетских папирусах, которым более 4000 лет, в старинных индийских книгах и других древних документах. Уже тогда была известна теорема, получившая впоследствии название теоремы Пифагора, которая применялась для построения прямых углов на местности с помощью веревочного треугольника со сторонами 3, 4, 5

(египетский треугольник).

Известны такие древнегреческие ученые, как Архимед, Пифагор, Фалес. Учение о треугольнике развивалось в ионийской школе, основанной в VII веке до нашей эры Фалесом, затем в школе Пифагора. Древние греки решили упорядочить накопленные сведения о треугольнике и написали много трудов. Наиболее совершенной оказалась работа Евклида "Начала"(365-300 до н.э.).

«Теорема Пифагора»

Пифагор родился в Греции на острове Самос в 576 г.до н.э. Этот остров расположен в Эгейском море. Его учителем был знаменитый ученый того времени - Фалес. Пифагор был очень талантливым учеником, и Фалес понял, что он пойдёт дальше своего учителя. Фалес посоветовал ему отправиться в Египет. Пифагор много времени посвятил путешествию по Восточным странам. В Египте он прожил и набирался мудрости 22 года. Его судьба была не простой. Во время военных походов он был взят в плен и продан в рабство в

Вавилон, где прожил больше 10 лет. Потом Пифагор обосновался в Италии.

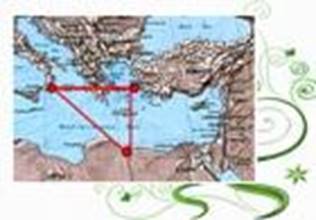
Интересен факт, что если соединить города, где родился (Греция), набирался опыта (Египет) и жил (Италия) Пифагор, отрезками, то на карте получится прямоугольный треугольник.

В те далекие времена зарождались олимпийские игры. Известно, что Пифагор четыре раза был Олимпийским чемпионом. Он был настоящий задира и драчун, и судьи первой в истории олимпиады не хотели допускать его к соревнованиям по кулачному бою. Но он хитростью пробился на состязания и победил всех противников.

Пифагор – это не имя, а прозвище, которое ему дали за то, что он высказывал истину и был великолепным оратором.

Пифагор был из достаточно обеспеченной семьи и на свои деньги организовал собственную школу. Туда брали далеко не всех, а принимали с большими церемониями и после долгих испытаний. Новички могли только из далека слушать голос учителя, видеть же его самого разрешалось только после нескольких лет очищения музыкой и аскетической жизнью. Обучение в школе было двухступенчатое: одних учеников называли «математиками», то есть познавателями, а других - «акусматиками», то есть слушателями. Математики - те, кто изучал суть науки, акусматики - те, кто прослушивал общие сведения из различных наук.

Акусматики обучались на первой ступени в школе Пифагора. Наиболее одаренные и исполнительные из них переводились в математики. Только тогда им разрешалось видеть учителя и вести с ним научные споры и разговоры.

В Пифагорейской школе много внимания уделялось таким наукам, как: музыка, живопись, арифметика, геометрия, астрономия и физическое развитие.

В школе Пифагора была очень строгая дисциплина. Все ученики обязаны были соблюдать целый ряд заповедей. Вот некоторые из них, которые вполне подходят и нам, современным людям:

· Делай то, что впоследствии не огорчит тебя и не принудит раскаиваться

· Не делай никогда того, что не знаешь, но научись всему, что следует знать.

· Не пренебрегай здоровьем своего тела.

Пифагорейцы узнавали друг друга по знаку, который называется пентаграмма (звездчатый пятиугольник. Они верили, что в числовых закономерностях спрятаны великие тайны мира. Пентаграмма считалась в школе Пифагора символом дружбы, была чем-то вроде талисмана, который дарили друзьям; тайным знаком, по которому пифагорейцы узнавали друг друга.

Существует легенда о том, что один из пифагорейцев заболел и больным попал в дом к совсем незнакомым людям. Они старались его вылечить как могли, но болезнь не отступала. Он не мог заплатить им за заботу, и перед смертью попросил их нарисовать на воротах дома пентаграмму, объяснив, что по этому знаку найдутся люди, которые отблагодарят их. И на самом деле, через некоторое время, один из пифагорейцев поинтересовался почему у них этот знак, и услышав рассказ, щедро наградил их.

С Теоремой Пифагора связана известная арифметическая задача: найти натуральные числа, удовлетворяющие уравнению а² + в² = с². Такие числа называются Пифагоровыми тройками.

Применение этой задачи было известно в глубокой древности: в древнем Египте, треугольник со сторонами 3, 4, 5 использовали при разметке прямоугольных земельных участков и при строительстве великий Египетских пирамид.

Сохранилась легенда, согласно которой, доказав свою знаменитую теорему, Пифагор от восторга принёс богам в жертву 100 быков.

Смерть Пифагора тоже окружена красивыми и не однозначными легендами. По одной из них, дом в городе Кротоне, где Пифагор тайно собирался со своими учениками, был специально подожжен недоброжелателями. Преданные друзья бросились в огонь и проложили в нем дорогу учителю, чтобы он мог выйти из огня. Друзья погибли, а сам Пифагор, будучи спасенным такой дорогой ценой, так затосковал, что лишил себя жизни. Умер Пифагор около 500 г. до н. э.

После смерти учителя его школа продолжала существовать и действовать еще в течение нескольких сот лет.

«Равнобедренный треугольник»

Основное свойство равнобедренного треугольника было сформулировано в одной из первых теорем «Начал» Евклида. Кстати, доказательство этой теоремы приписывают Фалесу Милетскому, жившему за 2 века до Евклида. Фалес доказал равенство углов при основании равнобедренного треугольника.

А рассуждал он так: равнобедренный треугольник симметричен относительно биссектрисы угла при вершине, а значит, при перегибании чертежа  по  биссектрисе  углы  при  основании  совпадут. Впоследствии теорема получила название Pons Asinorum, что на латыни означает «мост ослов». Объясняют такое название, с одной стороны, тем, что чертеж, использованный Евклидом для ее доказательства, напоминает мостик, а с другой стороны, – мнением, будто только ослы не могут это мост перейти.

Впрочем, в современно английском языке латинское выражение Pons Asinorum, употребляется в несколько ином смысле – как «Суровое испытание способностей неопытного человека».

«Прямоугольный треугольник»

Прямоугольный треугольник занимает почётное место в вавилонской геометрии, упоминание о нём часто встречается в папирусе Ахмеса. Евклид употребляет выражения: «стороны, заключающие прямой угол», - для катетов;

«сторона, стягивающая прямой угол», - для гипотенузы.

Термин гипотенуза происходит от греческого hypoteinsa, означающего тянущаяся под чем либо, стягивающая. Слово берёт начало от образа древнеегипетских арф, на которых струны натягивались на концы двух взаимно перпендикулярных подставок.

Термин катет происходит от греческого слова «катетос», которое означало отвес, перпендикуляр. В средние века словом «катет» означали высоту прямоугольного треугольника. В XVII веке слово катет начинает применяться в современном смысле и широко распространяется, начиная с XVIII века.

«Параллелограмм»

Термин «параллелограмм» греческого происхождения и, согласно Проклу, был введен Евклидом. Понятие параллелограмма и некоторые его свойства были  известны  еще  пифагорейцам.  В  «Началах»  Евклида  доказывается следующая теорема: в параллелограмме противоположные стороны равны и противоположные углы равны, а диагональ разделяет его пополам. Евклид не упоминает о том, что точка пересечения диагоналей параллелограмма делит их пополам. Полная теория параллелограммов была разработана к концу средних веков и появились в учебниках лишь в XVII веке. Термин «диагональ» происходит от сочетания двух греческих слов «диа» (через) и «гониос» (угол), т.е. прямая, проходящая через вершины углов. Само же понятие параллелограмм от греч. Parallelos – параллельный и gramme – линия. Поэтому слово «параллелограмм» можно перевести как «параллельные линии».

Интересные факты Снимок галактики Centaurus A, сделанный инфракрасным космическим телескопом Spitzer. С его помощью впервые удалось определить структуру пылевого облака в центре галактики. Оказалось, что оно имеет форму параллелограмма.

«Ромб»

Термин    «ромб»    происходит    от др.-греч. ῥόμβος —

«бубен». Если сейчас бубны в основном делают круглой формы, то раньше их делали как раз в форме квадрата или ромба. Поэтому название карточной масти бубны, знаки которой имеют ромбическую форму, происходит ещё с тех времён, когда бубны не были круглыми.

«Квадрат»

Термин «квадрата» происходит от латинского quadratum (quadrare - сделать четырехугольным), перевод с греческого “тетрагонон” - четырехугольник. Квадрат известен во многих древних культурах. Многие исследователи считают, что квадрат – это попытка человека противопоставить организованность и порядок вселенскому хаосу. Как геометрическая фигура, квадрат связан с числом четыре и имеет ряд символических толкований таких, как порядок, мудрость. Он символизировал четыре стороны света, четыре времени года, четыре человеческих возраста. У индийцев квадрат   основной

символ, являющийся стандартом пропорции и идеалом для оценки человека. В греко-римской традиции квадрат являлся символом Афродиты как женской плодородной силы. У пифагорейцев квадрат символизирует душу. У римлян

был специальный термин для гармоничного человека, Homo quadratus человек квадратный, человек гармоничный.

Многие свойства чисел и законов с ними в древности связывали с особыми

фигурами, такими, например, как магический квадрат. Магический, или волшебный квадрат это квадратная таблица, заполненная числами, таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих

диагоналях одинакова. Первые упоминания о магических квадратах были у

древних китайцев. Европейцев с удивительными числовыми квадратами познакомил византийский писатель и языковед Мосхопулос. Его работа была первым специальным сочинением на эту тему и содержала примеры магических квадратов разного порядка, составленных самим автором. В Средневековой Европе, как и на Востоке, магическим квадратам часто приписывали различные магические свойства, поэтому не удивительно, что они пользовались особой популярностью у прорицателей, астрологов и врачевателей. Такие игры как судоку, крестики-нолики, шахматы, шашки, морской бой, пятнашки, кубик Pубик и другие игры основаны на квадратах.

«Трапеция»

«Трапеция» – слово греческого происхождения, означавшее в древности «столик» (по-гречески «трапедзион» означает столик, обеденный стол). «Трапеция» в нашем смысле встречается впервые у древнегреческого математика Посейдона. В средние века трапецией называли, по Евклиду, любой четырёхугольник (не параллелограмм); лишь в XVIII в. это слово приобретает современный смысл.

Созвездие Орион (звезды образуют трапецию).

«Окружность»

В Древней Греции многие свойства фигур, в том числе круга и окружности были сформулированы в виде теорем и доказаны. Наиболее удачно была изложена геометрия, как наука о свойствах геометрических фигур, греческим ученым Евклидом (III в. до н. э.) в своих книгах “Начала”. В Древней Греции круг и окружность считали венцом совершенства. “В каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе”. Это свойство окружности стало толчком к возникновению колеса. Колесо – это чудо! Что же в нём особенного? – подумаете вы. Но это только на первый взгляд. Представьте себе на секунду, что вдруг случилась беда: на Земле исчезли все колёса! Если остановится колесо, то остановится колесо Истории. Остановятся все виды транспорта, остановятся все часы и механизмы, фабрики и заводы. Не произойдет движения вперед.

Самые первые колеса были сделаны в Месопотамии (ныне Ирак) в 3500- 3000 гг. до н. э. и представляли собой гончарный круг и тележное колесо.

Круг и окружность – одни из самых древнейших геометрических фигур, философы древности придавали им большое значение. Круг – воплощение нескончаемого Времени и Пространства, символ всего сущего, Вселенной. “Из всех фигур прекраснейшая – круг”, – считал Пифагор. Круг – “циркулус” – латинское слово, от него же и “циркуль”, без которого бы мы не построили круг. Радиус окружности – это отрезок, соединяющий центр окружности с любой ее точкой (по-латыни – спица колеса). Диаметр окружности – это хорда, проходящая через центр окружности (с греческого – “поперечник”). Хорда окружности – отрезок, соединяющий любые две точки на окружности (с греческого– “струна”).