4. Методические рек к проведению урака. Вариант 1

Методические рекомендации к проведению урока.

Тема урока: Целые числа. Рациональные числа.

Цель обучения:  6.1.1.8 усвоить понятие рационального числа;

6.1.2.9 изображать рациональные числа на координатной прямой;

6.1.2.11 изображать подмножества рациональных чисел с помощью кругов Эйлера-Венна.

Организационный этап, очень кратковременный, определяет весь психологический настрой урока. Психологический настрой проводится для создания благоприятной рабочей обстановки в классе, чтобы дети поняли, что им рады, их ждали. Приветливые, доброжелательные слова учителя, спокойная, уверенная манера являются условием выполнения задач данного этапа.

Приветствие. Попросите учащихся повернуться друг к другу, посмотреть друг-другу в глаза, улыбнуться и пожелать друг-другу хорошего рабочего настроения на уроке. Также учителю рекомендуется пожелать учащимся  работать дружно, открыть что-то новое.

Проверка домашнего задания. Организуйте в виде игры, так как динамичное начало урока служит успешной организации всего урока. Деление учеников по парам: на обрезках бумаги написаны натуральные, целые и рациональные числа. Через сопоставление этих чисел, ученики делятся по парам. Каждая пара делает взаимопроверку тетрадей по готовым ответам, и оценивает комментарием.

Определяется цель урока: Задавая вопросы ученикам, определяю тему урока и цели урока.

8. Как вы думаете какова тема сегоднешнего  урока? Каковы цели?

Тема урока: Целые числа. Рациональные числа.

Цели урока:  усвоить понятие рационального числа;

изображать рациональные числа на координатной прямой; изображать подмножества рациональных чисел с помощью кругов Эйлера-Венна.

Актуализация знаний.

Цель этапа:  включение учащихся в учебную деятельность, создание условий для возникновения внутренней готовности к включению в учебный  процесс. 

Задания для повторения. Действия с рациональными числами.

Да­вай­те про­ве­рим.

·  Сумма двух ра­ци­о­наль­ных чисел все­гда ра­ци­о­наль­ное число: .

·  Раз­ность двух ра­ци­о­наль­ных чисел все­гда ра­ци­о­наль­ное число: .

·  Про­из­ве­де­ние двух ра­ци­о­наль­ных чисел все­гда ра­ци­о­наль­ное число: .

·  Част­ное двух ра­ци­о­наль­ных чисел – ра­ци­о­наль­ное число, за ис­клю­че­ни­ем де­ле­ния на ноль: .

Задания для разминки. Приложение 1.

Раздайте учащимся задания. После организуйте самопроверку по готовым ответам согласно следующим критериям:

Учащийся

- умеет складывать рациональные числа;

- умеет записывать числа в виде обыкновенной дроби;

- знает правила сложения рациональных чисел;

- определяет координату точки М;

- определяет точку по координату;

- знает расположение точек на координатной прямой;

- определяет какая из точек находится дальше от нуля;

- строит координатную прямую;

- отмечает точки на координатной прямой по координатам;

- находит все целые числа;

- определяет количества целых чисел.

Ответы к заданиям для разминки:

Задание 1. Координата точки M (-12).

Задание 2. Точка Р имеет координату 0,5.

Задание 3. Точка   A(−8) находится дальше от нуля.

Задание 4. Учителю рекомендуется нарисовать на доске координатную прямую и вызывать учащихся для изображения заданных точек А(2); В(6,2); С(0); D(-2,2); E; Fна ней.

Задание 5. 9 целых чисел, т.е.: -3; -2; -1; 0; 1; 2; 3; 4; 5.

Изучение новой темы. Рекомендуется освещать новую тему с помощью ярких слайдов для визуализации, приводить примеры из повседневной жизни, чтобы ассоцируя с чем-то легче было запомнить новые понятия, их определения. Также использовать мозговой штурм задавая наводящие вопросы. Например: 

Те­перь мы узна­ли, что такое дроби, на­учи­лись с ними ра­бо­тать. Дробь , на­при­мер, не яв­ля­ет­ся целым чис­лом. Зна­чит, нужно опи­сать новое мно­же­ство чисел, куда будут вхо­дить все дроби, и этому мно­же­ству нужно на­зва­ние, чет­кое опре­де­ле­ние и обо­зна­че­ние.

Нач­нем с на­зва­ния. Ла­тин­ское слово ratio пе­ре­во­дит­ся на рус­ский язык как от­но­ше­ние, дробь. На­зва­ние но­во­го мно­же­ства «ра­ци­о­наль­ные числа» и про­ис­хо­дит от этого слова. То есть «ра­ци­о­наль­ные числа» можно пе­ре­ве­сти как «дроб­ные числа».

Раз­бе­рем­ся, из каких чисел со­сто­ит это мно­же­ство. Можно пред­по­ло­жить, что оно со­сто­ит из всех дро­бей. На­при­мер, таких – . Но такое опре­де­ле­ние было бы не со­всем кор­рект­ным. Дробь – это не само число, а форма за­пи­си числа. В при­ме­ре, пред­став­лен­ном ниже, две раз­ные дроби обо­зна­ча­ют одно и то же число: 

Тогда точ­нее будет ска­зать, что ра­ци­о­наль­ные числа – это те числа, ко­то­рые можно пред­ста­вить в виде дроби. И это в самом деле уже почти то самое опре­де­ле­ние, ко­то­рое и ис­поль­зу­ют в ма­те­ма­ти­ке.

Обо­зна­чи­ли это мно­же­ство бук­вой . А как свя­за­ны мно­же­ства на­ту­раль­ных и целых чисел с новым мно­же­ством ра­ци­о­наль­ных чисел? На­ту­раль­ное число  можно за­пи­сать в виде дроби, при­чем бес­ко­неч­ным чис­лом спо­со­бов . А раз его можно пред­ста­вить в виде дроби, то оно тоже яв­ля­ет­ся ра­ци­о­наль­ным.

С от­ри­ца­тель­ны­ми це­лы­ми чис­ла­ми ана­ло­гич­ная си­ту­а­ция. Любое целое от­ри­ца­тель­ное число можно пред­ста­вить в виде дроби . А можно ли число ноль пред­ста­вить в виде дроби? Ко­неч­но, можно, тоже бес­ко­неч­ным чис­лом спо­со­бов .

Таким об­ра­зом, все на­ту­раль­ные и все целые числа тоже яв­ля­ют­ся ра­ци­о­наль­ны­ми чис­ла­ми. Мно­же­ства на­ту­раль­ных и целых чисел яв­ля­ют­ся под­мно­же­ства­ми мно­же­ства ра­ци­о­наль­ных чисел

().

По­де­лим  на . Среди целых чисел нет та­ко­го, чтобы за­пи­сать ответ: .

Но с по­мо­щью дроб­но­го числа мы почти все­гда можем за­пи­сать ре­зуль­тат де­ле­ния од­но­го це­ло­го числа на дру­гое. По­че­му почти? Вспом­ним, что, по опре­де­ле­нию, де­лить на ноль нель­зя.

Таким об­ра­зом, мно­же­ство ра­ци­о­наль­ных чисел (ко­то­рое воз­ни­ка­ет при вве­де­нии дро­бей) пре­тен­ду­ет на роль мно­же­ства, за­мкну­то­го от­но­си­тель­но всех че­ты­рех ариф­ме­ти­че­ских опе­ра­ций.

 То есть мно­же­ство ра­ци­о­наль­ных чисел за­мкну­то от­но­си­тель­но сло­же­ния, вы­чи­та­ния, умно­же­ния и де­ле­ния, ис­клю­чая де­ле­ние на ноль. В этом смыс­ле можно го­во­рить, что мно­же­ство ра­ци­о­наль­ных чисел устро­е­но «лучше», чем пред­ше­ству­ю­щие мно­же­ства на­ту­раль­ных и целых чисел. Озна­ча­ет ли это, что ра­ци­о­наль­ные числа – по­след­нее чис­ло­вое мно­же­ство, ко­то­рое мы изу­ча­ем? Нет. Впо­след­ствии у нас по­явят­ся дру­гие числа, ко­то­рые нель­зя за­пи­сать в виде дро­бей, на­при­мер ир­ра­ци­о­наль­ных.

·           Координатной прямой называют прямую, на которой заданы положительное направление, начало отсчета (точка О) и единичный отрезок.

·           Каждой точке на координатной прямой соответствует некоторое число, которое называют координатой этой точки. Например, А(5). Читают: точка А с координатой пять.  В(-3). Читают: точка В с координатой минус три.

Демонстрация примеров (слайды 8-9).

Пример 1. Изобразить на координатной прямой точки А(-4,5), В(-2), С(2,5) и D (6).

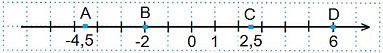
Начертим координатную прямую, за единичный отрезок возьмем 1 клетку. От начала отсчета отложим четыре с половиной клетки влево и поставим точку А. Точка С будет находиться справа от нуля на расстоянии двух с половиной клеток. Точку В отметим на 2 клетки левее точки О, а точку D на 6 клеток правее точки О.

Пример 2. Изобразить на координатной прямой числа: 5; -4; -1; 3; -6; 7. Сравнить с помощью координатной прямой: а) 0 и 5; б) -1 и 7; в) -6 и -4; г) 5 и -6; д) 0 и -6; е) -4 и 3. Сделать выводы.

Выбрав единичный отрезок равным 1 клетке, отметим числа -6, -4 и -1 слева от нуля, а числа 3, 5 и 7 справа от нуля. Меньшее число располагается левее на координатной прямой, а большее — правее.

а) 0<5;      б) -1<7;       в) -6<-4;     г) 5>-6;      д) 0>-6;      е) -4<3.

Нуль больше любого отрицательного числа, но меньше любого положительного числа. Любое отрицательное число меньше любого положительного числа.

На презентации повторить множества натуральных чисел, целых чисел и рациональных чисел.

Если все элементы множества В принадлежат множеству А, то множество В называется подмножеством множества А.

Значит, множества натуральных чисел  является подмножеством множества целых чисел: NZ. Множество целых чисел бесконечно. Множества целых

чисел и положительные и отрицательные дробные числа образуют множество рациональных чисел. Множество рациональных чисел обозначается буквой Q. Термин рационал переводе с латинского "ratio" означает "отношение", "дробь".То что  множество натуральных (N) является подмножеством целых чисел  (Z), а множество целых чисел является подмножеством рациональных чисел (Q) показано кругами Эйлера-Венны, N⊂Z⊂Q.

Леонард Эйлер (1707-1783)-швейцарский математик.

Для проверки знаний провести легкий устный опрос:

№1. Назовите множества:

1) множество чисел, которые используются при счете предмета;

2) множество точек на плоскости равноудаленных от точки О;

3) множества фигур состоящих из двух лучей исходящих из одной точки;

4) множество углов равные 90°.

Задания для закрепления. Рекомендуется для закрепления раздать карточки и провести парную работу. Парная работа дает возможность сэкономить время и обсуждения темы, что способствует более глубокому пониманию новых понятий (Приложение 2). Затем по готовым ответам в слайдах 15-18 провести самооценивание пар по следующим критериям:

Учащийся

- умеет складывать/вычитать/умножать/делить рациональные числа;

- умеет записывать числа в виде обыкновенной дроби;

- знает правила сложения рациональных чисел;

Ответы:

Задание 1.    ; 

Мы выполняли  сложение  рациональных чисел и получили, что сумма  рациональных чисел тоже число   рациональное.

Задание 2.  ; 

Мы выполняли вычитание рациональных чисел и получили, что разность рациональных чисел тоже число рациональное.

Задание 3. ;

Мы выполняли умножение рациональных чисел и получили, что произведение      рациональных чисел тоже число  рациональное.

 Задание 4.  ;  

Мы выполняли деление рациональных чисел и получили, что частное рациональных чисел тоже число рациональное.

После выполнения заданий для закрепления поработать с примером, чтобы научить учащихся переводить периодическую  дробь в обыкновенную.

Пример. Переводите периодическую дробь 0,(4) в обыкновенную.

Решение:  Рас­смот­рим сна­ча­ла дробь, у ко­то­рой пе­ри­од со­сто­ит из одной цифры и нет пред­пе­ри­о­да. Обо­зна­чим это число бук­вой А. Метод за­клю­ча­ет­ся в том, чтобы по­лу­чить еще одно число с таким же пе­ри­о­дом:

Это можно сде­лать, умно­жив ис­ход­ное число на . Итак, число  имеет такой же пе­ри­од. Вы­чтем из  само число :

Для закрепления следует провести самостоятельную работу (Приложение 3).

Учащийся

- умеет записывать числа в виде обыкновенной дроби;

- умеет переводить периодическую дробь в обыновенную;

Ответы:

Задание 1.

Задание 2.

Физкультминутка. Гимнастика для глаз: рисуем «глазами».

Нарисуем два квадрата,

А на них огромный круг,

А потом еще кружочек,

Треугольный колпачок.

Вот и вышел очень, очень

Развеселый чудачок. (Дети рисуют в воздухе «глазами» геометрические фигуры.)

Закрепление. Парная работа (Приложение 4):

Перед выполнением задания, ученики:

а) определяют ход решения задач;

б) совметстно составляют критерий оценивания;

в) пары выходят к доске, решают задачу и объясняют. Остальные учащиеся сравнивают со своими задачами и оценивают по критериям оценивания. (при необходимости, учитель дает обратную связь)

Ответы:

Задание 1. Используя  изображение кругами Эйлера-Венна, покажите что множества натуральных чисел являются подмножеством целых чисел.

Задание 2. Множество членов всех семьи аула- А. Множество детей, которые учатся в школе, всех семьи аула- В. Изобразите множества А и В кругами Эйлера- Венны.

Задание 3. Какие из этих множеств А  В;  С и D является подмножеством множества F?  Изобразите кругами Эйлера-Венны.

Задание 4. Напишите элементы множества D, которое является объединением данных множеств А и В. Изобразите эти множества кругами Эйлера-Венны, соответственно расположите их элементы.

1) А;          В;

D={15, 19. 45, 71, 7, 16, 13}

2) А;                       В

D={a, b, d, 1, 3, 28, 49, 51}

Задание 5.

 Из чисел 6;  -3,5;  8  -9;  -2;  0;  1;  -100;  99 составьте:

1) N-множество натуральных чисел;  {6, 1, 99}

2) Z- множество целых чисел; {6, -9, 0, 1, -100, 99}

3) Q-множество рациональных чисел. {6;  -3,5;  8  -9;  -2;  0;  1;  -100}

Задание 6. (дополнительная задача)

На книжной полке расположены сборник рассказов, сборник песен, сборник сказок и краеведение-всего 26 книг. Сборник рассказов и сборник песен -23 книг. Сборник песен, сборник сказок и краеведение - 17 книг. Сборник рассказов и сборник сказок - 13 книг. Сколько сборников сказок на книжной полке?

Итог урока. Рефлексия.

Учитель повторяет критерий урока:

·         Какая была цель урока?

·         Достиг ли мы этой цели?

Рефлексия.

·                    Что я знал?

·                    Чему научился?

·                    Что было не понятным?

·                    Над чем еще нужно поработать?

Домашнее задание. Приложение 5.

Ссылки:

1.      Алдамуратова Т.А., Байшоланов Т.С., Байшоланов Е.С. Математика.6 класс. В двух частях. Часть1.

2.       https://nsportal.ru/shkola/algebra/library/2013/05/14/ratsionalnye-chislaseriya-urokov

3.      https://www.youtube.com/watch?v=aepErrrSzSY  

4.      https://interneturok.ru/matematika/6-klass/umnozhenie-i-delenie-polozhitelnyh-i-otricatelnyh-chisel/ratsionalnye-chisla

5.      Скачано с www.znanio.ru