4Motion of a charged particle in the magnetic field

Teacher Guides of the Lesson

Theoretical material for the lesson, definitions for concepts 

Figure 1

A bubble chamber image of the tracks of subatomic

particles. The tracks curve because the charged

particles are affected by the presence of a magnetic field.

Moving Moving particles

              The world of atomic physics is populated by a great variety of particles – electrons, protons, neutrons, positrons and many more. Many of these particles are electrically charged, and so their motion is influenced by electric and magnetic fields. Indeed, we use this fact to help us to distinguish one particle from another. Figure shows the tracks of particles in a detector called a bubble chamber. A photon (no track) has entered from the top and collided with a proton; the resulting spray of nine particles shows up as the gently curving tracks moving downwards. The tracks curve because the particles are charged and are moving in a magnetic field. The tightly wound spiral tracks are produced by electrons which, because their mass is small, are more dramatically affected by the field. In this chapter, we will look at how charged particles behave in electric and magnetic fields and how this knowledge can be used to control beams of charged particles. At the end of the chapter, we will look at how this knowledge was used to discover the electron and to measure its charge and mass.

An electron beam tube (Figure 2) can be used to demonstrate the magnetic force on a moving charge. A beam of electrons is produced by an ‘electron gun’, and magnets or electromagnets are used to apply a magnetic field.

You can use such an arrangement to observe the effect of changing the strength and direction of the magnetic field, and the effect of reversing the field. If you are able to observe a beam of electrons like this, you should find that the force on the electrons moving through the magnetic field can be predicted using Fleming’s left-hand rule. In Figure 3, a beam of electrons is moving from right to left, into a region where a magnetic field is directed into the plane of the paper. Since electrons are negatively charged, they represent a conventional current from left to right. Fleming’s left hand rule predicts that, as the electrons enter the field, the force on them will be upwards and so the beam will be deflected up the page. As the direction of the beam changes, so does the direction of the force. The force due to the magnetic field is always at 90° to the velocity of the electrons. It is this force that gives rise to the motor effect. The electrons in a wire experience a force when they flow across a magnetic field, and they transfer the force to the wire itself. In the past, most oscilloscopes, monitors and television sets made use of beams of electrons. The beams were moved about using magnetic and electric fields, and the result was a rapidly changing image on the screen.

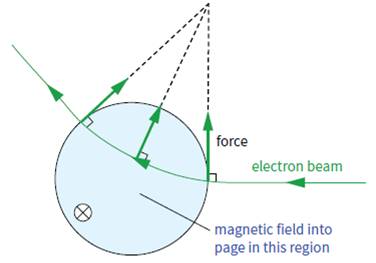
Figure 4

The magnetic force on a moving charge

We can make an intelligent guess about the factors that determine the size of the force on a moving charge in a uniform magnetic field (Figure 4). It will depend on:

■■ the magnetic flux density B (strength of the magnetic field)

■■ the charge Q on the particle

■■ the speed v of the particle.

The magnetic force F on a moving particle at right angles to a magnetic field is given by the equation:

F = BQv

The direction of the force can be determined from Fleming’s left-hand rule. The force F is always at 90° to the velocity of the particle. Consequently, the path described by the particle will be an arc of a circle.

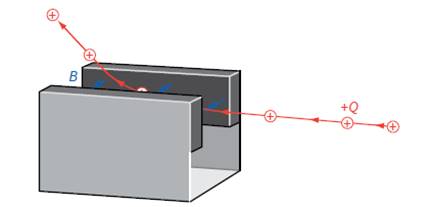
Figure 5

If the charged particle is moving at an angle θ to the magnetic field, the component of its velocity at right angles to B is v sin θ. Hence the equation becomes:

F = BQv sin θ

We can show that the two equations F = BIL and F = BQv are consistent with one another, as follows.

Since current I is the rate of flow of charge, we can write: I = Qt

Substituting in F = BIL gives:                  F = BQL

t

Now, Lt is the speed ν of the moving particle, so we can write:

F = BQv

For an electron, with a charge of −e, the magnitude of the

force on it is:

F = Bev (e = 1.6010⁻¹⁹ C)

The force on a moving charge is sometimes called ‘the Bev force’; it is this force acting on all the electrons in a wire which gives rise to ‘the BIL force’. Here is an important reminder: The force F is always at right angles to the particle’s velocity v, and its direction can be found using the left-hand rule (Figure 5).

Instructions for demonstrations and safety

Warning: experiments with electricity should be performed under the supervision of teachers or adults familiar with electricity safety procedures.

Additional guidelines for organizing a lesson 

1.      Organization moment. Establishing emotional state.  Checking for absent students.

2.      Teacher shows a picture on presentation and asks students: What does “the whole picture” mean? Individual students were called on to respond to questions and share their own opinions/thoughts. Then she explains that the tracks curve because the charged

particles are affected by the presence of a magnetic field.

3.      Teacher introduces the topic and objectives of the lesson, assess criteria.

4.      If a fine beam electron tube is not available,  teacher just uses  a picture of electron beam tube and describes the effects of magnetic fields on moving charges .

5.      Teacher leads learners to derivation of the formula F = BQv sin θ. Use the Fleming’s Left Hand Rule to find the direction of Lorentz force.

6.      Teacher provides students with a mini whiteboard or a A4 paper and markers. As students find the answer for each question, they write and show it to teacher. Teacher check and assess students ability to use Fleming’s left hand rule to determine the velocity of a charge, the direction of the magnetic field, and the direction of the magnetic force on a moving charge.

7.      At the end of the lesson students are encouraged to reflect on what they have learned and

what they need to improve.

Recommendations for formative assessment

Activity1. Students discuss learning objectives and assess criteria.

         Activity2. Individual students were called on to respond to the teacher question related to the

                          picture and share their own opinions/thoughts.

           Activity3. Learners derive the formula by Teacher's Support F = BQv sin θ. Use the Fleming’s 

                           Left Hand  Rule to find the direction of Lorentz force.

         Activity4. Students individually find the answer for each question, they write on the

                          whiteboard/A4 and show it to teacher. They are checked and assessed by a teacher for

                          ability to use Fleming’s left hand rule to determine the velocity of a charge, the

                          direction of the magnetic field, and the direction of the magnetic force on a moving

                          charge.

Activity5. At the end of the lesson students are encouraged to reflect on what they have learned

                and what they need to improve.

Answers, criteria for assignments, additional materials for the lesson

Activity 4.

1. What is the direction of the magnetic force on a positive charge that moves as shown in each of the six cases shown below:

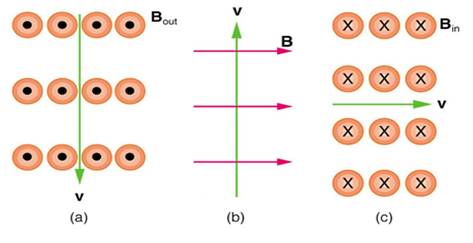
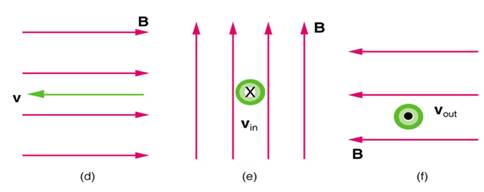
Answers:

 (a) Left (West)

(b) Into the page

(c) Up (North)

(d) No force

(e) Right (East)

(f) Down (South)

2.   What is the maximum force on an aluminum rod with a  charge that you pass between the poles of a 1.50 T permanent magnet at a speed of 5.00 m/s? In what direction is the force?

Answer

F = 7.50∙10^-7 N

Perpendicular to both the magnetic field lines and the velocity

List of useful links and literature 

Douglas C. Giancoli, Physics Principles with Applications, Seventh edition 2014.

David Sang, Graham Jones, Gurinder Chadha and Richard Woodside, Cambridge International    

AS and A Level Physics Course book Second Edition, 2014

https://tap.iop.org/fields/electromagnetism/413/page_46935.html

Скачано с www.znanio.ru