50 Переместительное и Методические рекомендации к уроку. Вариант 2

Методические рекомендации к уроку

Тема урока "Переместительное и сочетательное свойства умножения рациональных чисел"

Цели обучения:

6.1.2.17

применять свойства сложения и умножения рациональных чисел

Критерии оценивания

Учащийся:

знает:

cвойства умножения;

умеет:

использовать переместительное, сочетательное свойства умножения и применяет их при вычислениях.

Теоретический материал:

Если выражение является произведением числа и одной или нескольких букв, то это число называют числовым коэффициентом (или просто коэффициентом).

Например: 5 ∙ а =  5а;  5 — коэффициент.

Коэффициент обычно пишут перед буквенными множителями. Коэффициентом такого выражения, как а или аb, считают1, так как:  а = 1 • а  =  1а;  ab = 1 • ab = 1ab.

При умножении –1 на любое число а получается число –а.

 –1 • a  =  –1a  =  –а.

Поэтому числовым коэффициентом выражения –a считают число –1.

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание:

Решить задания из Приложения 1

1) Сравните:

а) 2³ и 3²; б) (-2)³ и (- 3)²;

в) 1³ и 1²;  г) (-1)³ и (-1)².

Ответ: а) 2³ =8< 3²=9;           б) (-2)³=-8 < (- 3)²=9

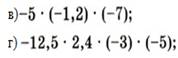
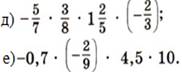
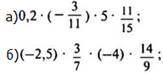2) Найдите значение выражения:

Ответ: а) -0,2; б) ; в) -42; г) -450; д) 0,25; е) 7.

Обсудить решения примеров. Вспомнить какие свойства умножения рациональных чисел использовали при решении.

Совместно с учащимися определить тему и цели урока, зону ближайшего развития.

Работа с классом. Цель: Основываясь на знания законов умножения, ввести понятие числового коэффициента рационального выражения.

На примерах разобрать вопрос.

Пример 1. Упростим выражение 0,3а ∙ (-0,7b).

Р е ш е н и е. Это выражение является произведением четырёх множителей: 0,3∙а∙ (-0,7) ∙ b. Сгруппировав отдельно числовые и отдельно буквенные множители, получим:

0,3а ∙ (-0,7b) = 0,3 ∙ а ∙ (-0,7) ∙ b = (0,3 ∙ (-0,7)) ∙ (а ∙ b) = -0,21 аb.

Число -0,21 называют коэффициентом в полученном выражении.

Если выражение является произведением числа и одной или нескольких букв, то это число называют числовым коэффициентом (или просто коэффициентом).

Коэффициент обычно пишут перед буквенными множителями.

Коэффициентом такого выражения, как а или ab, считают 1, так как a = 1 ∙ а; ab = 1 ∙ ab.

При умножении -1 на любое число а получается число -а: -1 ∙ a = -а.

Поэтому числовым коэффициентом выражения -а считают число -1.

Пример 2. Найдём коэффициент выражения -а ∙ (-b).

Решение. Так как -а∙ (-b) = ab, то, значит, коэффициентом выражения -а∙(-b) является 1.

Пример 3. Найдите коэффициент произведения: 

а) – 6,3 ∙ a ∙ 10 = - 63 а;         коэффициент: -63

б) 3 ∙ (– x) ∙ 27= - 81х;           коэффициент: -81

3x ∙ (–4y) = -12xy;                 коэффициент: -12

2a ∙ (–2b) = -4ab.                    коэффициент: -4.

Пример 4. Упростите выражение и подчеркните его числовой коэффициент:

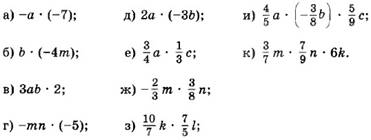
Ответ:  

Для закрепления, при наличии компьютера, просмотреть презентацию для визуального закрепления материала.

Групповая работа.

Объединить учащихся в разноуровневые группы по 4 - 6 учеников. Раздать каждой группе карточки с заданиями.

Приложение 2

1) Упростите выражение:

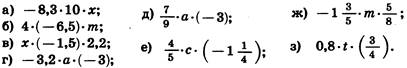
Ответ: .

2) Найдите коэффициент произведения:

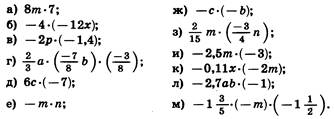
Ответ: ;и)7,5;к)0,22;л)2,7;м)-2,4.

3) Определите знак коэффициента:

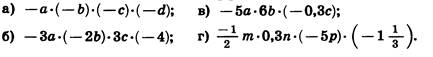
Ответы: а) больше нуля; б) меньше нуля; в) больше нуля; г) меньше нуля

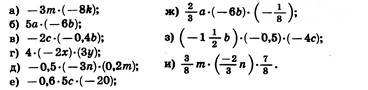
Учитель проходит по рядам, слушает, при необходимости корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям

Каждая группа демонстрирует свой результат выполнения задания..

Старший группы оценивает вклад каждого, выставляя отметку.

Беседа. Рефлексия.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных группах (разного уровня обучаемости). Ученики, распределяя в группе задания, самостоятельно выбирают уровень сложности.

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания на нахождение произведения, коэффициента выражения, используя законы умножения.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

"Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

"Математика 6", Алдамуратова Т.А, Байшоланов Т.С.;

Математика. 6 класс Виленкин Н. Я.;

Самостоятельные и контрольные работы, Ершова А.П., Голобородько В.В. 

Интернет ресурсы:

http://www.yaklass.ru

https://school-assistant.ru