58 Арифметические действия Методическое указание к уроку Вариант 2

Методические рекомендации к уроку

Тема урока "Арифметические действия над рациональными числами"

Цели обучения:

6.1.2.22

находить значения числовых выражений, содержащих рациональные числа.

Критерии оценивания

Учащийся:

знает:

·         правила при действиях с рациональными числами;

·         свойства действий.

умеет:

·         применять правила действий с рациональными числами.

Теоретический материал:

Правила округления десятичной дроби

При округлении дробной части десятичной дроби пользуемся правилами округления.

1.      Подчёркиваем цифру округляемого разряда.

2.      Вертикальной чертой отделяем все цифры, стоящие справа от округляемого разряда.

3.      Если справа от подчёркнутой цифры стоит цифра 0, 1, 2, 3 или 4, то подчёркнутую цифру оставляем без изменений, а все цифры после вертикальной черты отбрасываем.

4.      Если справа от подчёркнутой цифры стоит цифра 5, 6, 7, 8 или 9, то к подчёркнутой цифре добавляем 1, а все цифры после вертикальной черты отбрасываем.

Если при округлении десятичной дроби последняя из оставшихся цифрой в дробной части оказывается 0, то отбрасывать этот ноль нельзя.

Так как в таком случае данный ноль в дробной части показывает, до какого разряда округлено число.

Если десятичную дробь нужно округлить до разряда выше единиц (десятков, сотен и т.д.), то дробная часть отбрасывается, а целая часть округляется по правилам округления натуральных чисел.

Ход урока

На данную тему выделено 4 часа. Можно построить уроки следующим образом:

1 урок: десятичные приближения обыкновенных дробей и действия с ними;

2 урок: улучшить навыки счета и скорость вычисления - решение примеров на все действия;

3 урок: упрощение выражений, решение уравнений;

4 урок: различные задания на рациональность счета и умение применять свойства арифметических действий над рациональными числами.

На каждом уроке желательно используя игровые приемы проверять скорость вычисления.

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание.

Предлагается в игровой форме команде или группе учащихся выполнить ряд однотипных заданий на скорость и правильность вычисления.

Выполнить устно упражнения из Приложения 1.

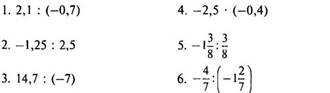
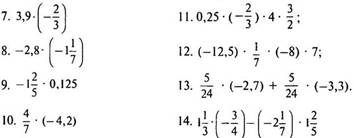
Можно в зависимости от обучаемости класса дать 6 заданий. Если вычислительные навыки хорошие и скорость выполнения высокая, то - все задания.

Совместно с учащимися определить тему и цели урока, «зону ближайшего» развития.

Работа с классом. 1) Вспомнить свойства действий над рациональными числами.

Провести игру «Кто быстрее». Можно сделать в виде рулетки, в случае ошибки, ученик должен озвучить правило, которое необходимо для данного действия, или попросить помощь друга. Приложение 2

Вычислите.

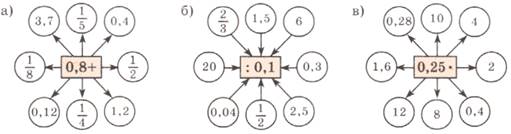
2)  В интерактивном режиме (метод "Активный класс") ввести понятия приближение по недостатку и приближение по избытку. В практике чаще вместо обыкновенных дробей удобнее использовать десятичные дроби. Рассмотрим, как округлить десятичную дробь.

Десятичную дробь можно округлить как до целых, так и до разрядов дробной части: десятых, сотых, тысячных и т.д.

Важно помнить и не путать названия разрядов до и после запятой в десятичной дроби.

Рассмотрим, как округлить десятичную дробь. Десятичную дробь можно округлить как до целых, так и до разрядов дробной части: десятых, сотых, тысячных и т.д.

Важно помнить и не путать названия разрядов до и после запятой в десятичной дроби. В числе 7396,1248 определим названия разрядов.

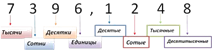
Правила округления десятичной дроби

При округлении дробной части десятичной дроби пользуемся правилами округления.

1. Подчёркиваем цифру округляемого разряда.
2. Вертикальной чертой отделяем все цифры, стоящие справа от округляемого разряда.
3. Если справа от подчёркнутой цифры стоит цифра 0, 1, 2, 3 или 4, то подчёркнутую цифру оставляем без изменений, а все цифры после вертикальной черты отбрасываем.
4. Если справа от подчёркнутой цифры стоит цифра 5, 6, 7, 8 или 9, то к подчёркнутой цифре добавляем 1, а все цифры после вертикальной черты отбрасываем.

Округлим 41,958до сотых.

Округлим 0,748до десятых.
0,7|48 ≈ 0,7
Округлим десятичную дробь 14,89 до разряда единиц в целой части.

Если при округлении десятичной дроби последняя из оставшихся цифрой в дробной части оказывается 0, то отбрасывать этот ноль нельзя.

Так как в таком случае данный ноль в дробной части показывает, до какого разряда округлено число.

Пример. Округление 5,038 до десятых.

5,0|38 ≈ 5,0

Еще один пример:

Обратите внимание, что в примере, в разряде сотых стоит цифра 9, которая при добавлении 1, превращается в 10. Поэтому вместо 9 записываем ноль, а к разряду десятых (у нас это 8) прибавляем 1.

Если десятичную дробь нужно округлить до разряда выше единиц (десятков, сотен и т.д.), то дробная часть отбрасывается, а целая часть округляется по правилам округления натуральных чисел.

Пример. Округлим 837,89 до десятков.

83|7,89 ≈ 840

Правило: Если первая отбрасываемая цифра меньше пяти, то нужно брать приближение по недостатку; а если первая отбрасываемая цифра больше или равна пяти, то нужно брать приближение по избытку.

Результаты округления числа

826,4739:

до тысячных – 826,474;

до сотых – 826,47;

до десятых – 826,5;

до единиц (до целых) – 826;

до десятков – 830;

до сотен – 800;

до тысяч – 1000.

Открыть учебное пособие "Математика 6", прочитать теорию к теме, сравнить свои составленные определения с текстом, оценить правильность рассуждений, при необходимости откорректироать информацию.

Групповая работа. Объединить учащихся в разноуровневые малые группы. Раздать каждой группе карточки с заданиями. Решая задания, учащиеся закрепляют десятичные приближения обыкновенных дробей и действия с ними. 

После выполнения заданий, учащиеся проводят взаимопроверку правильности выполнения заданий по образцу, выданному учителем. Если в классе несколько одинаковых групп по уровням усвоения, то можно провести взаимопроверку групп.

Учащиеся в группе делят между собой задания, после выполнения осуществляют взаимопроверку перед тем как отчитаться о выполнении.

Приложение 3

1.      Указать приближение десятичной дроби 35,472 с недостатком с точностью:

а) до одной единицы; б) до одной десятой; в) до одной сотой.

Решение. а) 35,472 ≈ 35; б) 35,472 ≈ 35,4; в) 35,472 ≈ 35,47.

2.      Указать приближение десятичной дроби 82,608 с избытком с точностью:

а) до одной единицы; б) до одной десятой; в) до одной сотой.

Решение. а) 82,608 ≈ 83; б) 82,608 ≈ 82,7; в) 82,608 ≈ 82,61.

3.      Округлить десятичную дробь 27,417:

а) до единиц; б) до десятых; в) до сотых.

а) 27,417 ≈ 27; б) 27,417 ≈ 27,4; в) 27,417 ≈ 27,42.

4.      Округлить десятичную дробь:

а) 437,15 до единиц; б) 11,985 до десятых; в) 21,288 до сотых.

Решение. а) 437,15 ≈ 437; б) 11,985 ≈ 12,0; в) 21,288 ≈ 21,29.

5.      Округлить десятичную дробь а = 1928,3745:

а) до единиц;       б) до десятых;           в) до сотых;   г) до тысячных;

д) до десятков;    е) до сотен;                ж) до тысяч.  

Решение.

а) а ≈ 1928;           б) а ≈ 1928,4;            в) а ≈ 1928,37;           г) а ≈ 1928,375;

д) а ≈ 1930;          е) а ≈ 1900;                ж) а ≈ 2000.

Приближённые вычисления

6.      Округлить числа а и b с точностью до 0,01, вычислить приближённо сумму а + b и разность а - b:

а) а = 5,437; b = 2,294; б) а = 39,249; b = 1,739.

7.      Округлить числа а и b с точностью до трёх значащих цифр, вычислить приближённо произведение а ∙ b и частное а : b. Результат округлим с точностью до трёх значащих цифр:

а) а = 36,28; b = 5,184; б) а = 71,25; b = 5,612.

Решение.

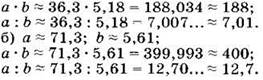
8.      Стороны прямоугольника измерили приближённо: а ≈ 11,9 м, b ≈ 5,29 м. Вычислить приближённо:

а) периметр прямоугольника с точностью до десятых долей метра;

б) площадь прямоугольника с точностью до трёх значащих цифр.

Решение.

а) Периметр прямоугольника со сторонами а и b равен Р = 2(а + b). Округлить длину b до десятых: b ≈ 5,3 м — и вычислить приближённо периметр: Р ≈ 2(11,9 + 5,3) = 34,4 (м).

б) Площадь прямоугольника со сторонами а и b равна S = аb. Вычислить приближённо площадь: S ≈ 11,9 ∙ 5,29 = 62,951 ≈ 63,0 (м²).

Ответ. а) Р ≈ 34,4 м; б) S ≈ 63,0 м².

9.      Найти значение выражения

Решение. Так как то

10.  Заполнить таблицу:

Учитель проходит по рядам, слушает, при необходимости задает дополнительные вопросы, корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям. Каждая группа демонстрирует свой результат выполнения заданий.

Старший группы оценивает вклад каждого, выставляя отметку.

Беседа.

Вопрос 1.Что является десятичным приближением обыкновенной дроби?

(правило повторяют про себя, затем рассказывают в парах, потом всему классу)

1.Десятичная дробь, полученная округлением значения бесконечной дроби

Вопрос 2.Сколько способов десятичного приближения обыкновенной дроби узнали? Какие?

Три способа:

1.Округление с учетом первой отбрасываемой цифры,

2. Округление без учета первой отбрасываемой цифры с сохранением округляемого разряда.

3. Округление без учета первой отбрасываемой цифры с увеличением округляемого разряда на 1.

Вопрос 3. Что такое приближение с недостатком? С избытком? Каковы свойства этих приближений? Как иначе называются эти приближения?

Вопрос 4. Какая цифра называется первой значащей? Второй? Третьей? Как найти значащие цифры числа? Как произвести округление числа до данной значащей цифры?

Рефлексия. Вписать свое мнение об уроке и теме занятия.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости). Ученики, распределяя в паре задания, самостоятельно выбирают уровень сложности.

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить значение приближений десятичных дробей, умеет производить арифметические действия.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

"Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

"Математика 6", Алдамуратова Т.А, Байшоланов Т.С.;

Самостоятельные и контрольные работы, Ершова А.П., Голобородько В.В.