5Нелинейные уравнения с двумя переменными_КСП

Урок №1

Раздел долгосрочного плана: Уравнения, неравенства с двумя переменными и их системы

Школа:

Дата:

ФИО учителя:

Класс 9

Количество присутствующих:

отсутствующих:

Тема урока

Нелинейные уравнения с двумя переменными

Цели обучения, которые достигаются на данном  уроке (ссылка на учебную программу)

 9.2.2.1 различать линейные и нелинейные уравнения с двумя переменными;

Цели урока

Дать понятие геометрического смысла уравнения с двумя переменными. Сформировать понятие о том, что множество решений уравнения с двумя переменными является бесконечное множество точек, находящихся на графике уравнения. Научиться определять по заданному уравнению, какая фигура является его графиком;  «читать» графики и выполнять построение графиков по заданному уравнению с двумя переменными

Критерии оценивания

Учащийся достиг цели обучения, если

ü  Определяет нелинейные уравнения с двумя переменными;

ü  Различает линейные и нелинейные уравнения с двумя переменными;

ü  Использует геометрический смысл уравнения с двумя переменными

Языковые цели

Учащиеся  будут:

обосновывать  выбор  метода и комментировать  процесс  решения  системы  уравнений.

Лексика и терминология, специфичная для предмета:

уравнение  второй степени - second degree equation;

нелинейное уравнение - nonlinear equation;

система уравнений - system of equations;

решить уравнений – to solve of equations;

график уравнения -  equation graph.

Полезные выражения для диалогов и письма:

Решим систему уравнений способом…; выразим одну переменную через другую…; подставим полученное  выражение…; умножим обе части уравнения…; сложим почленно…; найдем соответствующее значение второй переменной….

Привитие ценностей

Уважение, толерантность, сотрудничество, взаимоуважение, патриотизм, честность.

Ученики должны будут участвовать в диалоге, особенно с коллегами в парной работе и участвовать в обсуждении класса, развивая коммуникативные навыки.

Межпредметные связи

 -

Навыки использования ИКТ

Навыки использования интернет-ресурсов, интерактивной  доски

Предварительные знания

Знание  методов решения уравнения,  систем уравнений и неравенств; владение навыками построения графиков.

Ход урока

Запланированные этапы урока

Запланированная деятельность на уроке

Ресурсы

Урок 1

Начало урока

0-2 мин

1.Орг.момент.

2. Тема и цели урока, критерии оценивания.

Слайд №2 -3

Середина урока

2-4 мин

4-7 мин

7-9 мин

9-11 мин

11-21 мин

21-27 мин

25- 34мин

34-36

К Актуализация  знаний

Вопросы на повторение:

1)      Как записывается линейное уравнение с двумя переменными в общем виде?

(ax+by+c=0)

2)      Какая линия описывается  уравнением

 ?

(окружность радиуса  с центром )

 (Графический метод, метод сложения, метод подстановки)

3)      Ответьте ДА или НЕТ. Является ли уравнение линейным?:

Дескриптор: различает линейные и нелинейные уравнения с двумя переменными

Различие между линейными и нелинейными уравнениями с двумя переменными

Уравнение с двумя переменными, в котором хотя бы одно слагаемое содержит переменную в степени отличной от единицы или состоит из произведения переменных, называется нелинейным уравнением.

Например, уравнение 2x + 3y = 5 – линейное, а уравнения 2x² + 3y = 5 и 2x + 3y² = 5 – нелинейные.

Степень уравнения.

Степенью уравнения с двумя переменными называется наибольшая сумма показателей степеней одного одночлена среди всех слагаемых многочлена.

Например, уравнение x(x + y²) = x + 1 есть уравнение третьей степени, так как его можно преобразовать в уравнение xy² + x² – x – 1 = 0, правая часть которого является многочленом третьей степени стандартного вида.

Решение нелинейных уравнений с двумя переменными

Уравнение с двумя переменными, в котором хотя бы одно слагаемое содержит переменную в степени отличной от единицы или состоит из произведения переменных, называется нелинейным уравнением.

Нелинейное уравнение с двумя переменными может иметь одно, несколько или бесконечно много решений, или не иметь решений вовсе.

Графиком нелинейного уравнения с двумя переменными называется множество точек, координаты которых служат решениями этого уравнения. Графиком нелинейного уравнения с двумя переменными является кривая.

Например, графиком уравнения y = ax² + bx + c (a ≠ 0) является парабола, y = x³ – кубическая парабола, xy = k (k ≠ 0) – гипербола, x² + y² = R² – окружность.

То есть решением уравнения с двумя переменными называют множество упорядоченных пар значений переменных, образующих это уравнение в верное равенство.

Уравнения с двумя переменными имеет, как правило, бесконечно много решений. Исключения составляют, например, такие уравнения, как х²+( у²- 4 )²= 0 или

2х²+ у²= 0.

Первое из них имеет два решения (0; -2) и (0; 2), второе – одно решение (0;0).

Уравнение х⁴+ у⁴+3 = 0 вообще не имеет решений. 

Два уравнения, имеющие одно и тоже множество решений, называют равносильными уравнениями. Например, уравнение х(х + у²) = х + 1 есть уравнение третьей степени, так как его можно преобразовать в уравнение ху² + х²- х-1 = 0, правая часть которого – многочлен стандартного вида третьей степени.

Графиком уравнения с двумя переменными называется множество точек, координаты которых служат решениями этого уравнения.

Например, графиком уравнения 2у - х² = -2

является парабола:

И

Учащиеся выполняют задания индивидуально.

Упражнение 1

Является ли пара чисел (-2;3) решением уравнения:

a)  

b)

c)

d) ?

Дескрипторы:

- понимает, что множество упорядоченных пар значений переменных, образующих это уравнение в верное равенство.

Упражнение 2

Сколько решений имеют данные уравнения?

a)  

b)

c)

d)

c)

e)

Дескрипторы:

- Понимает, что нелинейное уравнение с двумя переменными может иметь одно, несколько или бесконечно много решений, или не иметь решений вовсе.

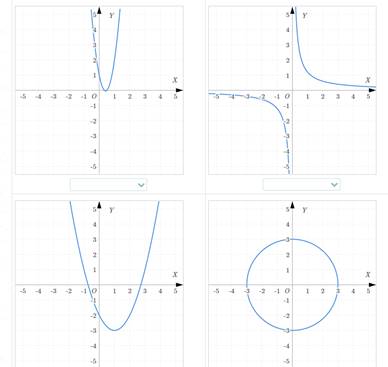
Упражнение 3

Приложение 1

Упражнение 4

Какой кривой (гиперболой, окружностью, параболой) является множество точек, если уравнение этой кривой имеет вид

a)

b)

c)

Дескрипторы:

- Определяет гиперболу

- Определяет окружность

- Определяет параболу

П

Исследовательская  работа

Покажите, что графиком уравнения

 х² + у² + 2х – 8у + 8 = 0 

является окружность  и постройте ее

Инструкция:

1) сгруппируйте слагаемые, содержащие переменную х и содержащие переменную у, и представим каждую группу слагаемых в виде полного квадрата трехчлена

2) запишите в виде квадрата суммы (разности) двух выражений полученные трехчлены;

3) проанализируйте, согласно правилам преобразования графиков уравнений с двумя переменными;

4) постройте график согласно правилам преобразования

Дескрипторы:

1) группирует слагаемые, выделяя полные квадраты;

2) находит центр и радиус окружности;

3) строит окружность.

Ответ:  (х² + 2х + 1) + (у²-2·4·у + 16) + 8 – 1 – 16 = 0;

(х + 1)² + (у – 4)² = 3²; графиком данного уравнения является окружность с центром в точке (-1; 4) и радиусом 3 единицы.

И

Каждый учащийся выполняет задания из рабочего листа

Учащиеся обмениваются рабочими листами и выполняют проверку.

Слайд №4

Слайд №5-8

Bilimland.kz

Слайд №10

Bilimland.kz

Слайд №11

Конец урока

36-40  мин

 Задание на дом: Шыныбеков А.Н. 9 класс Алгебра, п.1

Рефлексия

На лучах у солнца с правой стороны напишите, что у вас сегодня на уроке получилось хорошо, а с левой, что вы бы хотели развить.

Подведите итоги  по целям обучения и критериям оценивания

Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?

Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?

Здоровье и соблюдение техники безопасности

Дифференциация обучения происходит при выполнении индивидуальных заданий

ФО проводится через наблюдение за работой групп, а также через письменные работы учащихся

Здоровьесберегающие технологии.

Используемые физминутки и активные виды деятельности.

Пункты, применяемые из Правил техники безопасности на данном уроке.

Рефлексия по уроку

Были ли цели урока/цели обучения реалистичными?

Все ли учащиеся достигли ЦО?

Если нет, то почему?

Правильно ли проведена дифференциация на уроке?

Выдержаны ли были временные этапы урока?

Какие отступления были от плана урока и почему?

Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки. 

Общая оценка

Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)?

1:

2:

Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)?

1:

2:

Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?