Методические рекомендации к уроку

Тема урока "Статистические данные и их характеристики: среднее арифметическое, мода, медиана, размах."

Цели обучения:

6.4.3.1

знать определения среднего арифметического нескольких чисел, размаха, медианы и моды ряда числовых данных;

6.4.3.2

вычислять статистические числовые характеристики;

Критерии оценивания

Учащиеся

 знают:

□     как находить основные статистические характеристики: среднее арифметическое чисел, размах ряда данных, моду и медиану данных.

умеют

□     находить основные статистические характеристики: среднее арифметическое чисел, размах ряда данных, моду и медиану данных.

Теоретический материал

Статистика - это наука, занимающаяся сбором, обработкой, анализом количественных данных о разнообразных массовых явлениях, происходящих в природе и обществе.

Слово статистика переводится с латинского языка status- состояние, положение вещей.

Статистические характеристики: среднее арифметическое, размах, мода, медиана.

Среднее арифметическое - это сумма всех чисел разделенная на их количество. (Среднее арифметическое называют средним значением числового ряда.)

Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел.

Мода ряда чисел – это число, которое встречается в данном ряду чаще других.

Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание.

Задача. 12 шестиклассников попросили отметить время (в минутах) затраченное на выполнение домашнего задания по математике. Получили следующие данные: 23,18,25,20,25,25,32,37,34,26,34,25.

Сколько минут в среднем учащиеся потратили на выполнение домашнего задания? Как определить среднее время?

Когда нужно и где нужно определить среднее данное?

Часто определяют средние затраты в семье на продукты, среднюю урожайность картофеля на огороде, средние расходы на продукты, чтобы понять, как поступать в следующий раз, чтобы не было большого перерасхода,  среднюю оценку за четверть – по  ней поставят оценку за четверть.

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Работа с классом. Ввод в тему урока.

Определение. Статистика - это наука, занимающаяся сбором, обработкой, анализом количественных данных о разнообразных массовых явлениях, происходящих в природе и обществе.

Статистика изучает численность отдельных групп населения страны и её регионов, производство и потребление разнообразных видов продукции, перевозку грузов и пассажиров различными видами транспорта, природные ресурсы и т. п.

Изучим основные понятия статистики: среднее арифметическое, размах ряда чисел, мода ряда чисел, медиану.

Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.

Пример: Найдем среднее арифметическое для чисел 5,24, 6,97, 8,56, 7,32 и 6,23.

(5,24+6,97+8,56+7,32+6,23):5=6.864.

Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.

Размах ряда 5,24, 6,97, 8,56, 7,32, 6,23 равен 8,56-5,24=3.32

Модой ряда чисел называется число, которое встречается в данном ряду чаще других.

Модой ряда 32, 26, 18, 26, 15, 21, 26 является число 26, встречается 3 раза.

Медианой упорядоченного ряда чисел

а) с нечетным числом членов называется число, записанное посередине;

б)а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.

Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.

Первичное закрепление: Дан ряд натуральных чисел: 2, 3, 3, 4, 1, 1, 2, 5, 1.

Найти статистические характеристики ряда.

Среднее арифметическое ряда (сумма всех чисел ряда поделить на количество): 11.

Размах ряда данных (разность между наибольшим и наименьшим значениями ряда): 4.

Мода (значение, встречающееся наибольшее количество раз): 1.

Медиана: 1) расположить данные в порядке возрастания или убывания, 2) если количество чисел четное, то выбрать величину расположенную в середину ряда, если количество чисел нечетное, то найти среднее арифметическое двух чисел, расположенных в середине ряда) 1,1,1,2,2,3,3,4,5. Количество чисел нечетно, в середине ряда стоит число - 2. Медиана равна 2.

Индивидуальная работа. Для закрепления и оценки усвоения пройденного материала предложить учащимся задания подобные заданиям Приложения 1. Каждый выполняет самостоятельно.

Приложение 1

Найти статистические характеристики ряда чисел.

1) Дан ряд: 30, 5, 23, 5, 28, 30

Среднее арифметическое чисел: (30+5+23+5+28+30):6=20

Размах ряда: 30-5=25

Моды ряда: 5 и 30

Медиана ряда: 25.5

2) Дан ряд: 40, 35, 30, 25, 30, 35

Среднее арифметическое чисел: (40+35+30+25+30+35):6=32,5

Размах ряда: 40-25=15

Моды ряда: 30, 35

Медиана ряда: 32.5

3) Дан ряд: 1, 7, 3, 8, 7, 12, 22, 7, 11,22,8.

Среднее арифметическое чисел:

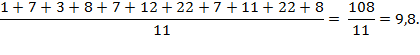
Размах ряда: 22-1=21.

Мода ряда: Чаще всего в этом ряде чисел встречается число 7 (3 раза). Оно и является модой данного ряда чисел.

Медиана ряда: расположить данные в порядке возрастания: 1, 3, 7, 7, 7, 8, 8, 11, 12, 22, 22.

Количество чисел 11 - нечетно, в середине ряда стоит число - 8. Медиана равна 8.

После окончания выполнения, попросить обменяться тетрадями с соседом. Взаимопроверка по ключу. Собрать информацию о выполнении. Разобрать задания, которые были сделаны с ошибками.

Дальнейшее закрепление провести в группах.

Групповая работа. Объединить учащихся в разноуровневые малые группы. Раздать каждой группе карточки с заданиями.

Приложение 2

I) Найти статистические характеристики данного ряда отрицательных и вещественных чисел.

1) Дан ряд: 67,1, 68,2, 67,1, 70,4, 68,2.

Среднее арифметическое чисел: (67,1+68,2+67,1+70,4+68,2):5=68,2.

Размах ряда: 70,4-67,1=3,3.

Моды ряда: 67.1, 68.2.

Медиана ряда: 68.2.

2) Дан ряд: 0,6, 0,8, 0,5, 0,9, 1,1.

Среднее арифметическое чисел:  (0,6+0,8+0,5+0,9+1,1):5=0.78.

Размах ряда: 1,1-0,5=0.6.

Ряд не имеет моды.

Медиана ряда: 0.8.

3) Дан ряд: -21, -33, -35, -19, -20, -22.

Среднее арифметическое чисел:  ((−21)+(−33)+(−35)+(−19)+(−20)+(−22)):6=−25.

Размах ряда: (-19)-(-35)=16.

Ряд не имеет моды.

Медиана ряда: -21,5.

4) Дан ряд: -4, -6, 0, -4, 0, 6, 8, -12.

Среднее арифметическое чисел: ((−4)+(−6)+0+(−4)+0+6+8+(−12)):8=−1,5.

Размах ряда: 8-(-12)=20.

Моды ряда: -4, 0.

Медиана ряда: -2.

5) Дан ряд: 275, 286, 250, 290, 296, 315, 325.

Среднее арифметическое чисел: (275+286+250+290+296+315+325):7=291.

Размах ряда: 325-250=75.

Ряд не имеет моды.

Медиана ряда: 290.

II) Ответьте на вопросы и сделайте выводы.

1) Всегда ли можно найти среднее арифметическое?

- Можно найти для любого конечного ряда чисел найти среднее арифметическое из любого множества чисел.

2) Может ли среднее арифметическое ряда чисел не совпадать ни с одним из этих чисел? 

- Среднее арифметическое может не совпадать ни с одним из этих чисел.

3) Любой ли ряд чисел имеет моду? 

- Ряд чисел может не иметь моды.

4) Может ли ряд чисел иметь более одной моды? Приведите примеры.

- Числовой ряд может иметь более одной моды.

Ряд чисел может иметь более одной моды, а может не иметь моды совсем.

В ряду чисел 5,24, 6,97, 8,56, 7,32 и 6,23 моды нет.

Ряд 1, 1, 2, 2, 3 содержит 2 моды: 1 и 2.

5) Может ли мода ряда чисел не совпадать ни с одним из этих чисел?

-Мода, если она существует, обязательно совпадает с двумя или более числами ряда.

6) Может ли медиана числового ряда не совпадать ни с одним из этих чисел?

Медиана ряда чисел может не совпадать ни с одним из этих чисел.

            Учитель проходит по рядам, слушает, при необходимости задает дополнительные вопросы, корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям. Каждая группа демонстрирует свой результат выполнения заданий.

Старший группы оценивает вклад каждого, выставляя отметку.

Беседа. Рефлексия.

Вопросы   учащимся:

– Когда и где нужны статистические характеристики?

В конце урока учащиеся проводят рефлексию, прикрепляя стикер со своим именем на слайде и или на бумаге, прикрепленной к доске.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

1.      "Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

2.      "Математика 6", Алдамуратова Т.А, Байшоланов Т.С.; Алматы. «Атамура». 2011 год.

3.      Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192

4.      Г.В.Дорофеев, Л.Г. Петерсон. Математика. 6 класс. Часть 3. Москва. Ювента. 2011 год.

5.      "Математика 6" Н.Я.Виленкин, Жохов В.И, Чесноков А.С. и др., Москва «Мнемозина», 2010г.

Интернет ресурсы:

1.      http://www.yaklass.ru

2.      https://school-assistant.ru