6.4А-5. Решение комбинаторных задач Методические рекомендации к уроку

Методические рекомендации к уроку

Тема урока "Решение комбинаторных задач методом перебора."

Цели обучения:

6.4.2.1

решать комбинаторные задачи методом перебора.

Критерии оценивания

Учащиеся

 знают:

как решать комбинаторные задачи методом перебора.

умеют

решать комбинаторные задачи методом перебора;

Теоретический материал

Комбинаторика – раздел математики, в котором изучается, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Решить комбинаторную задачу – это значит выписать все возможные комбинации, составленные из чисел, слов, предметов и др., отвечающих условию задачи.

Задачей комбинаторики считают  задачу размещения объектов по специальным правилам и нахождение числа способов таких размещений.

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание.

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Работа с классом. Ввод в тему урока.

Комбинаторика – раздел математики, в котором изучается, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов. Начальнику цеха надо распределить несколько видов работ между  имеющимися станками, агроному – разместить посевы сельскохозяйственных культур  на нескольких полях, заместителю директора школы – составить расписание уроков, ученому- химику – рассмотреть возможные связи между атомами и молекулами, лингвисту - учесть различные варианты значений букв незнакомого языка и т.д.

Очень часто и нам в жизни приходится делать выбор, принимать решение. Это сделать очень трудно, потому что   приходится выбирать из множества возможных вариантов,  различных способов, комбинаций. И нам всегда хочется, чтобы этот выбор был правильным.  В этом нам помогают комбинаторные задачи, решая которые  мы учимся думать необычно, оригинально, смело.

Задачей комбинаторики считают  задачу размещения объектов по специальным правилам и нахождение числа способов таких размещений.

Сегодня рассмотрим с вами некоторые задачи комбинаторики. Мы научимся определять ход их решения, а также познакомимся и научимся на практике несколько методов решения комбинаторных задач.

Познакомимся с методом перебора, деревом возможных вариантов для решения комбинаторной задачи. Решить комбинаторную задачу – это значит выписать все возможные комбинации, составленные из чисел, слов, предметов и др., отвечающих условию задачи.

Простые задачи решают обыкновенным полным перебором  возможных вариантов без составления различных таблиц и схем. Решение задачи методом полного перебора всех возможных вариантов.

Приложение 1

1) Сколько двузначных чисел можно составить, используя цифры  1; 4; 7?

Решение: Для того, чтобы не пропустить и не повторить ни одного из чисел, будем выписывать их в порядке возрастания:
11; 14; 17; (начали с 1)
41; 44; 47; (начали с 4)
71; 74; 77; (начали с 7)

Таким образом, из трёх данных цифр  можно составить всего 9 различных двузначных чисел.

Ответ: 9 чисел.

2) Сколько трёхзначных чисел можно составить, используя цифры 3 и 5?

3) В школе проводятся соревнования по хоккею. В качестве призов решили использовать мячи, ракетки, клюшки и шайбы. Сколько различных призов можно составить из этих предметов, если каждому победителю решено давать по 2 разных предмета?

4) В четверг  в первом классе должно быть 3 урока: русский язык, математика и физкультура. Сколько различных вариантов расписания можно составить на этот день?

Групповая работа. Объединить учащихся в разноуровневые малые группы. Раздать каждой группе карточки с заданиями.

Приложение 2

Задача 1. Из дома Буратино в театр ведут три дороги, и из театра в школу ведут еще три дороги. Сколькими способами может Буратино пройти в школу, посетив театр?

Решение. Покажем на рисунке схематически.

Метод перебора: Д1Т1; Д1Т2; Д1Т3; Д2Т1; Д2Т3; Д2Т2; Д3Т1; Д3Т2;Д3Т3.

3 ∙ 3 = 9

Ответ: 9.

Задача 2. Буратино пришел в школу и встретил своих друзей Арлекин, Пьеро, Мальвину. Они все обменялись рукопожатиями. Сколько всего рукопожатий было?

Решение.

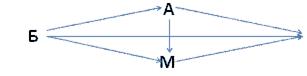
Метод перебора.

БА; БП; БМ; АП; АМ; ПМ.

Если Буратино пожал руки троим друзья, то Арлекин и Буратино обменялись рукопожатиями, значит, Арлекин еще пожмет руки Пьеро и Мальвине, а Мальвина еще пожмет Пьеро руку.

3 + 2 + 1 = 6

Ответ: 6

Если бы у Буратино была не только Азбука, но и еще 4 учебника, то как бы он решил следующую задачу.

Мальвина любит своим друзьям задавать сложные вопросы. У нее было с собой четыре яблока. Она решила угостить своих друзей. Но прежде чем это сделать задала им задачу. Давайте поможем героям сказки решить ее.

Задача 3. Сколькими способами Мальвина может раздать яблоки своим друзьям, если она может все отдать одному или распределить их по своему желанию?

Решение.

Методом перебора.

Чтобы легче было перебрать все варианты  составим таблицу.

Ответ: 15.

Задача 4. В финальном забеге на 100 м участвуют Буратино, Арлекин и Пьеро. Назовите возможные варианты распределения призовых мест.

Ответ:
Вариант 1: 1) Буратино, 2) Арлекин, 3) Пьеро.
Вариант 2: 1) Буратино, 2) Пьеро, 3) Арлекин.
Вариант 3: 1) Пьеро, 2) Буратино, 3) Арлекин.
Вариант 4: 1) Пьеро, 2) Арлекин, 3) Буратино.
Вариант 5: 1) Арлекин, 2) Пьеро, 3) Буратино.
Вариант 6: 1) Арлекин, 2) Буратино, 3) Пьеро.

Учитель проходит по рядам, слушает, при необходимости задает дополнительные вопросы, корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям. Каждая группа демонстрирует свой результат выполнения заданий.

Старший группы оценивает вклад каждого, выставляя отметку.

Беседа. Рефлексия.

Вопросы   учащимся:

– Что значит «решить комбинаторную задачу»?

В конце урока учащиеся проводят рефлексию, прикрепляя стикер со своим именем на слайде и или на бумаге, прикрепленной к доске.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

1.      "Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

2.      "Математика 6", Алдамуратова Т.А, Байшоланов Т.С.; Алматы. «Атамура». 2011 год.

3.      Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192

4.      Г.В.Дорофеев, Л.Г. Петерсон. Математика. 6 класс. Часть 3. Москва. Ювента. 2011 год.

5.      Математика - 6» автор Н.Я.Виленкин, Жохов В.И, Чесноков А.С. и др., Москва «Мнемозина», 2010г.

Интернет ресурсы:

1.      http://www.yaklass.ru

2.      https://school-assistant.ru