6.4D-2. Фигуры в пространстве. Методические рекомендации к уроку

Методические рекомендации к уроку

Тема урока " Расположение фигур в пространстве. Изображение пространственных фигур, «невидимые» линии. Понятие вектора "

Цели обучения:

6.3.2.4

распознавать фигуру по её изображению и изображать плоские и пространственные фигуры;

Критерии оценивания

Учащиеся:

- комментируют  построение развёрток;

- описывают выбор изображения фигуры при повороте;

- обосновывают построение видов сверху, спереди, слева.

Теоретический материал:

Определение.

Ход урока

Организационный момент.

Проверить домашнее задание. При необходимости разобрать примеры, вызвавшие затруднения.

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Актуализация опорных знаний.

Какие стереометрические фигуры вам известны?

• куб
• цилиндр
• шар
• конус
• пирамида
• параллелепипед

Работа с классом. Организовать учащихся по оформлению чертежей по построению развёрток, описанию изображения фигуры, обоснованию построения видов сверху, спереди, слева. Они знакомятся правилами изображения фигур в пространстве в ходе выполнения следующих заданий.

Стереометрия - раздел геометрии, изучающий положение, форму, размеры и свойства пространственных фигур.

Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять. Простейшие фигуры в пространстве: точка, прямая, плоскость.

Плоскость. Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны. На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области. Известно, что через три точки, не лежащие на одной прямой, можно провести одну плоскость.

Учащийся изображает скрытые линии фигур пунктиром; на чертеже сохраняет параллельность прямых и соотношение параллельных отрезков.

Приложение 1.

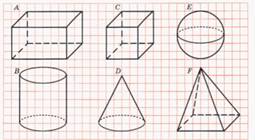
Задание 1. Какие геометрические фигуры изображены на рисунке? Перерисуй их по клеточкам в тетрадь.

Расскажите о правилах изображения фигур в пространстве?

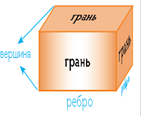
Задание 2. Рассмотрите рисунок и дайте определения элементов фигур.

Элементы прямоугольного параллелепипеда:

-       - Всего 6 граней: 2 основания, 4 боковые грани.

-       - Всего 12 ребер: 8 ребер основания, 4 боковых ребра.

- Вершин - 8.

Длины трех ребер, пересекающихся в одной вершине прямоугольного параллелепипеда,  называются его измерениями. Это: длина, ширина и высота.

Примерные вопросы для обсуждения:

- сколько граней (плоских сторон) у куба? сколько углов? сколько рёбер? Какой формы эти грани?

- сколько граней/углов/ребер у призмы? цилиндра? конуса? Какой формы эти грани?

- у какой трёхмерной фигуры нет ни одного угла? Спросите у учащихся - что они заметили, рассматривая предметы со всех сторон. Учащиеся должны заметить, что все грани являются прямоугольниками и что противоположные грани равны между собой. Чтобы уметь различать прямоугольный параллелепипед от куба приготовьте две его модели: с прямоугольным основанием и с квадратным основанием.

Прямоугольный параллелепипед и куб еще называют и призмой. Про это ты побольше узнаешь в старших классах. Некоторые учащиеся могут путать прямоугольный параллелепипед с квадратным основанием и куб. С помощью макетов ознакомьте с элементами параллелепипеда (куба) и их названиями (грани: основания и боковые грани; ребра: ребро основания и ребро боковой грани; вершины), предложите учащимся с помощью фломастера или маркера покрасить эти элементы на макете. Например, вершины красным цветом, ребра синим цветом, а грани желтым цветом. Затем, используя цвета, пусть подсчитают количество каждого элемента. Чтобы не запутаться, посчитав одну и ту же вершину или ребро два раза, можно предложить класть пальцы по одному на вершины. А при подсчете ребер предложите сначала посчитать количество ребер верхнего основания, умножить его на два и затем прибавить число боковых граней. Такой навык в будущем пригодится при определении количества ребер у призмы.

После ознакомления с элементами прямоугольного параллелепипеда перейдите к вопросу о том, как можно начертить параллелепипед.

Приложение 2.

Практическая работа.

Для этого предлагается проведение следующей практической работы:

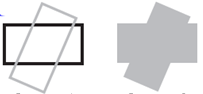
Наложите друг на друга две проволочные модели прямоугольника как на 1, и спросите: «все ли стороны обеих прямоугольников видны?».

Начертите рисунок на доске.

Теперь точно также наложите друг на друга два одинаковых прямоугольника из бумаги (размеры такие же, как у проволочных моделей), и повторите вопрос (рисунок 2). На доске нарисуйте рисунок 2, спросите – чего не хватает, т.е. объясните, что если на рисунок посмотрит другой человек, то он может не понять, что это два наложенных друг на друга прямоугольника. Дайте задание, чтобы каждый ученик на белом листе бумаги показал свой вариант дополнения рисунка. Выбрав среди ответов наиболее удачно нарисованный рисунок, обратите внимание учащихся на то, что принято видимые ребра чертятся сплошной линией, а невидимые – пунктирной.

Теперь обратите внимание учащихся на две модели прямоугольного параллелепипеда: сделанная из проволоки и сделанная из бумаги. Затем показав на доске рисунок 3, спросите: какой модели соответствует каждый из рисунков.

Рисунок 3

Обратите внимание учащихся на основания, а также на правую и левую грани параллелограмма, 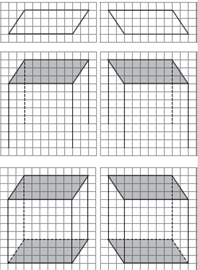изображенного на первом рисунке.

Задайте вопрос: «На модели это прямоугольники, а на рисунке почему наклонно (учащиеся еще не знают параллелограмм) нарисованы?». Учащиеся должны понять, что изображение на плоскости пространственных фигур зависит от ракурса, с которого смотрят на фигуру. Следующее ваше действие направьте на пополнение рисунка второй модели. Учащиеся должны заметить, что на рисунке не хватает пунктирных линий. Если они этого не заметят, задавайте наводящие вопросы. После этого попросите их на обратной стороне листа, на котором они рисовали предыдущий рисунок, нарисовать второй рисунок, дополнив его необходимыми линиями. Учащихся, которые правильно сделали рисунок, объедините в группы с теми учениками, которые допустили ошибки, и организуйте взаимное обсуждение.

Перейдите к рисованию прямоугольного параллелепипеда и куба, используя клетки тетради. Рисование лучше начать с изображения основания. Для этого используйте рисунки из учебника. Обсудите какой рисунок может служить изображением основания прямоугольного параллелепипеда.

Теперь к одному из выбранных рисунков (2,3,4) проведите боковые ребра, обсудите – сколько боковых ребер будет начерчено сплошной линией, а сколько – пунктирной, и спросите – какие боковые ребра обязательно будут изображены сплошной линией. Также обратите внимание на длины боковых ребер: какими могут быть их длины, могут ли они быть разными?

Дополнение остальных рисунков дайте на индивидуальное выполнение. Если ученик сначала рисует внешний каркас, а потом только проводит пунктирные линии, то это показывает, что он не может правильно представить себе пространство. Поэтому, дайте такому ученику следующее руководство:

Руководство

1) рисуется основание прямоугольного параллелепипеда

2) с каждой вершины нарисованного основания проводятся боковые ребра одинаковой длины: три ребра сплошной линией, одно - пунктирной

3) последовательно соединяя вторые концы боковых ребер, получаем другое основание параллелепипеда: две стороны основания – сплошные линии, две – пунктирные

Задание. Дорисуй рисунки в тетради так, чтобы получился прямоугольный параллелепипед:

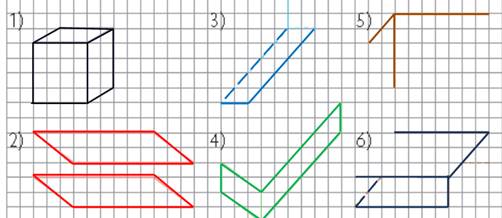
При дополнении рисунков используются линии клетчатой тетради. Самое главное, не надо забывать, что на рисунке пунктирными линиями даны невидимые линии. Рисунок 4 возможно вызовет трудности у учащихся. Поэтому, предложите этот пункт выполнить на доске такому ученику, который хорошо освоил тему. А остальные рисунки предлагается дать на самостоятельное выполнение в тетрадях.

Групповая работа. Для выполнения следующих упражнений разделите учащихся на малые группы, для того чтобы они обсудили задание и выполнили его совместно. При выполнении задания учащиеся анализируют условие, в ходе обсуждения развивают математическую речь, самостоятельно принимают решение, развивают навыки работы в команде.

Первые пять пунктов этого задания дайте для устного выполнения. А последний пункт предлагается решать у доски, так как в процессе выполнения этого задания учащиеся знакомятся с терминами боковая поверхность, полная поверхность. Если с помощью ИКТ будете показывать искомые площади на параллелепипеде, то это будет способствовать лучшему запоминанию учащимися.

Приложение 3

1) Какими фигурами являются грани прямоугольного параллелепипеда? (прямоугольники)

2) Основание прямоугольного параллелепипеда может быть квадратом. (показать макет) Боковая грань может ли быть квадратом? (После ответа учащихся расположите макет горизонтально.) А две его боковые грани, имеющие общее ребро? (в это случае прямоугольный параллелепипед будет кубом)

3) Сколько ребер, сколько граней и сколько вершин имеет куб? (12 ребер, 6 граней, 8 вершин)

4) Какое предложение верно?:

А. Все кубы являются прямоугольным параллелепипедом.

В. Все прямоугольные параллелепипеды являются кубом.

5) Какие элементы куба являются равными между собой? А у прямоугольного параллелепипеда? (У куба все грани равны между собой и все ребра равны между собой. А у прямоугольного параллелепипеда только противоположные грани равны. Боковые ребра равны между собой.)

6) У прямоугольного параллелепипеда с измерениями 7 см × 4 см × 10 см:

– чему равна площадь одного основания? (при выполнении этого задания учащиеся должны учитывать - какая грань параллелепипеда является его основанием. Поэтому есть три возможных ответа: 28 см², 40 см², 70 см²)

– чему равна площадь каждой боковой грани? (смотрите указание в ответе предыдущей задачи: 28 см² и 40 см² или 70 см² и 40 см² или 28 см² и 70 см²)

– вычисли сумму площадей всех боковых граней.

Это называют боковой поверхностью прямоугольного параллелепипеда. (136 см² или 220 см² или 196 см²).

– вычисли сумму площадей всех граней. Это называют полной поверхностью прямоугольного параллелепипеда. (276 см²)

– чему равен объем? (280 см³).

Ввод нового термина: Плоская фигура, состоящая из шести равных квадратов, соединенных сторонами, называется гексамино.

Существует 35 различных форм гексамино, но только 11 из них являются развертками куба.

 Если есть возможность, покажите на экране фигуры гексамино в увеличенном виде. Затем предложите попробовать с помощью пространственного воображения определить среди 35 фигур 11 разверток куба.

По ссылкам:  https://youtu.be/dKis0mNrAaY или

http://www.etudes.ru/ru/ etudes/cubisme/ покажите видео и при этом учащиеся будут проверять свои ответы. Если есть ошибки, то рекомендуется выяснить их причины и сделать исправления.

В диалоге сделать следующий вывод с учащимися: Площадь развертки будет площадью полной поверхности параллелепипеда

Приложение 4.

Задание 1. Мысленно сверните из фигур гексамино куб и определите, какая грань является верхней, если нижняя грань закрашена?

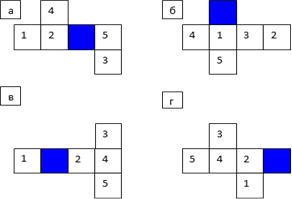  Ответ: а) 1; б) 5; в) 4; г) 4

Задание 2. Какие из фигур не могут быть развертками куба?

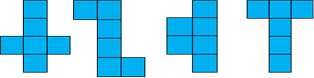
     a                   b                     c                     d

 Ответ: фигура c

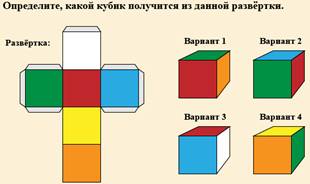
Задание 3. Разверткой какого куба является данная развертка?

Задание 4.

Вывод определений и названия элементов фигур.

ПРИЗМА (греческое prisma — отпиленное  бревно) - многогранник, две грани которого (основания) — равные многоугольники, расположенные в параллельных плоскостях, а другие грани (боковые) — параллелограммы.

Ребра, не лежащие в основаниях призмы, называются боковыми ребрами. Призма, боковыми гранями которой являются прямоугольники, называется прямой. В противном случае призма называется наклонной.

Прямая призма, основаниями которой являются правильные многоугольники, называется правильной. Призмы бывают треугольные, четырехугольные, пятиугольные и т. д. в зависимости от того, какие многоугольники лежат в их основаниях — соответственно треугольники, четырехугольники, пятиугольники и т. д. Дайте учащимся задание: найти определения фигур, с рисунками в Интернете. Подготовить сообщение о следующих фигурах.

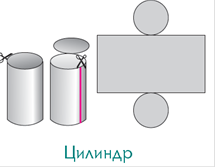
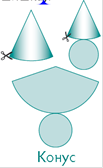
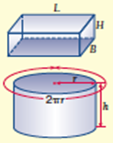
Наблюдайте за работой учащихся, если необходимо корректируйте их деятельность. По окончании времени каждая группа представляет свою работу классу.

Работа в парах. Учебное пособие «Математика 6». Решить задачи по учебнику на изучаемую тему: "Расположение фигур в пространстве. Изображение пространственных фигур, «невидимые» линии. Задания по цели обучения на повторение основных знаний, полученных по теме, оформляя их в соответствии с требованиями. Взаимооценивание: ученики оценивают доступность объяснения при взаимообучении. Взаимопроверка по ответам.

Рефлексия. Рефлексия.

По итогам полученных ответов примите решение о повторном изучении, закреплении темы или продолжении изучения материала по программе.

Домашнее задание.  Обязательное домашнее задание по целям обучения 6.3.2.4

 «Фигуры в пространстве» предполагает количество заданий, на выполнение которых учащиеся должны затрачивать не более 15-20 минут. Задания для выполнения дома рекомендуем дифференцировать по уровню сложности, включая задания на анализ, синтез и оценку. При этом, желательно, давать учащимся задачи практического содержания: решить из уровня В учебного пособия «Математика 6» №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Скачано с www.znanio.ru