6.4В-14.Прямая пропорциональностьк. Методические рекомендации к уроку

Методические рекомендации к уроку

Тема урока "Прямая пропорциональность и её график"

Цели обучения:

6.1.2.23

распознавать прямо пропорциональные зависимости и приводить примеры;

6.2.1.12

знать формулу и строить график прямой пропорциональности;

6.5.2.11

интерпретировать графики реальных зависимостей между прямо пропорциональными величинами;

6.5.2.12

записывать формулу прямой пропорциональности по описанию;

6.5.2.13

строить график прямой пропорциональности;

Критерии оценивания

Учащиеся:

знают

·         как распознать прямо пропорциональные зависимости и привести примеры;

·         как по формуле строить график прямой пропорциональности;

умеют

·         интерпретировать графики реальных зависимостей между прямо пропорциональными величинами;

·         записывать формулу прямой пропорциональности по описанию;

·         строить график прямой пропорциональности;

Теоретический материал:

Определение. Две величины называются прямо пропорциональными, если их отношение равно конкретному, отличному от нуля числу, то есть: , тогда .

Определение. Зависимость вида y=kx называется прямой пропорциональностью.

Число k называется коэффициентом пропорциональности.

Ход урока

Организационный момент.

Проверить домашнее задание. При необходимости разобрать примеры, вызвавшие затруднения.

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Актуализация опорных знаний. Фронтальный опрос. Следить за активностью класса.

Приложение 1.

Задание 1. Пусть известно, что турист двигается со скоростью 2 км/ч от некоторого пункта А к другому пункту В. Определить пройденный им путь каждый час и какова будет формула зависимости:  (1)

Задание 2. Если известно, что пассажир едет на поезде от некоторого пункта А к другому пункту В, а поезд движется со скоростью 60 км/ч, то в каждый час определить удаление пассажира от начального пункта и определить формулу зависимости:   (2)

Работа с классом. Вспомнить определения прямой и обратной пропорциональности:

Определение 1. Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.

Определение 2. Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.

Основываясь на опыт, приобретенный на предыдущих уроках, ввести формулы прямой пропорциональности. В общем виде формулы в предыдущих заданиях можно представить как  y=kx. Не важно, что подразумевают под собой переменные х и у, важно только, что одна из них независимая, например время, а вторая зависимая, например расстояние.

Определение. Две величины называются прямо пропорциональными, если их отношение равно конкретному, отличному от нуля числу, то есть: , тогда .

Определение: Зависимость вида  называется прямой пропорциональностью.

Число  называется коэффициентом пропорциональности.

В общем виде формулы 1 и 2 можно представить как .

Отсюда  – это одна из физических интерпретаций углового коэффициента.

Если перейти к формуле прямой пропорциональности, то

Построим графики   и– обе функции это прямая пропорциональность. Графиком является прямая. Для построения прямой (графика) достаточно двух точек. (Почему?)  Построим графики этих функций, для этого составим таблицы.

Таблица для функции :

Таблица для функции :

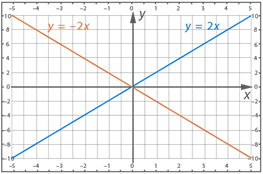
Вывод: Графиком линейной функции y=kx является прямая, проходящая через начало координат.

Из формулы y=kx получим, что .

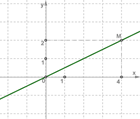
Поэтому для определения коэффициента k достаточно взять любую точку на прямой и найти отношение ординаты этой точки к её абсциссе.

Прямая проходит через точку M(4;2), а для этой точки имеем  Значит, k=0,5, и данная прямая является графиком линейной функции y=0,5x.

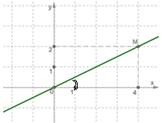График линейной функции y=kx обычно строят так: берут точку (1;k) (если x=1, то из равенства y=kx выводим, что y=k) и проводят прямую через эту точку и начало координат.

Иногда вместо точки (1;k) можно взять другую точку, более удобную.

От коэффициента k зависит угол, который построенная прямая образует с положительным направлением оси x.

Если k>0, то этот угол острый (как на первом рисунке),

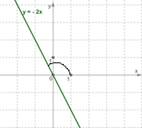а если k<0, то этот угол тупой (как на втором рисунке).

Поэтому коэффициент k в записи y=kx называют  угловым коэффициентом.

Угловой коэффициент является аналогом скорости в формуле движения.

Одна из основных задач – это уметь находить угловой коэффициент в различных выражениях.

Найти угловой коэффициент:

 , значит, что .

 ;      , тогда   .

А также, что если , то угол между графиком функции и положительным направлением оси х тупой и функция убывает, а если k>0 – угол острый и функция возрастает, это видно из графиков. Физический аналог этому такой: если турист ушел из дома и его скорость равна 2 км/ч, то в каждый момент времени расстояние от него до дома увеличивается, а если сказать, что расстояние выражается как , это значит, что он возвращается домой и расстояние сокращается.

Закрепление провести в группах.

Групповая работа. Для выполнения следующих упражнений разделите учащихся на малые группы, для того чтобы они обсудили задание и выполнили его совместно. При выполнении задания учащиеся анализируют условие, в ходе обсуждения развивают математическую речь, самостоятельно принимают решение, развивают навыки работы в команде.

Приложение 2

Задание 1.

а) Постройте графики прямой пропорциональности по данным значениям в таблице правильно выбрав оси координат.

б)  Выберите формулу, которая соответствует каждой задаче в предыдущем задании:

v = ;    t = ;    s = 3t;    P = 3a;    a = ;    S = 3a;    b = .

Ответ: S = 3t                                                          P = 3a                                                S = 3a

Задание 2.

а) Пешеход, двигаясь с постоянной скоростью 3 км/ч, прошёл 9 км. Какое расстояние пройдёт пешеход, если его время движения увеличить в 2 раза? уменьшить в 1,5 раза?

б) Ширина прямоугольника равна 3 см, площадь 15 см². Как изменится площадь прямоугольника, если длину увеличить в 2 раза? уменьшить в 2,5 раза?

в) Сторона равностороннего треугольника равна 3 см. Как изменится его периметр, если сторону увеличить в 2 раза? уменьшить в 1,5 раза?

Задание 3. Ответив на вопросы, сделать вывод.

Что общего во всех формулах?

S = 3t;   P = 3a;   S = 3a.

- Что вы использовали при выполнении задания?

– Что интересного вы заметили в построении графиков? (Все графики одинаковые отрезки.)

- Что общее в формулах? (Они задают прямую пропорциональную зависимость.)

- Запишите общую формулу прямой пропорциональности.

- Что является графиком прямой пропорциональности?

В данных заданиях график прямой пропорциональной зависимости:

y = kx график — луч с началом в точке (0; 0)

Наблюдайте за работой учащихся, если необходимо корректируйте их деятельность. По окончании времени каждая группа представляет свою работу классу.

Работа в парах.  Учебное пособие «Математика 6». Решить задачи по учебнику на изучаемую тему: задания по цели обучения 6.1.2.23, 6.2.1.12, 6.5.2.11, 6.5.2.12, 6.5.2.13

«Прямая пропорциональность и её график», на повторение основных знаний, полученных по теме, оформляя их в соответствии с требованиями. Взаимооценивание: ученики оценивают доступность объяснения при взаимообучении. Взаимопроверка по ответам.

Рефлексия. Для формативного оценивания примените технику «Светофор».

Попросите учащихся показать карточками сигналы, обозначающие их понимание или непонимание материала, затем задайте вопросы в соответствии с тем, какие карточки подняты учащимися. По итогам полученных ответов примите решение о повторном изучении, закреплении темы или продолжении изучения материала по программе.

Домашнее задание.  Обязательное домашнее задание по цели обучения 6.5.2.10 по теме: «Исследование зависимостей между величинами, используя графики реальных процессов» предполагает количество заданий, на выполнение которых учащиеся должны затрачивать не более 15-20 минут. Задания для выполнения дома рекомендуем дифференцировать по уровню сложности, включая задания на анализ, синтез и оценку. При этом, желательно, давать учащимся задачи практического содержания: решить из уровня В учебного пособия «Математика 6» №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.