7. Методические рекомендации к проведению урока

Методические рекомендации к проведению урока.

Тема урока: Модуль числа.

Цели обучения: 6.3.3.1 находить расстояние между точками на координатной прямой.

Цели урока: - формировать понятие о модуле числа как расстоянии точки,          

                          соответствующей данному числу до начала отсчета;

                       - находить рассяние между точками на координатной прямой.

Критерии оценивания: - использует геометрический смысл модуля;

                                     - вычисляет расстояние между точками на координатной прямой.

Организационный момент, очень кратковременный, определяет весь психологический настрой урока. Психологический настрой проводится для создания благоприятной рабочей обстановке в классе, чтобы дети поняли, что им рады, их ждали.

Приветливые, доброжелательные слова учителя, спокойная, уверенная манера являются условием выполнения задач данного этапа. Также можно рассказать притчу:
"Жил мудрец, который знал все. Один человек захотел доказать, что мудрец знает не все. Зажав в ладонях бабочку, он спросил: "Скажи, мудрец, какая бабочка у меня в руках: мертвая или живая?” А сам думает: "Скажет живая – я ее мертвлю, скажет мертвая – выпущу”. Мудрец, подумав, ответил: "Все в твоих руках”. 

Постановка темы и цели обучения, знакомство с критериями оценивания.

Постановка целей – не самый любимый и очень трудоемкий этап в деятельности педагога по подготовке к уроку. Этап целеполагания - основополагающий на уроке, так позволяет учителю видеть план и результат своего воздействия на умы учеников.

Цели должны быть: реальны, достижимы, конкретны, т.е. контролируемы; сформулированы продуктивно, т.е. «от ученика», с прогнозированием образовательного результата; соотносимы с типом и содержанием урока; личностно ориентированы.

Актуализация знаний.

Цель: актуализация знаний по теме "противоположные числа" и "координатная прямая"

Учащиеся просматривают видео – ролик https://www.youtube.com/watch?v=dRE57K77T0c (видеоресурс1).

После просмотра рекомендуется проведения самостоятельной работы, т.е. можете предложить учащимся решить уравнения с модулем

Проверка решения. Обсуждение с учащимися общей модели решения уравнений такого вида.

Объяснение нового материала и отработка навыков.

Цель: используя геометрический смысл модуля числа находить расстояние между точками на координатной прямой.

- Сегодня мы познакомимся с новым понятием – расстояние между точками на координатной прямой.

Просмотр видеоурока: https://www.youtube.com/watch?v=GLmU9DFFC5M (видеоресурс2)

Познакомьте учащихся с правилами нахождения расстояния между точками на координатной прямой. Попросите учащихся привести несколько примеров.

На основании слайдов №4-8, учащиеся совместно с учителем делают вывод, что

Расстояние между точками a и b  равно модулю разности координат этих точек.

            ρ(a; b)=|a-b|

Попробуйте вместе выполнить несколько устных заданий. Сделайте вывод.

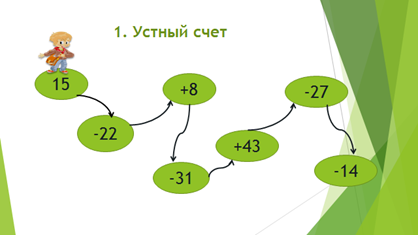
2. Устно решите задание с помощью координатной прямой: сколько целых чисел заключено между числами:                              Ответы: а) 10;

                        а) –8,9 и 2                                                        б) 8;

                        б) –10,4 и –3,7                                                 в) 6.

                        в) –1,2 и 4,6?

3. Найдите  расстояния между точками на координатной прямой:  

р(-6; 2) =

р(6; 3) =

р(0; 7) =

р(1; -4) =

Ответы:

р(-6; 2) = 8

р(6; 3) = 3

р(0; 7) = 7

р(1; -4) = 5

4. Найдите  расстояния между точками на координатной прямой:

р(2; -6) =

р(3; 6) =

р(7; 0) =

р(-4; 1) =

Ответы:

р(2; -6) = 8

р(3; 6) = 3

р(7; 0) = 7

р(-4; 1) = 5

Тренировочная работа. Проверь соседа.

Работайте вместе, внимательно все записываем в тетрадь.

Найдите ρ(х; у), если:

1) x = –14, у = –23;

Ответ: ρ(х; у)=|х–у|=|–14–(–23)|=|–14+23|=|9|=9

2) x = 5,9, у = –6,8;

Ответ: ρ(х; у)=|5,9–(–6,8)|=|5,9+6,8

Для запоминание и развития академической печи рекомендуется проведение математического диктанта «Продолжи предложение…».

u  Продолжить предложение

1. Координатная прямая – это прямая с указанными на ней …

2. Расстояние между двумя точками - это …

3. Противоположные числа – это числа, …

4. Модулем  числа Х называют …

5. Сравните значения выражений 

       a – b  V  b – a   сделайте вывод …

6. Сравните значения выражений 

      |a – b| V | b – a|  cделайте вывод …

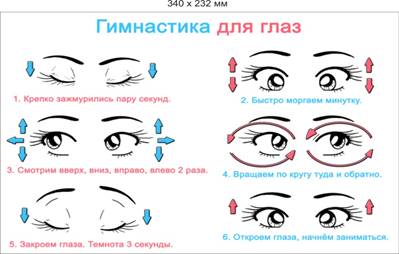
Физкультминутка. Физкультминутка (ФМ) способствует снятию локального утомления. По содержанию ФМ различны и предназначаются для конкретного воздействия на ту или иную группу мышц или систему организма в зависимости от самочувствия и ощущения усталости.

Физкультминутки проводятся во время уроков и состоят из 2-3 упражнений, направленных на снятие напряжения мышц спины, пальцев рук, плечевого пояса, органов зрения.

Закрепление.

Учащиеся выполняют тест (Приложение 1).

Взаимопроверка. Ученики обмениваются своими тестами и выполняют проверку правильности ответов.

Формативное оценивание.

Парная работа. Объедините учащихся в пары и предложите расшифровать имя наставника Ходжи Ахмеда Яссави.

Предоставьте каждой паре карточку с заданиями.

Например:

Дано: ; ; ; ; ; ; ; ; .

Найдите расстояние между точками.

1) А и С; 3) В и F; 5) В и G; 7) Е и К; 9) F и G;

2) D и F; 4) С и О; 6) О и Е; 8) А и D; 10) G и К.

Код ответов:

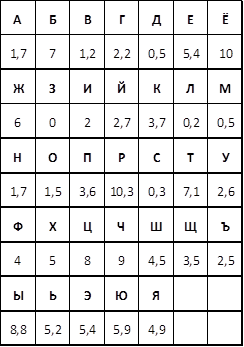
По окончании работы познакомьте учащихся с исторической справкой.

Ответ: АРЫСТАНБАБ.

Задание на дом: Ученик на выбор из дидактического материала выбирает уровень сложности для выполнения домашнего задания (Приложение 2)..

Рефлексия

Дерево успеха. Каждый листочек имеет свой определенный цвет: зеленый — все сделал правильно, желтый — встретились трудности, красный — много ошибок. Каждый ученик наряжает свое дерево соответствующими листочками. Подобным же образом можно наряжать елку игрушками, украшать поляну цветами и т.д

Учебник Математика 6 класс А.П. Ершова, В.В. Голобородько (2013 год) Самостоятельные и контрольные работы

Скачано с www.znanio.ru