76 Решение текстовых задач Методические рекомендации к уроку

Методические рекомендации к уроку

Тема урока "Решение текстовых задач."

Цели обучения:

6.5.2.4

составлять выражения с переменными и формулы при решении текстовых задач;

6.2.1.10

выражать из равенств одни переменные через другие.

Критерии оценивания:

Учащийся:

знает:

·         как составлять выражения с переменными;

·         формулы при решении текстовых задач;

умеет:

·         составлять математические модели при  решении текстовой задачи;

·         выражать из равенств одни переменные через другие.

Теоретический материал:

1.      Изучить условие задачи, если надо, сделать чертёж.

2.      Выяснить, о каких величинах идет речь в задаче.

3.      Выбрать любую из этих величин для составления выражения по условию задачи.

4.      Установить, каким действием и над какими величинами можно получить выражение.

5.      Выяснить, какие из них известны, какие нет. Ввести обозначение переменной.

6.      Записать выражение или уравнение.

7.      Найти числовое значение выражения, если даны значения переменной или решить уравнение.

8.      Записать ответ, правильно выбирая единицы измерения.

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание.

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Индивидуальная работа. Для проверки оценки усвоения пройденного материала предложить задания из Приложения 1.

Приложение 1

Работа с классом. С учащимися в активном диалоге разобрать пункты действий при решении текстовых задач, предварительно составляя выражения.

Задача. В одном бидоне молока в 3 раза больше, чем в другом. Когда из одного бидона перелили в другой 5 литров, молока в бидонах стало поровну. Сколько литров молока было в каждом бидоне первоначально?

Решение:

Сначала введём переменную, с помощью которой обозначим неизвестную нам величину, которую необходимо найти по условию задачи.

Пусть x л — количество молока, которое было до переливания во втором бидоне.

Тогда в первом бидоне его было 3x л.

После переливания в первом бидоне осталось (3x –5) л молока, а во втором стало (x+5) л.

По условию задачи известно, что после переливания в обоих бидонах молока стало поровну. Составим уравнение: 3x –5=x+5.

Для решения задачи надо:

1.      Изучить условие задачи, если надо, сделать чертёж.

2.      Выяснить, о каких величинах идет речь в задаче.

3.      Выбрать любую из этих величин для составления выражения по условию задачи.

4.      Установить, каким действием и над какими величинами можно получить выражение.

5.      Выяснить, какие из них известны, какие нет. Ввести обозначение переменной.

6.      Записать выражение или уравнение.

7.      Найти числовое значение выражения, если даны значения переменной или решить уравнение.

8.      Записать ответ, правильно выбирая единицы измерения.

Выполнить упражнения из Приложения 2.

Приложение 2

Составить выражение по условию задачи, упростить и найти значение:

1) Из листа железа со сторонами а см и b см вырезали по углам 4 одинаковых квадрата со стороной 4 см. Чему равен периметр оставшейся части? Решить задачу при а = 20 см;
b = 30 см.

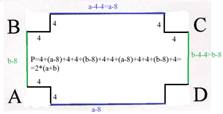
Составить выражение по условию задачи, упростить и найти значение:

2)  Из прямоугольного листа железа со сторонами х см и у см вырезали два квадратных отверстия со стороной 6 см. Найти площадь оставшейся части. Решить задачу при х = 18; у = 24.

Решение:

S - площадь оставшейся части

S = x ∙ y - 6² ∙ 2

S = 18 ∙ 24 - 6² ∙ 2 = 432 - 72 = 360 см² - площадь оставшейся части

Ответ: 360 см².

Составить выражение по условию задачи:

3) В одном бидоне — a л, а в другом — b л молока. На сколько литров молока во втором бидоне больше, чем в первом?

A).  a+b

B).  a−b

C).  b−6

D).  a+6

E).   b−a

4) Составь уравнение к задаче, начало решения которой выглядит так:

Известно, что число стульев, оставшихся в кабинетах, было одинаковым.

Найди число стульев, которые были в 1-м кабинете.

5) Обозначьте одну неизвестную величину буквой х, выразите через х другую неизвестную величину, составьте уравнение по условию задачи:

Задача. На одной автостоянке было в 5 раз меньше машин, чем на другой. Когда со второй стоянки на первую перевели 120 автомобилей, машин на стоянках стало поровну. Сколько машин было на каждой стоянке первоначально?

Групповая работа. Для выполнения упражнений разделите учащихся на малые группы, для того чтобы они обсудили задание и выполнили его совместно. При выполнении задания учащиеся анализируют условие, в ходе обсуждения развивают математическую речь, самостоятельно принимают решение, развивают навыки работы в команде. Наблюдайте за работой учащихся, если необходимо корректируйте их деятельность. По окончании времени каждая группа представляет свою работу классу.

Приложение 3

Обозначьте одну неизвестную величину буквой х, выразите через х другую неизвестную величину, составьте уравнение по условию задачи и ответьте на вопрос задачи, решив уравнение.

Задача 1) Автобус и грузовая машина, скорость которой на 19 км/ч больше скорости автобуса, выехали одновременно навстречу друг другу из двух городов, расстояние между которыми — 715 км. Найди скорости автобуса и грузовой машины, если известно, что они встретились через 5 ч. после выезда.

Решение:

Скорость автобуса х

скорость грузовой х+19

х+х+19 - скорость сближения

715 : 5 = 143 (км/ч) скорость сближения

(х+х+19)∙5=715 (км) расстояние между городами

х+х+19=143

2х=143-19

2х=124

х=62

62 км/ч скорость автобуса

62+19=81 км/ч скорость грузового

Ответ: 62 км/ч, 81 км/ч.

Задача 2) У двух братьев поровну орехов. Если старший брат отдаст младшему 20 орехов, то орехов у него станет в 5 раз меньше, чем у младшего. Сколько орехов у каждого брата было первоначально?

Задача 3) В первом бидоне в 3 раза больше молока, чем во втором. Если из первого перелить 20 л во второй, то молока в бидонах будет поровну. Сколько литров молока в каждом бидоне?

Задача 4) На двух полках стояли книги. На первой — в 2 раза больше, чем на второй. Сколько книг стояло на каждой полке, если на первой их было на 12 больше, чем на второй?

Задача 5) В булочную привезли 654 кг чёрного и белого хлеба. После того как продали 215 кг чёрного и 287 кг белого хлеба, того и другого сорта осталось поровну. Сколько чёрного и белого хлеба в отдельности привезли в булочную?

Учитель проходит по рядам, слушает, при необходимости корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям

Каждая группа демонстрирует свой результат выполнения задания..

Старший группы оценивает вклад каждого, выставляя отметку.

Беседа. Рефлексия.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости). Ученики, распределяя в паре задания или в группе, самостоятельно выбирают уровень сложности. Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат решения задачи, записывать, а также решать задания на упрощение выражений, опираясь на ранее изученные правила и способы упрощения выражений и решение уравнений. Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

"Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

"Математика 6", Алдамуратова Т.А, Байшоланов Т.С.;

Математика 6 класс Виленкин

Самостоятельные и контрольные работы, Ершова А.П., Голобородько В.В.