Adiabatic process, Poisson equation Text

Text for the individual work.

Information from the site:

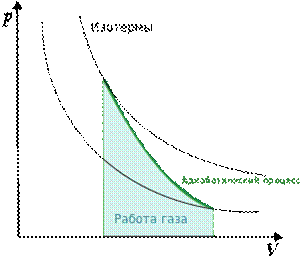
The Poisson equation describes an adiabatic process occurring in an ideal gas. An adiabatic process is a process in which there is no heat exchange between the system under consideration and the environment. Q = 0

The Poisson equation has the form:

Here V – the volume occupied by a gas, p is its pressure, and k (γ) – value, which is called the adiabatic index.

The adiabatic index in the Poisson equation

The adiabatic index can be calculated as the ratio of the isobaric heat capacity of the gas to its isochoric heat capacity:

In practical calculations it is convenient to remember that for an ideal gas the adiabatic index is equal to , for diatomic – , and for triatomic – .

What about real gases when the forces of interaction between molecules start to play an important role? In this case, the adiabatic index for each test gas can be obtained experimentally. One such method was proposed in 1819 by Clement and Dezorm. We fill the balloon with cold gas until it reaches pressure. Then we open the valve, the gas begins to adiabatically expand, and the pressure in the cylinder drops to atmospheric. After the isochoric gas has warmed to ambient temperature, the pressure in the cylinder will rise to. Then the adiabatic index can be calculated by the formula:

The adiabatic index is always greater than 1, therefore, with adiabatic compression of the gas — both ideal and real — the gas temperature always rises to a smaller volume, and when expanded, the gas cools.This property of the adiabatic process, called the pneumatic flint, is used in diesel engines, where the combustible mixture is compressed in a cylinder and ignited by heat. Let us recall the first law of thermodynamics: Q = ΔU + A, where ΔU is the internal energy of the system, and A is the work performed on it. Since Q = 0, the work carried out by the gas, goes only to change its internal energy - and hence the temperature. From the Poisson equation, you can obtain a formula for calculating the gas operation in an adiabatic process:

Here n is the amount of gas in moles, R is the universal gas constant, T is the absolute temperature of the gas.

The Poisson equation for the adiabatic process is used not only in the calculations of internal combustion engines, but also in the design of refrigeration machines.

It is worth remembering that the Poisson equation accurately describes only an equilibrium adiabatic process consisting of continuously changing equilibrium states. If, in reality, we open the valve in the cylinder so that the gas expands adiabatically, a non-stationary transient process will appear with gas turbulence, which will damp out due to macroscopic friction.

The real process can be considered adiabatic if it proceeds very quickly and does not have time to carry out heat exchange with the environment.