алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Итоги контрольной работы - Урок 4 - Уравнения и неравенства. Системы уравнений и неравенств

Цели: сообщить результаты работы; рассмотреть наиболее типичные ошибки; разобрать трудные задачи.

Ход урока

I. Сообщение темы и целей урока

II. Итоги контрольной работы

III. Ответы и решения

Ответы

Вариант 1

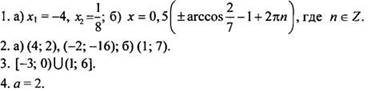
Вариант 2

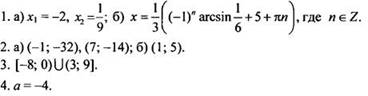
Вариант 3

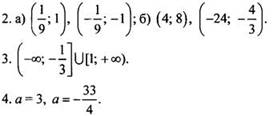
Вариант 4

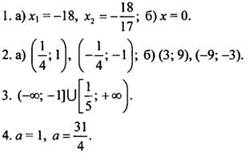
Решения

Вариант 5

1. а) Запишем уравнение в виде  Учтем определение модуля |а| = -а, если а ≤ 0. Тогда данное уравнение равносильно квадратному неравенству х² + 5х - 14 ≤ 0. Его решение: х ∈ [-7; 2].

Ответ: [-7; 2].

б) Перенесем все члены уравнения в левую часть, учтем его ОДЗ (х ≤ -3) и разложим эту часть на множители:  Произведение множителей равно нулю, если один из них равен нулю, а другие имеют смысл. Получаем два случая:

а) 2х - 1 =0. Корень этого линейного уравнения х = 1/2 не входит в ОДЗ (посторонний корень);

б)  или -х - 3 = 1, откуда х = -4.

Ответ: х = -4.

2. а) Систему уравнений запишем в виде  Для решения используем способ подстановки. Из первого уравнения выразим х = 3 - у² и подставим во второе: (3 - у²)² - 2у⁴ = 2 или 0 = у⁴ + 6у² - 7. Корни этого биквадратного уравнения: у = ±1 (тогда х = 2). Итак, система уравнений имеет два решения: (2; 1), (2; -1).

Ответ: (2; 1), (2; -1).

б) В первом уравнении системы перейдем к одному основанию логарифмов:  Введем новую переменную t = log_xy и получим уравнение:  или t² – 4t + 4 = 0, или (t - 2)² = 0, которое имеет единственный корень t = 2. Вернемся к старой переменной log_xy = 2, откуда у = х². Подставим эту величину во второе уравнение: 5√х - х = 4 (учтено, что х > 0, x ≠ 1). Введем новую переменную z = √х и получим уравнение: 5z - z² = 4 или 0 = z² - 5z + 4. Корни этого уравнения: z = 1 (не подходит) и z = 4. Вернемся к старой переменной √х = 4 и найдем х = 16 и у = 16² = 256. Система имеет единственное решение (16; 256).

Ответ: (16; 256).

3. Введем новую переменную t = log₂x и получим рациональное неравенство:  или  или  Решая это неравенство методом интервалов, найдем: t ≤ -1 и 1 < t ≤ 2. Вернемся к старой переменной и получим простейшие логарифмические неравенства: log₂х ≤ -1 и 1 < log₂х ≤ 2, откуда 0 < х ≤ 1/2 и 2 < х ≤ 4.

Ответ: 

4. Рассмотрим график функции у = sin х на отрезке [0; 2π].

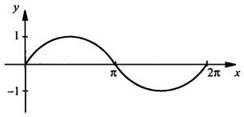
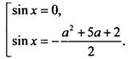Перенесем все члены уравнения в правую часть и разложим ее на множители:  Это уравнение равносильно совокупности уравнений  Первое уравнение на отрезке [0; 2π] уже имеет 3 корня. Значит, второе уравнение на данном отрезке должно иметь единственный корень. Это возможно, если правая часть уравнения будет равна ±1. Получаем совокупность уравнений: 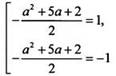 или  которая имеет четыре решения: а = -1, а = -4, а = 0, а = -5.

Ответ: а = -1, а = -4, а = 0, а = -5.

Вариант 6

1. а) Запишем уравнение в виде  Учтем определение модуля |а| = -а, если а ≤ 0. Тогда данное уравнение равносильно квадратному неравенству х² - 5х - 15 ≤ 0. Его решение: х ∈ [-3; 5].

Ответ: [-3; 5].

б) Перенесем все члены уравнения в левую часть, учтем его ОДЗ (х ≤ -1) и разложим эту часть на множители:  Произведение множителей равно нулю, если один из них равен нулю, а другие имеют смысл. Получаем два случая:

а) х - 2 = 0. Корень этого линейного уравнения х = 2 не входит в ОДЗ (посторонний корень);

б)  или -х - 1 = 1, откуда х = -2.

Ответ: х = -2.

2. а) Систему уравнений запишем в виде  Для решения используем способ подстановки. Из первого уравнения выразим х = у² - 2 и подставим во второе: 2у⁴ - (у² - 2)² = 1 или у⁴ + 4у² - 5 = 0. Корни этого биквадратного уравнения у = ±1 (тогда х = -1). Итак, система уравнений имеет два решения: (-1; 1), (-1; -1).

Ответ: (-1; 1), (-1; -1).

б) В первом уравнении системы перейдем к одному основанию логарифмов:  Введем новую переменную t = log_xу и получим уравнение:  или 2t² – 5t + 2 = 0, которое имеет корни t₁ = 2 и t₂ = 1/2. Вернемся к старой переменной: log_xy = 2 (откуда у = х²) и log_xу = 1/2 (тогда у = √х). Подставим эти величины во второе уравнение и рассмотрим два случая:

 Из второго уравнения имеем: 3√x - x = 2 (учтено, что х > 0, х ≠ 1). Введем новую переменную z = √х и получим уравнение 3z - z² = 2 или 0 = z² - 3z + 2. Корни этого уравнения: z = 1 (не подходит) и z = 2. Вернемся к старой переменной √х = 2 и найдем: х = 4 и у = 4² = 16.

 Из второго уравнения имеем:  Введем новую переменную  и получим уравнение: 3z² - z = 2 или 3z² - z - 2 = 0. Корни этого уравнения: z = 1 (не подходит) и z = -2/3 (не подходит, т. к. z ≥ 0).

Система имеет единственное решение (4; 16).

Ответ: (4; 16).

3. Введем новую переменную t = log₂х и получим рациональное неравенство  или  или  Решая это неравенство методом интервалов, найдем: -2 ≤ y < -1 и t ≥ 1. Вернемся к старой переменной и получим простейшие логарифмические неравенства: -2 ≤ log₂х < -1 и log₂х ≥ 1, откуда  и х ≥ 2.

Ответ: 

4. Рассмотрим график функции у = sin x на отрезке [0; 2π].

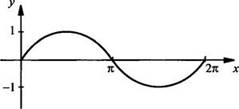
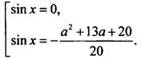Перенесем все члены уравнения в правую часть и разложим ее на множители:  Это уравнение равносильно совокупности уравнений  Первое уравнение на отрезке [0; 2π] уже имеет три корня. Значит, второе уравнение на данном отрезке должно иметь один корень. Это возможно, если правая часть уравнения будет равна ±1. Получаем совокупность уравнений: 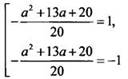 или  которая имеет четыре решения: а = -8, а = -5, а = 0, а = -13.

Ответ: а = -8, а = -5, а = 0, а = -13.