алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Итоги контрольной работы - Степени и корни. Степенные функции

Цели: сообщить результаты работы; рассмотреть наиболее типичные ошибки; разобрать трудные задачи.

Ход урока

I. Сообщение темы и целей урока

II. Итоги контрольной работы

III. Ответы и решения

Ответы

Вариант 1

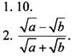
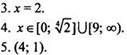
6. Второе число больше.

Вариант 2

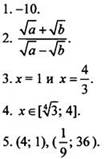
6. Первое число больше.

Вариант 3

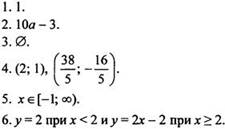
Вариант 4

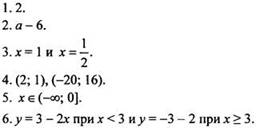
Решения

Вариант 5

1. Используем свойства корней и формулу разности квадратов. Получаем: 

Ответ: 3.

2. Приведем дроби к общему знаменателю и упростим:

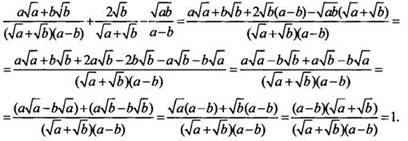
Ответ: 1.

3. Для решения уравнения  введем новые переменные  Запишем первое уравнение: a - b = 1. Возведем в куб новые переменные a³ = 24 + √x и b³ = 5 + √х. Вычтем эти равенства друг из друга и получим второе уравнение: а³ – b³ = 19 или  откуда (с учетом первого уравнения) a² + ab + b² = 19. Получаем систему уравнений  Подставим первое уравнение во второе:  или b² + b - 6 = 0. Корни этого уравнения b₁ = 2 и b₂ = -3. Вернемся к старой переменной. Получаем уравнения: 2³ = 5 + √х (корень х = 9) и (-3)² = 5 + √х (корней не имеет).

Ответ: x = 9.

4. Для решения системы уравнений  введем новые переменные  Запишем первое уравнение: а + b = 3. Найдем квадраты новых переменных: а² = 2х - 1 и b² = у + 3 и перемножим их: а²b² = 2ху = у + 6х - 3, откуда а²b² + 3 = 2xу – у + 6х. Можно записать второе уравнение: a²b² + 3 = 7, откуда ab = 2 (учтено, что а, b ≥ 0). Получаем систему уравнений:  решение которой a₁ = 1, b₁ = 2 и а₂ = 2, b₂ = 1. Вернемся к старым переменным. Имеем две системы уравнений:  (решение х = 1, у = 1) и  (решение х = 5/2, у = -2).

Ответ: (1; 1), (5/2; -2).

5. Область определения функции х ≥ -2. Введем переменную  тогда х = z² - 2. Функция имеет вид  или y = |z - 1| - (z + 1). Раскроем знак модуля. При z < 1 (т. е.  или х < -1) получаем:  при z ≥ 1 (т. е. х ≥ -1) имеем: у = -2. Построим этот график.

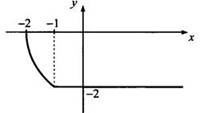
Ответ: см. график.

6. Напомним формулу куба суммы  Обозначим сумму:  и возведем ее в куб:  или x³ = 40 + 6х. Для нахождения х получили кубическое уравнение х³ - 6х - 40 = 0, которое имеет один действительный корень х = 4 (натуральное число).

Ответ: доказано.

Вариант 6

1. Используем свойства корней и формулу разности квадратов. Получаем: Ответ: 2.

2. Используем формулу суммы кубов, приведем дроби к общему знаменателю и упростим: 

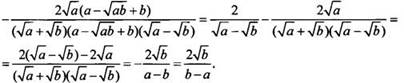
Ответ: 

3. Для решения уравнения  введем новые переменные  Запишем первое уравнение: a + b = 4. Возведем в куб новые переменные:  и  Сложим эти равенства и получим второе уравнение а³ + b³ = 16 или  откуда (с учетом первого уравнения) а² – аb + b² = 4. Получаем систему уравнений  Подставим первое уравнение во второе:  или а² - 4а + 4 = 0. Корень этого уравнения а = 2. Вернемся к старой переменной. Получаем уравнение:  или . Корень этого уравнения х = 0.

Ответ: х = 0.

4. Для решения системы уравнений  введем новые переменные  Запишем первое уравнение: а + b = 3. Найдем квадраты новых переменных: а² = 2 - х и b² = 5 - у и перемножим их: а²b² = 10 - 5х - 2у + ху, откуда 5х + 2у - ху = 10 - а²b². Можно записать второе уравнение: 10 - а²b² = 6, откуда ab = 2 (учтено, что а, b ≥ 0). Получаем систему уравнений  решение которой а₁ = 1, b₁ = 2 и а₂ = 2, b₂ = 1. Вернемся к старым переменным. Имеем две системы уравнений:  (решение х = 1, у = 1) и  (решение х = -2, у = 4).

Ответ: (1; 1), (-2; 4).

5. Область определения функции х ≥ -1. Введем переменную  тогда х = z² - 1. Функция имеет вид:  или y = z + 1 + |z - 1|. Раскроем знак модуля. При z < 1 (т. е.  или х < 0) получаем у = 2, при z ≥ 1 (т. е. х ≥ 0) имеем:  Построим этот график.

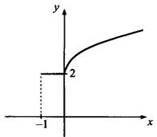
Ответ: см. график.

6. Напомним формулу куба суммы:  Обозначим сумму:  и возведем ее в куб:  Для нахождения х получили кубическое уравнение х³ - 3х - 18 = 0, которое имеет один действительный корень х = 3 (натуральное число).

Ответ: доказано.