Поделиться
Алгебра 9 класс Тригонометрия Формулы сложения Повторение.pdf
И.В.Яковлев | Материалы по математике | MathUs.ru
Формулы двойного угла — это формулы, выражающие тригонометрические функции угла 2α через тригонометрические функции угла α. Все формулы двойного угла выводятся из соответствующих формул сложения.
Исходим из формулы синуса суммы:
sin(α + β) = sinαcosβ + cosαsinβ. Полагаем в этой формуле β = α:
sin(α + α) = sinαcosα + cosαsinα,
|
то есть |
|
|
sin2α = 2sinαcosα. Мы получили формулу синуса двойного угла. Косинус двойного угла Исходим из формулы косинуса суммы: cos(α + β) = cosαcosβ − sinαsinβ. Полагаем в этой формуле β = α: cos(α + α) = cosαcosα − sinαsinα, то есть |
(1) |
|
cos2α = cos2 α − sin2 α. |
(2) |
Это — первая формула косинуса двойного угла. Имеются ещё две. Они получаются из формулы (2) с помощью основного тригонометрического тождества.
Так, согласно основному тригонометрическому тождеству имеем: cos2 α = 1 − sin2 α. Подставляя это в (2), получим:
cos2α = 1 − 2sin2 α. (3)
С другой стороны, имеем также: sin2 α = 1 − cos2 α. Подставляем это в (2):
cos2α = 2cos2 α − 1. (4)
Как видите, в отличие от синуса двойного угла, где имеется одна-единственная формула, здесь нужно знать три формулы косинуса двойного угла (2)–(4).
Берём формулу тангенса суммы:
.
Полагаем в ней β = α и получаем формулу тангенса двойного угла:
(5)
Точно так же из формулы котангенса суммы:
получим:
Мы переходим к формуламполовинногоугла, которые связывают тригонометрические функции угла α и тригонометрические функции угла α/2. По сути это те же формулы двойного угла, только записанные несколько иным образом.
По формуле (3) косинуса двойного угла имеем:
,
откуда
(6)
А теперь точно так же воспользуемся формулой (4):
,
откуда
(7)
Тождества (6) и (7) называются формуламипонижениястепени. Название понятно: в левой части каждой формулы стоит квадрат тригонометрической функции, а в правой части — первая степень косинуса.
Взяв отношение равенств (6) и (7), получим:
Данная формула, как видите, выражает квадрат тангенса половинного угла. Имеются также две формулы, выражающие сам тангенс.
Первая формула:
Чтобы доказать это тождество, возьмём его правую часть и путём преобразований выведем из неё левую часть. Используем формулы (6) и (1).
.
Вторая формула:
Докажите её самостоятельно, используя формулы (1) и (7).
Оказывается, любую тригонометрическую функцию угла α можно выразить через тангенс половинного угла α/2.
1. Формула для синуса:
(8)
Доказываем «справа налево»,
умножая числитель и знаменатель дроби на 
:
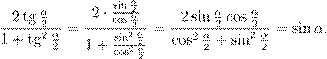
2. Формула для косинуса:
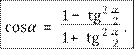(9)
Попробуйте доказать её самостоятельно. Приём тот же:
умножаем числитель и знаменатель на 
. Но в данном случае
вместо формулы синуса двойного угла вам понадобится формула (2) косинуса двойного угла.
3. Формула для тангенса — это уже известная нам формула (5):
(10)
4. Формула для котангенса — это «перевёрнутая» формула (10):
(11)
Формулы (8)–(11) называются универсальной подстановкой.
1. Вычислите:
а)
2sin15◦ cos15◦; б)
;
в)
4sin75◦ cos75◦; г)
;
д)
; е)
.
2. Вычислите:
а)
cos2 15◦ −
sin2 15◦; б)
;
в)
2cos2 75◦ −
1; г) 
;
д)
; е)
2sin2 165◦ −
1.
3. Упростите выражение:
а)
б)
в)
; г)
;
д)
; е)
.
|
4. Упростите выражение: |
|
|
а) sin2α + (sinα − cosα)2 ; |
б) sin2αctgα − 1; |
в)
; г)
;
д) (cos3α + sin3α)(cos3α − sin3α); е) 1 − 2sin2 4x.
5.
Известно, что 
. Найдите sin2α
и cos2α.
6.
Известно, что 
и 
. Найдите sin2α и cos2α.
7. В равнобедренном треугольнике синус угла при основании равен 1/3. Найдите косинус угла при вершине этого треугольника.
8.
Вычислите 
.
9. Упростите выражение:
а)
; б)
;
в)
; г)
;
д) (1 − tg2 α)cos2
α; е) 
.
|
10. Докажите тождество: |
|
|
а) (cosα + sinα)2 = 1 + sin2α; |
б) cos4 α − sin4 α = cos2α; |
в)
ctgα − sin2α
= ctgαcos2α; г)
;
д) sin2α − tgα = cos2αtgα; е) (ctgα − tgα)sin2α = 2cos2α;
ж)
(1 + cos2α)tgα =
sin2α; з) 
;
и) 
1; к)
;
л)
; м)
;
н) 
; о) 
11.
Найдите sin2α,
если 
.
12. Докажите тождество:
.
13. Докажите тождество:
а)
; б)
14. Выведите формулы тройного угла:
а) sin3α = 3sinα − 4sin3 α;
б) cos3α = 4cos3 α − 3cosα;
в) 
.
15. Исходя из равенства cos54◦ = sin36◦, вычислите sin18◦.
16. Покажите, что:
а)
; б)
.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
