алгебра и начало анализа

                                     Тема «Сумма углов треугольника»

Цели урока:

Цели и задачи:

1.      С помощью эксперимента подвести детей к формулировке теоремы о сумме углов треугольника, доказать ее и научить применять полученные знания в решении задач.

2.      Развитие познавательной деятельности, мышления, внимания

3.      Содействовать достижению учащимися определенного уровня компетентности в сфере массовых коммуникаций.

4.      Развивать математическую речь учащихся;

5.      Формировать умение анализировать материал и делать выводы;

6.      Воспитывать: интерес к предмету, умение доводить дело до конца, уверенность в своих способностях в учебе.

Оборудование: компьютер, проектор, интерактивная  доска, карточки с планом практической работы,

            План урока.

1. Организационный момент.
2. Постановка учебной задачи.
3. Практическая работа «Сумма углов треугольника».
4. Доказательство теоремы о сумме углов треугольника.
5. Решение проблемной задачи.
6. Решение задач по готовым чертежам.
7. Подведение итогов урока.
8. Постановка домашнего задания.

Ответьте на следующий вопрос. Изучению какой геометрической фигуры мы уделяли больше всего внимания в 7 классе?

Как вы считаете, почему именно с треугольника мы начали изучение геометрии в 7 классе?

Треугольник – самая простая замкнутая прямолинейная фигура, свойства которой человек узнал еще в глубокой древности, так как эта фигура всегда имела широкое применение в практической жизни (строительстве и земледелии), любой многоугольник можно диагоналями разделить на треугольники.

Примеры различных треугольников. 

 Эмоциональное включение учащихся в урок.

Скульптура невозможного треугольника,в центре бельгийской деревни Опховен (слайд)

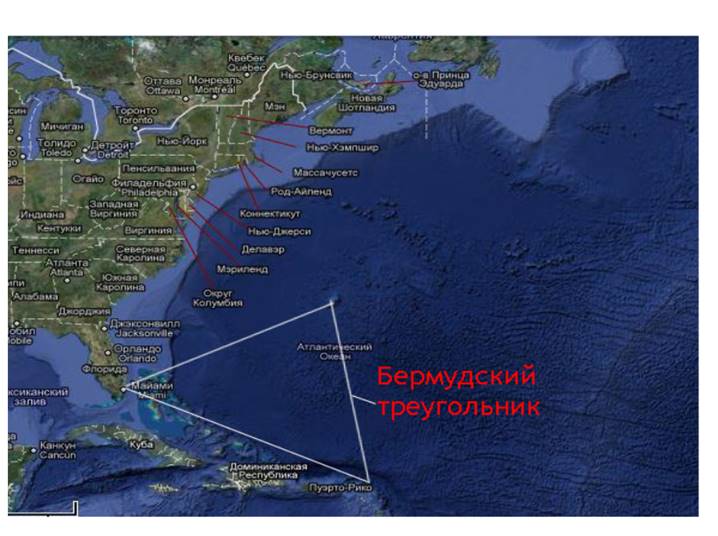
В Атлантическом океане есть место, по форме напоминающее геометрическую фигуру, о которой мы сегодня будем говорить. Это место, расположенное между Бермудскими островами, государством Пуэрто-Рико, полуостровом Флорида и называется «бермудским треугольником». А ещё его называют «дьявольский треугольник», «треугольник проклятых». Район является очень сложным для навигации: здесь большое количество отмелей, часто зарождаются циклоны и штормы.

Учитель: 

Ребята, сегодняшний урок мне хотелось бы начать с китайской мудрости:

«Скажи мне, и я забуду,

Покажи, и я запомню

Дай мне действовать самому,

И я научусь.»  (слайд 2)

Сегодня наш класс превратится в научно-исследовательский институт, а вы станете его сотрудниками. И мы не только познакомимся с работой научно-исследовательского института, но и сами будем делать открытия! НИИ – учреждение  для  проведения  научных   исследований.

И так: научно-исследовательский институт имеет подразделения:

1. Лаборатория экспериментов.

2.Лаборатория научных доказательств.

3. Лаборатория испытаний.

В  исследовании  важно  выдвинуть  гипотезу. Это  позволяет  конкретизировать  предмет  исследования. В ходе  работы, она  может быть  либо  подтверждена,  либо  опровергнута. Гипотеза сформулирована. Чтобы она стала истинной, её нужно доказать, убедиться, что она справедлива для любого треугольника.

2. Повторение. Проверка д/з.

На предыдущих уроках мы с вами изучали признаки параллельности прямых и свойства углов при параллельных прямых. И сегодня на уроке, полученные по этой теме знания, помогут сделать открытие.

Все дома изображали произвольный треугольник (по вариантам) и с помощью транспортира измеряли углы треугольников, записывали свои измерения и находили сумму углов треугольника. (слайд 5)

Что заметили? - Все суммы близки к 180°. Значит, сумма углов треугольника равна 180°.

Какие утверждения, связанные с этой величиной вам известны? (слайд 6)

Развернутый угол равен 180°.

Сумма смежных углов равна 180°.

Сумма односторонних углов при параллельных прямых равна 180°.

Сумма углов треугольника равна 180°.

Какому из этих утверждений нам приходится пока только верить, и нами еще не доказано?

Попробуйте определить цели урока. (доказать утверждение о сумме углов тр-ка, найти ему применение в задачах)

3. Изучение нового.

- Итак, ребята, у вас появилась гипотеза: сумма углов треугольника равна180° . Однако, у многих из вас получились результаты, близкие к 180°, но не 180°, Почему? Измеряя, мы получаем приближенные значения.

 Сумма углов треугольника была практическим путем установлена, вероятно, еще в Древнем Египте.

 Прокл утверждал, что доказательство этого факта было известно еще в V в. до н. э.

Направляемся в лабораторию экспериментов (слайд 7)

 Выдвинутую  гипотезу: сумма углов треугольника равна 180°  можно проверить еще одной практической работой:

1. Где еще сегодня называли это число? Величина развернутого угла.

·         На столах лежат  у каждого ученика вырезанные треугольники. Путем перегибания соберем углы треугольника в одну точку(слайд1).

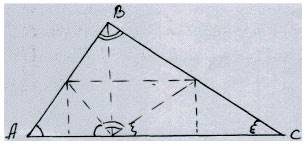
Работа парами: складываем так, чтобы углы треугольника собрались в одну точку. Проверьте себя(слайд3)

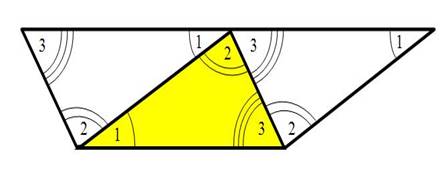
Гипотеза сформулирована. Чтобы она стала истинной, её нужно доказать, убедиться, что она справедлива для любого треугольника.

• Вырезать углы и сложить их вершинами вместе (разместить демонстрационный материал на магнитной доске).                                                                                             

Теперь  перейдем в лабораторию доказательств и здесь мы с вами докажем научно, что это действительно так!!! Используя готовый чертеж, докажите теорему о сумме углов треугольника (слайд 9)

1.Записываем формулировку нашего открытия – теорему «Сумма углов треугольника равна 180°».

2.Док-во: Попробуем доказать теорему, “собрав” все углы треугольника в одну вершину (на смарт-доске выполняется чертеж). “ Собрать углы” - значит, “ взять углы”, равные данным. (слайд 10)

ДАНО: АВС, 1,  2, 3 - внутренние.

ДОКАЗАТЬ:  1 + 2 + 3 = 180°.

ДОКАЗАТЕЛЬСТВО:

1) Проведем прямую а // АС, В принадлежит прямой а.

При вершине В получились 3 угла, которые в сумме составляют развернутый угол, т.е. 4,  2, 5

2)  5 + 2 + 4 = 180°. (развернутый угол)

3)  5 = 3 (внутренние накрест лежащие при а // АС и секущей ВС )

4 = 1(внутренние накрест лежащие при а // АС и секущей АВ)

4) Заменим в равенстве (*) 5 на  3 , 4  на 1 и получим 1 + 2 +3 = 180°. Ч.т.д.

5. Историческая справка.       Слайд

Теорема о сумме углов треугольника – одна из важнейших теорем геометрии. Ее доказательство приписывают древнегреческому математику Пифагору, который жил в 580-500 годах V века до н.э.(портрет)

1.      4.Закрепление

2.      Сейчас мы посетим  лабораторию испытаний (практическое применение)  (слайд 12 – 17)

3.      Устно решаем задачи (слайд12 – 15), письменно одну задачу двумя способами (слайд16)

4.      Самостоятельно  задачи №5-8

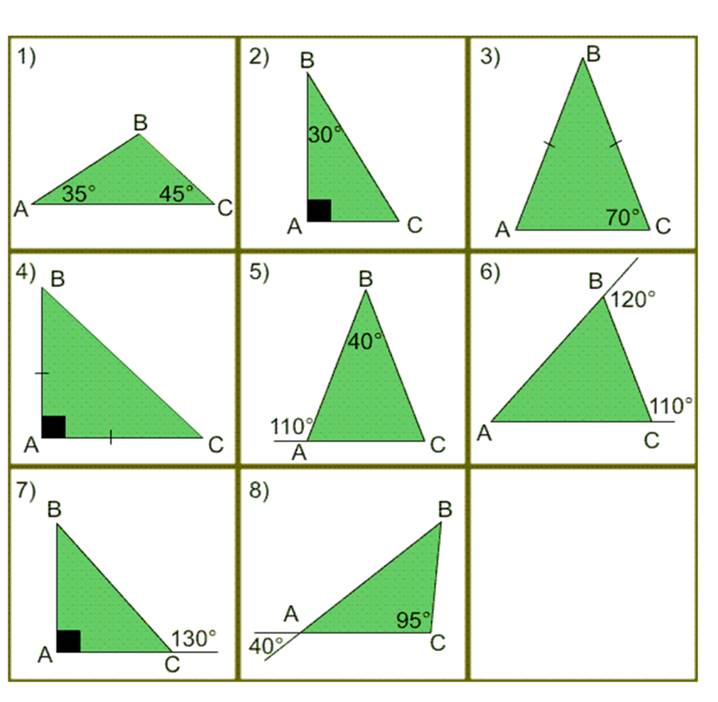
5.  Укажите номера верных утверждений:                                           Слайд 16.

а) Существует треугольник, у которого углы равны 120⁰, 30⁰ и 20⁰.

б) У прямоугольного треугольника все углы прямые.

в) Сумма углов треугольника равна  180⁰.

г) В тупоугольном треугольнике могут быть два тупых угла.

 6. Угол при вершине равнобедренного треугольника  на 30⁰ больше угла при основании. Найти углы

    треугольника.                                          

5.       Рефлексия

6.       

7.      Что нового для себя открыли на уроке?

8.      Предполагаемые ответы:

9.      Сегодня мы сделали научное открытие: сумма углов треугольника равна 180°.

10.  Мы узнали, как в жизни происходит открытие, т.е. как ученые делают открытия, их доказывают и находят применения своим открытиям.

11.   

12.  6.Подведение итогов урока: выставление оценок учащимся с обоснованием их, домашнее задание с комментариями

Скачано с www.znanio.ru